1. Конические зубчатые передачи Геометрия и кинематика

оси валов пересекаются под некоторым углом . Наиболее распространены передачи с углом .

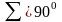Конические передачи сложнее цилиндрических в изготовлении и монтаже. Для нарезания конических колёс требуются специальные станки и специальный режущий инструмент ,необходимо выдерживать допуски на угловые размеры, а при монтаже обеспечивать совпадение вершин делительных конусов. Пересечение осей валов затрудняет размещение опор, В коническом зацеплении действуют осевые силы, которые усложняют конструкцию опор. Нагрузочная способность конической прямозубой передачи составляет лишь около 0,85 цилиндрической. Поэтому они применяются лишь по условиям компоновки механизмов, когда надо располагать валы под углом.

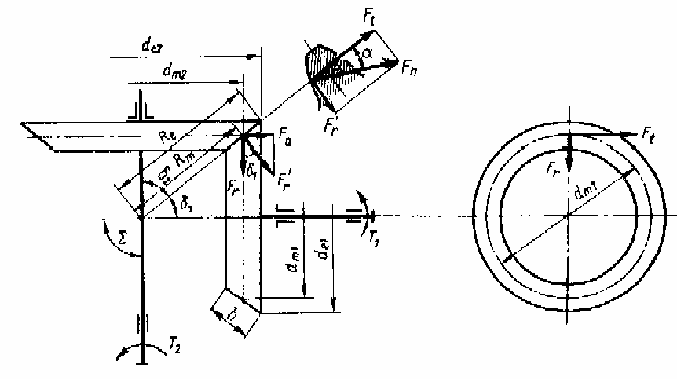
и 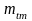- модули в сечении по наружному и среднему дополнительному конусам,

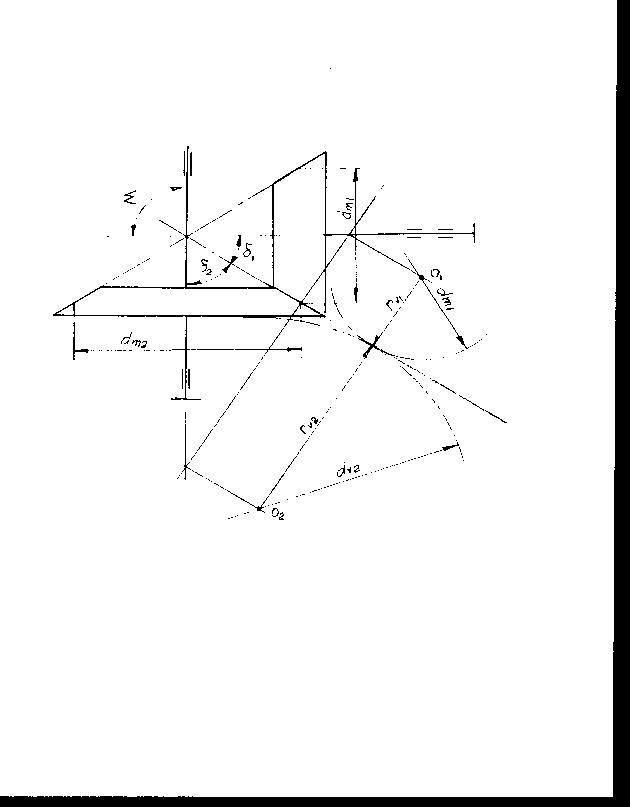
d_e и d_m – диаметры делительных (начальных) окружностей в сечении по наружному и среднему дополнительным конусам,

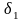и 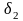- углы при вершинах делительных конусов шестерни и колеса,

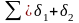- угол пересечения осей вращения зубчатых колёс (валов),

R_e и R_m – конусное расстояние и среднее конусное расстояние,

d_e = m_tez, d_m = m_tmz, z – число зубьев,

В чертежах задаются размерами в сечении по наружному дополнительному конусу, т.е. наибольшие. При этом m_te – величина стандартная.

Как и у цилиндрических колёс передаточное число u равно:

.

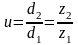2. Силы в прямозубой конической передаче.

В зацеплении конической передачи действуют силы:

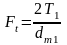- окружная (полезная, которая передаёт заданную нагрузку),

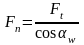- нормальная (общая) сила, действующая в зацеплении,

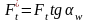- промежуточная, для определения других сил,

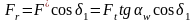- радиальная сила,

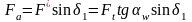- осевая сила.

3. Эквивалентные зубчатые колёса.

Эквивалентные зубчатые колеса - это прямозубые цилиндрическое зубчатые колёса, геометрические параметры которых используются при расчётах на прочность по контактным напряжениям и напряжениям изгиба. Форма зуба конического колеса в нормальном сечении дополнительным конусом такая же, как у эквивалентного колеса.

Диаметры эквивалентных колёс в среднем сечении дополнительным конусом

d_v1 = 2r_v1 = d_m1/cosδ₁; d_v2 = 2r_v2 = d_m2/cosδ₂.

d_v = m_tmz_v

здесь m_tm – модуль в среднем сечении,

z_v – число зубьев эквивалентных зубчатых колёс.

.

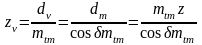Таким образом

и .

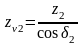4. Расчёт зубьев прямозубой конической передачи на изгиб.

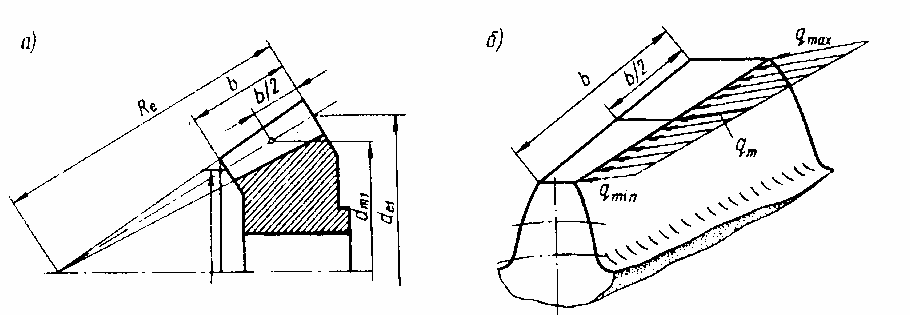
Удельная нагрузка q распределяется по закону треугольника, вершина которого также совпадает с вершиной делительного конуса. На основании этого доказывается, что напряжения изгиба одинаковы по всей длине зуба.

По аналогии с прямозубой цилиндрической передачей

,

гд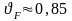е - опытный коэффициент, характеризующий понижение прочности прямозубой конической передачи по сравнению с цилиндрической при изгибе;

m_tm – модуль с среднем нормальном сечении зуба;

K_F – коэффициент расчётной нагрузки;

Y_F – коэффициент формы зуба