МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ

МАШИНОСТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ

(МАМИ)

Кафедра: “Системы автоматизированного проектирования”

Курсовая работа

по дисциплине:

“ Оптимизация технических объектов ”

Вариант №8

“Оптимальное проектирование вращающихся дисков машин“

Студент: Ефимов В.В.

Группа: М-47

Преподаватель: проф. Луганцев Л. Д.

Москва

2014 г.

Университет машиностроения

Кафедра «Системы автоматизированного проектирования»

ЗАДАНИЕ

на курсовую работу

«Оптимальное проектирование вращающихся дисков машин»

Конструктивная схема исследуемого диска машины представлена на рис.1.

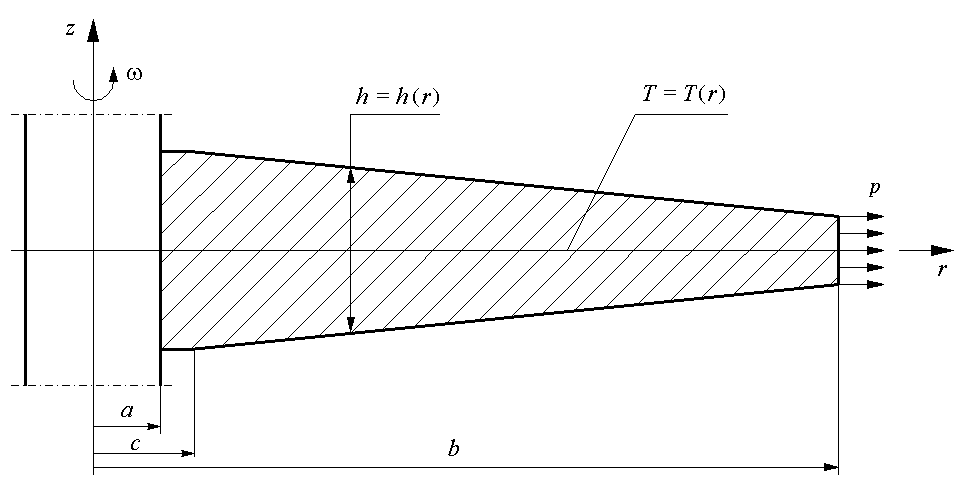
Рис.1. Конструктивная схема диска машины

Диск установлен на вал с натягом. Заданы геометрические размеры диска: a, b, c (рис.1). Рассматриваются диски с прямолинейным профилем (конические диски), а также гиперболические и экспоненциальные диски. Профиль исходной конструкции диска h = h(r) задан. Физико-механические характеристики материала диска и вала одинаковы. Плотность конструкционного материала  = 8000 кг/м³, коэффициент Пуассона  = 0,3. Модуль упругости и температурный коэффициент линейного расширения материала зависят от температуры:

,

.

Диск вращается с угловой скоростью  и нагрет до температуры T = T(r), переменной по радиусу и постоянной по толщине диска. Вал нагрет равномерно до температуры внутреннего контура диска. Интенсивность инерционной радиальной нагрузки, распределенной по наружной поверхности диска равна p. Числовые значения исходных данных представлены в табл. 1 и 2.

На первом этапе оптимального проектирования диска выполнить постановку и решение оптимизационной задачи. В результате решения задачи определить величину натяга, удовлетворяющую условиям:

• зазор между диском и валом в эксплуатационном режиме отсутствует,

• контактное давление между диском и валом в эксплуатационном режиме не превышает 0,1 МПа.

Определить также необходимые прочностные характеристики материала диска. Коэффициент запаса прочности исследуемой конструкции по пределу текучести материала принять равным = 1,2.

При постановке первой задачи оптимизации установить (сформировать):

• вектор критериев эффективности;

• критерий оптимальности,

• вектор управляемых параметров;

• вектор неуправляемых параметров;

• функцию цели (целевую функцию);

• пространство проектирования,

• прямые ограничения,

• функциональные ограничения,

• область поиска оптимальных решений,

• область допустимых решений,

• число испытаний системы.

Решение первой задачи оптимизации выполнить следующими методами:

• методом дихотомического деления,

• методом золотого сечения,

• методом чисел Фибоначчи.

Сопоставить результаты решения данной задачи различными методами и дать оценку эффективности применяемых методов решения.

На втором этапе оптимального проектирования найти оптимальный профиль диска по критерию минимума материалоемкости изделия, обеспечив при этом работоспособность конструкции

При постановке второй задачи оптимизации установить (сформировать):

• вектор критериев эффективности;

• критерий оптимальности,

• вектор управляемых параметров;

• вектор неуправляемых параметров;

• функцию цели (целевую функцию);

• пространство проектирования,

• прямые ограничения,

• функциональные ограничения,

• область поиска оптимальных решений,

• область допустимых решений,

• число испытаний системы

Для решения второй оптимизационной задачи применить следующие методы:

• метод ненаправленного сканирования,

• метод статистических испытаний (метод Монте-Карло),

• метод направленного сканирования,

• метод поисковой оптимизации.

Сопоставить результаты решения задачи различными методами и дать оценку эффективности применяемых методов решения.

Для расчета напряженно-деформированного состояния исследуемых конструкций диска в процессе решения оптимизационных задач применить систему инженерного анализа «Disk2».

Исходные данные

Таблица 1

Вариант	T = T(r)
1

Таблица 2

№	a, мм	b, мм	c, мм	h =h (r), мм	, 1/с	p, МПа	t1	t2
8	70	400	80	95 - 0,1875r	500	200	0,9375	125

Содержание:

1. Постановка первой оптимизационной задачи

На первом этапе оптимального проектирования диска необходимо определить оптимальное значение натяга и необходимое значение предела текучести, удовлетворяющие условиям, сформулированным в задании.

Для решения первой задачи оптимизации устанавливаем следующие параметры:

• Вектор критериев эффективности:

Критерий эффективности – показатель, который позволяет количественно производить оценку эффективности проектных решений.

В нашем случае критерий эффективности: (X)= , где – радиальное напряжение в нулевой точке диска при r = a.

• Критерий оптимальности:

Критерий оптимальности - наилучший вариант среди некоторого множества критериев эффективности.

В нашей задаче критерий оптимальности будет равен .

• Вектор управляемых параметров:

Вектор управляемых (изменяемых в процессе оптимизации) параметров:

X = {δ}, где δ – натяг между валом и диском.

• Вектор неуправляемых параметров:

Вектор неуправляемых (неизменяемых в процессе оптимизации) параметров:

Y = {a,b,c,h(r),ρ,μ,E,α,T(r),p,ω, , σT}.

• Функция цели (целевая функция):

Функция цели является обобщенным критерием оптимальности для задачи многокритериальной оптимизации.

Целевая функция в нашей задаче: C(X) = .

• Пространство проектирования:

Область допустимых и недопустимых проектных решений, определяет пространство проектирования G.

Пространство проектирования в нашей задаче G = 0 < δ < ∞.

• Прямые ограничения:

Прямые ограничения для первой оптимизационной задачи: 0 < δ < 1 мм.

• Функциональные ограничения:

Функциональные ограничения для первой оптимизационной задачи:

• Область поиска оптимальных решений:

Областью поиска оптимальных решений служит подпространство пространства проектирования G, которое определяется множеством точек X, удовлетворяющих прямым ограничениям на управляемые параметры:.

Область поиска оптимальных решений П = { 0 < δ < 1 },

• Область допустимых решений:

Область допустимых решений D определяется множеством допустимых решений, удовлетворяющих всем принятым ограничениям (прямым и функциональным):

Область допустимых решений D = { δ : , 0 < δ < 1 }

• Число испытаний системы:

Для каждого метода будем устанавливать своё число испытаний системы, исходя из результатов расчёта. Поэтому число испытаний системы приведём в заключении для каждого метода отдельно.