Лекция 3.

1.2. Модели электровакуумных ламп и транзисторов

Основные типы моделей

Электронные элементы цепей (лампы, транзисторы и т. п.) могут быть представлены схемными моделями или схемами замещения, состоящими из пассивных двухполюсников (линейных и нелинейных) и зависимых источников (всех четырех типов). В соответствии с режимом электрической цепи и задачей исследования эти модели можно подразделить на четыре группы:

— низкочастотные линейные слабосигнальные модели для квазилинейного режима на низких частотах;

— нелинейные модели постоянного тока для статического режима и больших низкочастотных сигналов;

— высокочастотные линейные слабосигнальные модели для квазилинейного режима па высоких частотах;

— нелинейные универсальные модели для переходных режимов при больших сигналах.

Вопрос о применении той или иной модели решают, чтобы достигнуть наилучшего компромисса между двумя противоречивыми требованиями: достаточно высокой степени точности отображения реальных процессов и предельной простоты модели. Можно было бы снять этот вопрос, повсеместно используя универсальные модели, как это принято в некоторых разработанных программах анализа схем. Но при этом решение сравнительно простых задач неоправданно усложняется. Поэтому, по крайней мере на современном этапе, следует обеспечить возможность представления электронных элементов их моделями на любом уровне.

При разработке моделей электронных элементов обычно используют два подхода. Один из них основан на представлении электронного прибора в виде «черного ящика», благодаря чему отпадает необходимость рассматривать внутренние физические процессы. Соответствующие характеристики и параметры модели получают на основании измерения напряжений и токов на внешних зажимах (полюсах) компонента. При другом подходе информацию, необходимую для построения модели электронного прибора, извлекают, как раз рассматривая протекающие внутри него процессы. Например, параметры модели транзистора вычисляют на основании его структуры и свойств используемых полупроводниковых

материалов (геометрических размеров, поверхностной концентрации, глубины залегания переходов, времени и коэффициента диффузии, температуры и т. д.).

Низкочастотные линейные модели

Для составления низкочастотных линейных моделей обычно используют первый из рассмотренных подходов. Он проверен многолетней практикой расчета низкочастотных схем в квазилинейном режиме и нашел широкое применение.

Рассматривая транзистор как трехполюсный компонент (рис. 1.8,а), можно представить зависимости между переменными составляющими токов и напряжений на входе и выходе шестью вариантами уравнений, основные из которых в матричной форме имеют вид:

(1.19)

(1.20)

(1.21)

Системы параметров g, r и h, являющихся элементами матриц в соответствующих уравнениях, можно определить для каждого способа включения транзистора (рис. 1.8,б — г) на основании статических характеристик

Таблица 1.1

Взаимосвязь параметров транзисторов

Исходный параметр	Вычисляемая величина
	r	g	h	Определитель
r
g
h

или непосредственно измерить при помощи соответствующей аппаратуры. Зависимости между параметрами различных систем приведены в табл. 1.1. На рис. 1.9 изображены наиболее широко распространенные низко-

частотные линейные модели транзистора. Параметры модели определяют через какую-либо систему параметров транзисторов, найденных для соответствующей схемы включения. Например, для транзистора в схеме с общей базой:

Подобные таблицы для пересчета параметров транзистора и его моделей при различных способах включения приведены в работе [111].

Низкочастотные модели электровакуумных ламп в квазилинейном режиме без сеточных токов (рис. 110,а) описывают уравнением вида (1.19):

(1.22)

где S — крутизна анодно-сеточной характеристики лампы, G_i — ее внутренняя проводимость.

Часто используют другие параметры — внутреннее сопротивление R_i и статический коэффициент усиления μ, причем

(1.23)

Рассматривая транзисторы и триоды как трехполюсные компоненты, можно представить их параметры особенными матрицами проводимости или сопротивления в соответствии с (1.16) и (1.18). Вид этих матриц за-

висит от нумерации полюсов или сторон многополюсного компонента, а также от системы используемых параметров и схемы включения, при которой они определены [109]. Так, особенную (матрицу проводимости транзистора для обозначений полюсов, принятых на рис. 1.11,а, можно записать через g-параметры в виде

(1.24)

Матрицу сопротивления для принятых на рис. 1.11,б обозначений сторон транзистора проще всего представить через r-параметры:

(1.25)

Воспользовавшись зависимостями, приведенными в табл. 1.1, можно записать особенные матрицы транзистора и через другие системы его параметров.

Матрица проводимости триода в квазилинейном режиме без сеточных токов (рис. 112,а) в соответствии с (1.22) имеет вид

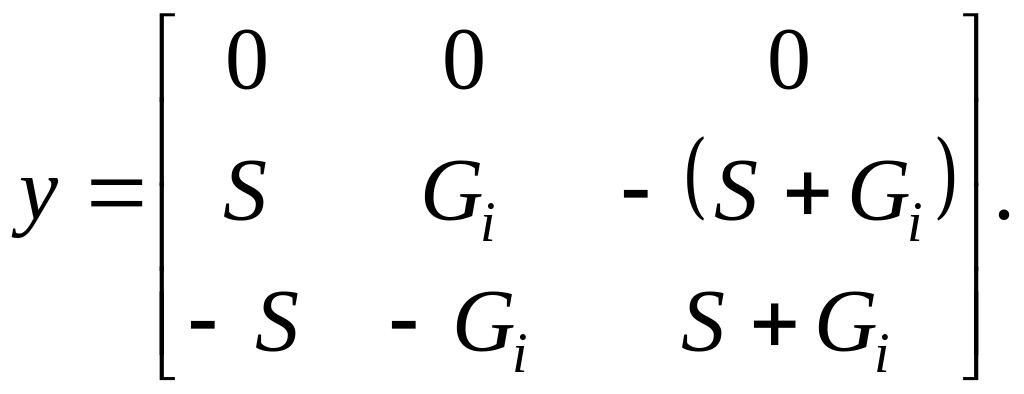(1.26)

Так как i_c=0, уравнение (1.22) нельзя разрешить относительно напряжений и матрица сопротивления идеального триода не существует. Однако, если рассматривать идеальный триод вместе с сеточным сопротивлением Z (рис. 1.12,б), то матрицу сопротивления запишем в виде.

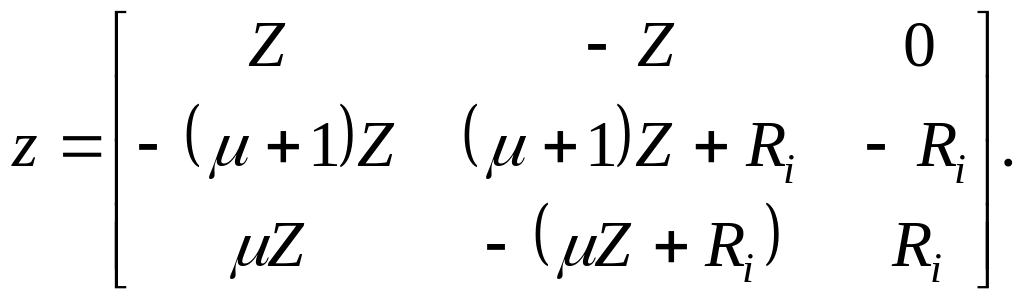(1.27)

Особенные матрицы многоэлектродных ламп получают аналогично, рассматривая их как многополюсные компоненты, причем порядок матриц равен числу электродов лампы, на которых напряжения и токи переменных составляющих отличны от нуля [109, 111].

Матричные параметры электровакуумных ламп и транзисторов являются их схемными моделями, характеризующими поведение этих компонентов в квазилинейном режиме. Экспериментальное определение параметров электронных компонентов на переменном токе в режимах холостого хода и короткого замыкания на их электродах [135] просто и удобно лишь на низких частотах, когда параметры выражаются вещественными числами. На высоких частотах параметры становятся комплексными и для их измерения требуется специальная прецизионная аппаратура.