Лекция 1 компоненты и топология схем

1.1. Компоненты электронных схем

Цепь и схема

Электромагнитные явления в электронных устройствах описываются сложными соотношениями и характеризуются величинами, зависящими как от времени, так и от пространственных координат. Однако такое описание является слишком общим и практически неприемлемым при исследовании и анализе сложных электронных устройств. Необходимых упрощений достигают, представляя электронные устройства как цепи с сосредоточенными элементами.

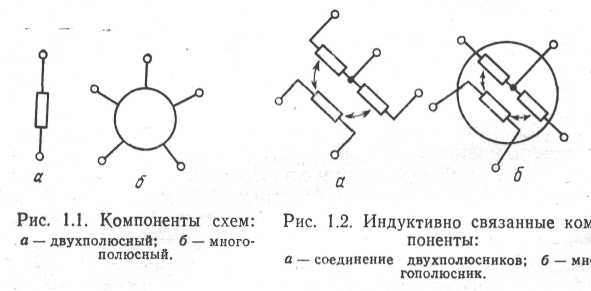
Электронная цепь характеризуется двумя основными показателями: набором элементов и способом их соединения. В зависимости от числа полюсов, различают двухполюсные и многополюсные элементы.

Свойства элементов описываются соотношениями между токами и напряжениями на их полюсах, заданными в аналитической, графической или табличной форме. Символы элементов представляют собой некоторые геометрические фигуры, а условные обозначения связей между ними обладают топологическими свойствами в том смысле, что любая их деформация на поверхности без разрывов не изменяет конфигурацию схемы. Вследствие этого одна и та же схема может быть изображена различными способами.

Простейшими элементами цепей являются резисторы, конденсаторы, катушки индуктивности, трансформаторы, электронные лампы, транзисторы, источники энергии и сигналов и другие элементы, входящие в состав электронных устройств. В виде элементов цепи могут быть представлены различные модули, твердотельные и интегральные цепи, а также монтажные и конструктивные элементы электронных устройств, существенно влияющие на характер электромагнитных процессов в этих устройствах.

При анализе электронных цепей реальные элементы представляют их схемными моделями (схемами замещения), вид которых зависит от режима работы элемента цепи, требуемой степени точности отображения протекающих в нем процессов, учета влияния внешних условий и т. п. Важнейшим следствием такого подхода является возможность свести огромное многообразие реальных элементов электронных цепей к сравнительно небольшому числу идеальных схемных компонентов, различные соединения которых отображают с необходимой степенью точности электронные цепи и их элементы. Таким образом, исследование электронных цепей заменяют по существу анализом соответствующих электронных схем.

Как и элементы цепи, схемные компоненты могут быть двухполюсными и многополюсными (рис. 1.1), причем многополюсные могут представлять собой объединение более простых компонентов. Связь между элементами может быть кондуктивной (гальванической, непосредственной), емкостной (электрической) и индуктивной (магнитной). Кондуктивную и емкостную связи отображают объединением соответствующих полюсов компонентов, а индуктивную — параметрами связи (взаимными индуктивностями),

Индуктивно связанные компоненты можно рассматривать и как двухполюсные с учетом взаимных связей (рис. 1.2,а), и как многополюсный, объединяющий группу индуктивно связанных компонентов (рис. 1.2,6).

Если токи и напряжения на компонентах схемы связаны линейными зависимостями, то такие компоненты называют линейными, а постоянные коэффициенты в этих зависимостях — их параметрами. Линейные компоненты, параметры которых являются функциями времени, получили отдельное название — параметрические. Компоненты, токи и напряжения которых связаны более общей зависимостью, отличающейся от линейной, называют нелинейными. Нелинейные компоненты могут быть также параметрическими. Соответственно схема является линейной, если все ее компоненты линейны, параметрической или нелинейной, если в нее входит хотя бы один параметрический или нелинейный элемент. Электронные цепи всегда нелинейны, но в ряде важных случаев они могут быть представлены линейными или параметрическими схемами, что заметно упрощает их анализ.

Двухполюсные компоненты

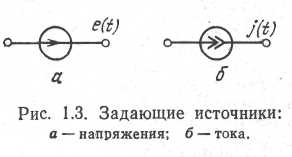
Источники энергии или сигналов отображают схемами, в которые входят идеальные источники напряжения или тока [24, 37]. Их условные обозначения показаны на рис. 1.3. Идеальный источник напряжения характеризуется задающим напряжением e(t), значение которого в любой момент времени не зависит от тока, протекающего через источник. Идеальный источник тока характеризуется задающим током j(t), значение которого в любой момент времени не зависит от напряжения на его полюсах. Реальные источники могут приближаться по своим свойствам к идеальным, но процессы в них всегда сопровождаются внутренними потерями энергии. Это учитывают в схемах введением пассивных элементов, которые представляют собой внутренние сопротивления источников.

Простейшие двухполюсные схемные компоненты представлены тремя типами: сопротивлениями, емкостями и индуктивностями.

В каждый момент времени токи и напряжения на двухполюснике характеризуются численным значением и направлением. Одно из двух возможных направлений принимают положительным и отмечают стрелкой. Условимся положительные направления тока и напряжения на двухполюснике выбирать взаимно противоположными.

Сопротивления определяются вольт-амперными характеристиками, представляющими зависимость между током и напряжением для каждого момента времени:

(1.1)

емкости — вольт-кулонными характеристиками, связывающими заряд и напряжение на этих компонентах:

(1.2)

а индуктивность — ампер-вебернымп характеристиками, представляющими зависимость между магнитным потоком и током компонента:

(1.3)

Ф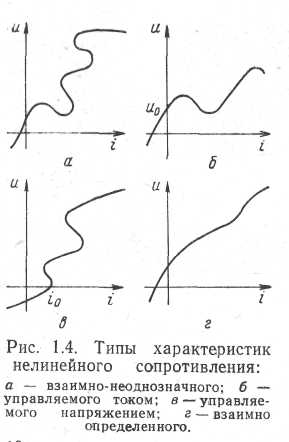 ункции (1.1) — (1.3) могут иметь различный характер. В качестве примера на рис. 1.4 приведены возможные вольт-амперные характеристики сопротивления. Одна из них (рис. 1.4,а) не определена однозначно относительно токов и напряжений и в дальнейшем из анализа исключается, две другие (рис. 1.4,б и в) могут рассматриваться в качестве однозначных явных функций только относительно изменений тока и напряжений соответственно (в связи с чем вводятся понятия о сопротивлениях, управляемых током или напряжением [52, 194]), и, наконец, четвертая (рис. 1.4,г) является взаимно определенной относительно изменений тока или напряжения.

По аналогии с характером кривых (рис. 1.4,б и в) для случая вольт-кулонных характеристик различают емкости, управляемые зарядом (током) или напряжением, а для случая ампер-веберных характеристик — индуктивности, управляемые потоком (напряжением) и током.

Статические параметры двухполюсных компонентов (статические сопротивления, емкости, индуктивности) определяются через координаты точек приведенные функций (1.1 - 1.3), а дифференциальные параметры (дифференциальные сопротивления, емкости, индуктивности) через наклоны этих функций. В достаточно малой окрестности некоторой точки характеристики дифференциальные параметры можно считать постоянными величинами, т. е. для малых изменений токов (зарядов) и напряжений (потоков) относительно этой точки нелинейный двухполюсник ведет себя как линейный.

Вольт-амперные характеристики некоторых схемных компонентов могут не проходить через начало координат. Тогда при I = 0 напряжение u₀ на сопротивлении отлично от пуля (рис. 1.4,б) или при u = 0 через него протекает ток i₀ (рис. 1.4,в). Компоненты, токи и напряжения которых отличны от нуля в режиме короткого замыкания или холостого хода относительно их полюсов, получили название автономных двухполюсников и многополюсников [37].

Зависимые источники

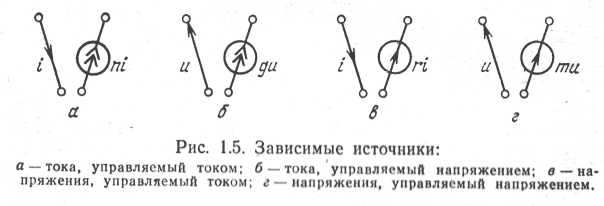
Схемными компонентами являются также зависимые источники тока и напряжения [104], отображающие необратимость электронных схемных компонентов: источники тока, управляемые током (рис. 1.5,а) и напряжением (рис. 1.5,б), а также источники напряжения, управляемые током (рис. 1.5,в) и напряжением (рис. 1.5,г). Зависимые источники являются многополюсными компонентами, включающими собственно источник и управляющий двухполюсник. Роль последнего может играть любой двухполюсный компонент схемы, ток или напряжение которого управляет током или напряжением зависимого источника. Величины п, g, r, m (рис. 1.5) являются управляющими параметрами зависимых источников.

В общем случае зависимым источником может управлять напряжение между любой парой узлов схемы, причем управляющим двухполюсником служит включенная между этими узлами разомкнутая ветвь, сопротивление которой R=∞. Аналогично управляющим по току двухполюсником может служить короткозамкнутая ветвь, сопротивление которой R = 0. Часто удобно рассматривать собственно зависимые источники и управляющие двухполюсники как отдельные компоненты схемы.

Эквивалентные операторные схемы

Линейные двухполюсные компоненты при нулевых начальных условиях можно представить уравнениями в операторной форме:

(1.4)

(1.5)

в которых операторные сопротивления Z(p) для омического сопротивления, емкости и индуктивности записываются как

(1.6)

а операторные проводимости Y(p) соответствующих компонентов как

(1.7)

где D и Г — параметры, обратные емкости и индуктивности соответственно.

Важнейшее значение операторного представления уравнений линейных компонентов заключается в том, что интегро-дифференциальные соотношения во временной области преобразуются в алгебраические в комплексной области. Операторные изображения токов и напряжений I(p) и U(р) характеризуют состояние компонента (или схемы). Перейти к соответствующим им функциям времени можно на основе аппарата обратного преобразования [111].

Комплексную переменную p = a+jw можно рассматривать как некоторый оператор. Иногда ее называют комплексной частотой. Это связано с тем, что при гармонических воздействиях р = jw, где w — частота гармонических колебаний. Однако понятие комплексной частоты гораздо шире обычно применяемого к гармоническим функциям и сигналам, и его используют для описания непериодических функций времени.

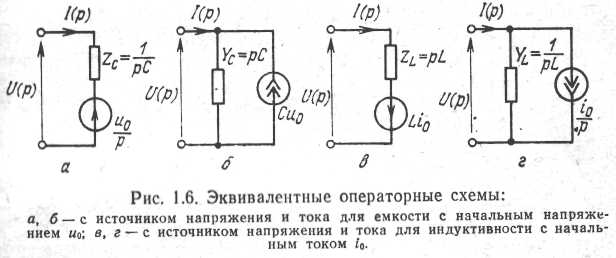
Выражения (1.6) и (17) формально можно распространить и на нелинейные компоненты, если под р понимать оператор дифференцирования d/dt, а под R, С и L — соответственно дифференциальные сопротивление, емкость и индуктивность.

При отличных от нуля начальном напряжении и₀ на емкости и токе i₀ в индуктивности можно воспользоваться эквивалентными операторными схемами, представленными на рис. 1.6 [111].