22. Интервальная оценка ожидаемого значения зависимой переменной в парной регрессионной модели.
Определим доверительный интервал для ожидаемого значения зависимой переменной:
,
Составляется дробь Стьюдента
нормированная ошибка оценки (прогноза) среднего значения эндогенной переменной, где в числителе — истинная ошибка оценки (прогноза), в знаменателе — оценка ско данной ошибки
По
точечной оценке
формируется
интервальная оценка, с границами
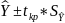
23. Интервальная оценка индивидуального значения зависимой переменной в парной регрессионной модели.
Границы доверительного интервала прогноза индивидуальных значений :
Функция Стьюдраспобр при уровне значисоти α=0,05 и число степеней свободы равно ячейке V2
24. Алгоритм проверки адекватности парной регрессионной модели.
1) деление выборки на две части: обучающую (90-95% наблюдений) и контролирующую (5-10% наблюдение)
2) Настройка модели по обучающей выборке (оценка параметров МНК)
3) Построение прогноза эндогенной переменной из контролирующей выборки
Ŷp = â + b̂Xp
Построение интервальной оценки эндогенной переменной из контролирующей выборки
Y –p = Ŷp - tкр*Sp Y +p = Ŷp + tкр*Sp
4) Выполнение проверки
Y –p < Yp < Y +p : да – > модель адекватна, нет – > модель не адекватна
25. Коэффициент детерминации регрессионной модели.
Коэффициент детерминации в парной регрессионной модели
Коэффициент детерминации показывает долю дисперсии результативного признака x, объясняемую регрессией, в общей дисперсии y. Иными словами, долю влияния фактора на изменение результативного показателя.
Например, коэффициент детерминации равен 0,78. Это значит, что изменения результативного показателя на 78% объясняются изменениями уравнения регрессии или модель среднего качества.
Представим выборочное значение дисперсии зависимой переменной в следующем виде:
или для вариации
В выражении (1) предполагается, что
Часто уравнение (1) записывают в следующих обозначениях:
где
– необъясненная
регрессией (остаточная) сумма квадратов
отклонений (error sum
of squares);
=
‑ объясненная регрессией сумма
квадратов отклонений (regression
sum of squares);
=
‑ общая сумма квадратов отклонений
зависимой переменной от ее среднего
выборочного значения (total
sum of squares).
Качество подгонки регрессионной модели к наблюденным значениям
,
оценивается при помощи статистики
—коэффициента детерминации.
Коэффициентом детерминации называется статистика, определяемая по формуле (справедливо только в случае выполнения (2)):
Из формулы (3) следуют два масштабирующих значения для коэффициента детерминации:
•
,
при
в этом случае регрессор
не
улучшает качество оценки (прогноза)
,
по сравнению с тривиальной оценкой
(прогнозом)
;
•
,
при
,
в этом случае все точки наблюдения лежат
на регрессионной прямой (т. е.
,
или
).
Таким образом, чем
ближе значение коэффициента детерминации
к 1, тем лучше качество подгонки
(аппроксимация облака наблюдений
линейной функцией) и оценка
более точно аппроксимирует наблюдения
.
Если (2) не выполняется, то коэффициент детерминации не обязан принимать значения от нуля до единицы.
Выражение (3) можно проинтерпретировать следующим образом:
т. е. коэффициент детерминации — это доля дисперсии зависимой переменной, объясненная уравнением регрессии.
Очевидно, чем лучше регрессия аппроксимирует результаты наблюдений, тем больше должен быть коэффициент корреляции между фактическими (наблюдаемыми) и оценочными значениями зависимой переменной (и наоборот).
Коэффициент детерминации во множественной регрессионной модели
Для определения качества подгонки множественной регрессионной модели к наблюдаемым значениям , используется коэффициент детерминации :
где
—
n-мерный вектор-столбец
центрированных (по выборочному среднему)
значений зависимой переменной
В множественной регрессионной модели добавление дополнительных регрессоров, как правило, увеличивает значение коэффициента детерминации (4), поэтому его корректируют с учетом числа регрессоров
здесь в числителе дроби несмещенная оценка дисперсии возмущений, в знаменателе — несмещенная оценка дисперсии эндогенной переменной .