73. Оценка моделей с распределенными лагами с бесконечным числом лагов: метод геометрической прогрессии.

Спецификация модели:

Yt= α+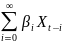 +εt

Предпосылки относительно параметров:

β_i=β₀λⁱ, i=0,1,2,… 0<λ<1

λ – характеристика скорости убывания коэффициентов с увеличением лага

Модель с геометрически распределенными лагами:

Спецификация модели:

Yt= α+β₀X_t+β₀λX_t-1 + β₀λ²X_t-2 +… +ε_t

α, β_0,λ – неизвестные параметры

Оценка неизвестных параметров осуществляется по данному алгоритму:

1. параметр λ принимает значения из интервала (0,1) с некоторым шагом (например, 0,01; 0,001; 0,0001)

2. Для каждого значения λ рассчитывается значение переменной

Z_t(P) = X_t + λX_t-1 + λ²X_t-2 + λ³X_t-3 +… +λ^p X_t-p

Значение максимального лага p подбирается из условия:

<δ,

То есть при дальнейшем добавлении лаговых значений переменной Х величина изменения Z_t будет меньше любого ранее заданного числа δ

3. Оценивается спецификация вида

Yt= α+β₀Z_t(P)+εt

Из всех возможных значений λ выбирается то значение, при котром коэффициент детерминации R² для этой модели будет наибольшим.

4. Найденные параметры α, β_0,λ используются в спецификации модели с геометрически распределенными лагами.

74. Оценка моделей с распределенными лагами с бесконечным числом лагов: метод Койка.

Алгоритм преобразования:

Yt=α+β₀X_t+β₀λX_t-1 + β₀λ²X_t-2 +… +ε_t

• результат первого шага

λY_t-1=λα+β₀X_t+β₀λX_t-1 + β₀λ²X_t-2 + β₀λ³X_t-3 +… +λε_t-1

• результат второго шага

Yt - λY_t-1=(1-λ)α+β₀X_t+ (εt -λε_t-1)

Результат преобразования:

Спецификация авторегрессионной модели

Yt=(1-λ)α+β₀X_t+ λY_t-1+ν_t, где

ν_t= ε_t- λε_t-1 – скользящая средняя между ε_t,ε_t-1.

Таким образом, при помощи преобразования Койка

1. модель с бесконечным числом лагов (с убывающими по степенному закону параметрами) сводится к авторегрессионной модели, для котрой требуется оценить только три параметра α, β_0,λ.

2. Устраняется мультиколлинеарность, часто возникающая при оценке параметров с лаговыми переменными.

75. Проблемы оценки параметров регрессионных моделей с распределёнными лагами методом Койка

Спецификация авторегрессионной модели после преобразования Койка:

.

При применении преобразования Койка возможны следующие проблемы:

1. Спецификация включает стохастический регрессор, коррелирующий со случайным возмущением. Т.е. среди регрессоров появляется лаговая переменная , которая представляет собой стохастический регрессор, что нарушает одну из предпосылок Гаусса-Маркова для классической регрессионной модели, данная случайная переменная коррелирует со случайным возмущением.

2. Случайные возмущения исходной модели с распределенными лагами не коррелированы, случайные возмущения авторегрессионной модели автокоррелированы. Для случайных возмущений исходной модели справедлива предпосылка о некоррелированности, а для случайного возмущения преобразованной модели имеет место автокорреляция.

При указанных выше проблемах оценки, полученные по МНК, являются смещёнными и несостоятельными.

76. Оценка моделей с распределенными лагами: метод Алмон.

Распределенные лаги Алмон имеют большую гибкость по сравнению с преобразованными лагами методом Койка. Преимуществом данного метода распределения является возможность моделирования больших случаев, чем это позволяет преобразование Койка (к примеру, когда изменение зависимой переменной в ответ на изменение регрессоров сначала невелико, затем со временем возрастает, затем снова убывает).

В основе модели лежит предположение о том, что если Y зависит от текущих и лаговых значений Х, то веса в этой зависимости подчиняются полиномиальному распределению, т.е.:

Поэтому лаги Алмон назывваются также полиномиально распределенные лаги. Для простоты рассмотрения метода выберем степень полинома равной двум, тогда:

(1)

Подставив в спецификацию регрессионной модели с распределенными лагами данное преобразование, получим:

Далее следует ввести следующие обозначения:

1. 

2. 

3. 

С учетом данных преобразований модель примет вид:

Значения параметров определяются по МНК. При этом случайные возмущения удовлетворяют условиям Гаусса – Маркова. Параметры β определяются из соотношения(1).

Для применения схемы Алмон необходимо определить количество лагов k. Обычно его определяют подбором, начиная с «разумного» максимального, постепенно его уменьшая. Затем подбирается степень полинома m. При этом используется правило: степень полинома должна быть по крайней мере на единицу больше количества точек «экстремума» (точек, разделяющих интервалы возрастания и убывания) в зависимости . С ростом полинома повышается риск наличия неучтенной мультиколлинеарности в силу спецификации построения . Это увеличивает стандартные ошибки параметров .