57. Примеры спецификаций регрессионных моделей нелинейных по параметрам.
Среди нелинейных функций, которые могут быть приведены к линейному виду, в эконометрических исследованиях очень широко используется степенная функция (5).
(5)
Данное соотношение легко преобразовать в линейное уравнение с помощью логарифмирования (5):
(6)
После введения новых переменных, обозначающих логарифмы, получается линейное уравнение (6). Тогда процедура оценивания регрессии состоит в вычислении новых переменных для каждого наблюдения путём взятия логарифмов от исходных значений.
(7)
Затем оценивается регрессионная зависимость новых переменных. Для перехода к исходным переменным следует проэкспонировать полученные показатели. Аналогично можно рассматривать случай показательных или экспоненциальных функций.
показательная ; (8)
экспоненциальная . (9)
Пример: производственная модель Кобба-Дугласа.
Спецификация модели:
Прологарифмируем модель:
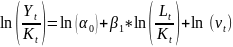
Замена переменных:
Спецификация линеаризованной модели:
Оценённая модель Кобба-Дугласа:
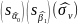
Вычисление оценок параметров:
.
58. Интерпретация параметров регрессионных моделей нелинейных по параметрам.
- значение эндогенной переменной при единичном значении регрессора.
Параметр
называется коэффициентом регрессии.
Его величина показывает среднее изменение
результата с изменением фактора на одну
единицу.
Параметр в степенной функции имеет четкое экономическое истолкование, т. е. он является коэффициентом эластичности. Это значит, что величина коэффициента показывает, насколько процентов изменится в среднем результат, если фактор изменится на 1%.
59. Способы включения случайных возмущений в спецификацию нелинейной по параметрам модели.
1. Мультипликативное включение:
Исходная спецификация:
Линеаризованная спецификация:
Замена переменных:
Распределение
вектора возмущений
-
нормальное с параметрами:
логнормальное
распределение с параметрами:
Исходная спецификация:
Линеаризованная спецификация:
Распределение
вектора возмущений
-
нормальное с параметрами:
2. Аддитивное включение:
Исходная спецификация:
Логарифмическое преобразование:
Вывод:
Логарифмическое преобразование не приводит к линеаризации модели.
60. Спецификация и оценивание мнк эконометрических моделей нелинейных по переменным.
Более простым является класс нелинейных переменных, в которых имеется нелинейность, но которые остаются линейными по входящим в них и подлежащих оценке параметрам. Сюда входят полиномы различной степени и равносторонняя гипербола. Такая нелинейная регрессия по включённым переменным в объяснение переменных простым их преобразованием (заменой) легко сводится к обычной линейной регрессии для новых переменных. Поэтому оценка параметров в этом случае выполняется просто по МНК, поскольку зависимости линейны по параметрам.
Так, важную роль в экономике играет нелинейная зависимость, описанная равносторонней гиперболой (1):
.
(1)
Произведём замену
переменных: обозначим
.
В результате получается линейная модель:
(2)
Её параметры хорошо оцениваются по МНК, и сама зависимость характеризует связь удельных расходов сырья, топлива, материалов с объёмом выпускаемой продукции, временем обращения товаров и всех этих факторов с величиной товарооборота.
В общем случае парабола второй степени, так же как и полиномы более высокого порядка, при линеаризации принимают вид уравнения множественной регрессии:
парабола второй
степени
.
(3)
Применим метод
замены переменных:
После преобразования получается линейная
модель:
(4)
Следовательно, полином любого порядка сводится к линейной регрессии с ее методами оценивания параметров и проверки гипотез. Как показывает опыт большинства исследователей, среди нелинейной полиномиальной регрессии чаще всего используется парабола второй степени; в отдельных случаях – полином третьего порядка. Ограничения в использовании полиномов более высоких степеней связаны с требованием однородности исследуемой совокупности: чем выше порядок полинома, тем больше изгибов имеет кривая и соответственно менее однородна совокупность по результативному признаку.