7.3. Электрөткізгіштіктің температураға тәуелділігі.

Электрөткізгіштіктің температураға тәуелділігін анықтау үшін, электрондардың тор тербелістерінен, қоспа атомдардан шашырауын еске алу керек. Тордың тербелістерін дыбыс кванттары фонондармен сипаттайды. Металдың электрөткізгіштігін (кедергісін) жоғарыда айтылған процестерді кванттық тұрғыдан қарастыру арқылы тапса, төмендегі түрде жазуға болады

(7.3.1)

мұндағы - химиялық потенциалдармен (Ферми деңгейімен 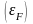) анықталатын шекті жылдамдық - электронның фонондар, электрондар және қоспа атомдармен әсерлесуін (шашырауын) сипаттайтын еркін жүру жолының ұзындықтары. Электронның фонондармен әсерлесуін қарастырған кезде, фонондар жиілігінің жоғары жағынан ( -дыбыс жылдамдығы, а-тор тұрақтысы) жиілікпен шектелгендігін еске алу керек. Осы жиілікке сәйкес келетін температура дебай температурасы деп аталады.

Егер металдың температурасы болса, есептеулер екенін көрсетеді, олай болса меншікті кедергі температураға тура про­порционал болады. Ал болса,

(7.3.2)

төменгі температураларда меншікті кедергі температура төмендеген сайын оның бесіншi дәрежесіне пропорционал кемиді. Электрондардың өзара кулондық әсерлесуін сипаттайтын . Сонымен катар электрондар, фонондар алмасу аркылы да өзара әсерлесетінін еске алса

(7.3.3)

Көптеген металдар үшін болғандықтан . Электрондардың қоспа атомдардан шашырауының кедергіге қосатын үлесін анықтайтын температураға байланысты емес, қоспа атомдардың концентрациясымен анықталады. Шынында ( - қоспа атомдардың бірлік көлеміндегі саны, - электрондардың қоспа атомдардан шашырауының эффектілік қимасы). Сондықтан

Егер , екенін еске алсақ,

Қатты денелердің зоналық теориясы туралы мағлұматтар. Металл құрамына кіретін еркін электрондарды да сипаттайтын физикалық шамалар дискретті мәндер қабылдайды. Қатты денелерде электрондардың мүмкін энергетикалық деңгейлері бipiгіп зоналар құрайды. Зоналардың құрылуын түсіну үшін жеке атомдардың катты дене құрамына кірместен бұрын дискретті энергетикалық деңгейлерінің құрылысын қарастыралық (7.4.1-сурет). Осы атомдар бip-бipiнe жақындап қатты дене түзеген кезде атомдардың электрондық қабыршактарындағы электрондар әсерлесіп олар белгілі-бір энергетикалық деңгейлерге орналаса бастайды. Бұл кезде фермиондардың (электрондардың) Паули принципіне бағынатыны ерекше роль атқарады. Паули принципі бойынша фермионның күйін анықтайтын төрт кванттың сандары (n-бас, L-орбиталдық, m-магниттік, m - спиндік кванттык сандар), бірдей екі фермион бip энергетикалық деңгейде орналаса алмайды. Бip энергетикалық деңгейде орналаскан екі фермионның ең болмағанда бip кванттық саны бірдей болмауы керек. Мысалы, бip энергетикалық деңгейде орналасқан екі электронның спиндері бірдей болмауы, яғни олар қарама-қарсы жаққа бағытталуы керек, ceбeбi спиндік моменттің белгілі бip бағытта проекциясы екі ғана мән кабылдайды ( ].

7.4.1-сурет

Сондықтан катты дене кристалының түйіндерінде орналасқан атомдар (иондар) құрамына кіретін электрондар және бip-бipiнe өте жакындаған (кристалл тұрақтысына тең аралыкка) кезде электрондық қабыршактардан бөлініп шыккан еркін электрондар (металдардағы) екі-екіден (спиндері карама-карсы) энергетикалық деңгейлерде орналасады. Осы кезде барлық атомдардың Е, деңгейлері бірігіп бip зона, Е деңгейлері бірігіп екінші зона т.с.с зоналар түзіледі. Kөршi зоналардың арасындағы энергетикалық деңгейлерде электрондар бола алмайды. Бұл аралықтарды жабық зоналар деп атайды (7.4.2-сурет). Катты денелердің көпшілік электрлік, магниттік және оптикалық қасиеттері жоғарғы зоналарда орналасқан (Е = О деңгейге жақын орналасқан) электрондармен (валенттік және еркін (өткізгіштік)) анықталатын болғандықтан, ең жоғарғы үш зонаны қарастырады. Олар: валенттік зона (в.з.), жабық зона (ж.з.) және өткізгіштік зона (ө.з.). Осы үш зонаның құрылысына қарай қатты денелерді үш класқа бөледі: металдар, шала өткізгіштер және диэлектриктер. Металдарда жабық зонаның ені өте аз бip зонаға кіретін деңгейлердің аралығындай болатындықтан, өткізгіштік зонамен валенттік зона бip-бipiмeн жалғасып жатады, валенттік зона толық толтырылмаған болады.

7.4.2- сурет

Жартылай өткізгіштерде жабық, зонаның ені бірнеше электронвольттан аспайды, валенттік зона толық толтырылған болады, ал диэлектриктерде жабык зонаның eні жүздеген және одан да үлкен электронвольтка жетеді, валенттік зона толык толтырылған болады (7.4.3-сурет).

7.4.3-сурет

Металдарда валенттік және өткізгіштік зоналар жалғасып жататындыктан, аз электр өрісінің әсерінен электрондар бағытталган қозғалысқа келіп, өткізгіш арқылы ток жүреді. Шала өткізгіштерде өткізгіштік зонаға электрондар өтуі үшін жабық зонаның енінен кем емес энергия әсер етуі керек. Егер онша үлкен болмаса, жылулык энергия электронды өткізгіштік зонаға көшіруге жеткілікті болады, яғни шала өткізгіш арқылы жүру мүмкіндігі туады. Диэлектриктерде жылулық қозғалыс энергиясы елерліктей электрондар санын өткізгіштік зонаға көшіре алмайды, сондыктан өpic тесіп өту (пробой) мәніне жеткенше диэлектрик аркылы ток жүре алмайды.

7.5. Ферми-Дирак таралуы және металдардың классикалық теориясының кейбір қиыншылықтарының шешілуі. Металдағы еркін электрондардың энергия бойынша қалай таралғанын анықтау үшін, электрондарды олармен араластырылған статистикалық тепе-тендік күйдегі молекулалармен соктығысады деп қарастыралық. Мұндай молекулалар Максвелл таралуына бағынуы керек, яғни . Энергиясы 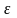электрон энергиясы молекуламен соктығыскан кезде олардың энергиялары , болу ьқтималдығы болса, осы процесс кезінде электрондардың бірлік уакыт ішінде өзгеру саны

(7.5.1)

Бұл кезде энергияның сакталу заңы орындалуы тиіс. Егер электрондардың Паули принципіне бағынатындығын еске алсақ, электрон энергиясы 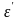күйге өту үшін, бұл күй бос болуы керек, яғни (7.5.1) көбейтілуі керек

(7.5.2)

қЕнді энергиясы күйге келетін электрондар саны

(7.5.3)

Уақытты керіге өзгерткенде механикалық заңдардың өзгермейтінін еске алсақ . Электрондардың молекулалармен соктығысуы нәтижесінде бірлік уақытта өзгеруі

(7.5.4)

Статистикалық тепе-тендік күйде соңғы теңдік нөлге тең болуы керек, яғни

(7.5.5)

Соңғы теңдікке Максвелл таралуын койсақ,

(7.5.6)

Энергиянын сақталу заңы бойынша , олай болса

(7.5.7)

(7.5.7) теңдіктің бip жағы -ге, екінші жағы тәуелді, бipaқ, өзара тең болғандықтан, теңдіктің екі жағы да бip тұрақтыға тең болуы керек. Егер тұрактыны түрінде алсак,

(7.5.8)

Бұдан

(7.5.9)

О сы формула электрондық газдың статистикалық тепе-теңдік күйде энергия бойынша таралуын анықтайды. Таралу функциясының энергияға тәуелділігі 7.5.1-суретте көрсетілгендей болады. Егер және 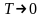болғанда =1, ал болса болады, яғни баспалдакты түрде өзгереді.

7.5.1-сурет Бұлай болатын ceбeбi температура абсолюттік нөлге тең болған кезде -ге сәйкес келетін энергияға дейін деңгейлер түгел электрон­дармен толтырылған, ал одан энергиясы үлкен деңгейлер бос болды. Осы денгейді Ферми деңгейі деп атайды. Температура нөлден өзге және kT « болғанда таралу функциясы маңында ғана елерліктей өзгереді.

Енді көлемдегі энергиялары және аралығында болатын электрондардың санын табу үшін координаталар мен импульс компоненттерінен тұратын фазалық кеңістікті қарастырамыз. Бұл кеңістіктің элементіндегі күйлердің санын табу үшін оны бөлу керек.

Координаталар кеңістігіне байланыссыз, импульстің шамасы мен аралығында жататын фазалық кеңістіктегі күйлер саны

(7.5.10)

Импульстің орнына энергияны айнымалы шама деп есептесек,

,

(7.5.11)

Бip күйде спиндері қарама-қарсы екі электрон болу мүмкіндігін ескерсек, энергиялары және аралығында жататын электрондар саны

Электрондардың толық саны

(7.5.12)

Соңғы формула электрондардың концентрациясын тұрақты шама -мен байланыстырады.

Егер болса, (7.5.12) өрнектегі интегралдың шектеpi 0 және болуы керек, яғни

(7.5.13)

Олай болса

,

Электрондық газдың туындау температурасы деп аталады. Электрондық газдың кездегі толық энергиясы

(7.5.14)

Энергияның температураға тәуелділігін анықтау үшін (7.5.14) интегралды жуықтап есептеуге болады. Ол үшін Ферми-Дирак таралуын шекаралық энергиялары және болатын екі баспалдақты функциялардың жарты қосындысына тең деп есептеуге болады

(7.5.15)

мұндағы 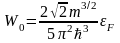абсолюттік нөлдегі электрондық газдың энергиясы. Ферми деңгейі (энергиясы) үшін (7.5.13) формуланы пайдалансақ,

(7.5.16)

Электрондық газдың жылу сыйымдылығы

Бip электронның үлесіне келетін жылу сыйымдылық

(7.5.17)

Сонымен электрондык газдың жылу сыйымдылығы температураға тура пропорционал екен. Металдардағы еркін электрондарды Максвелл таралуына бағынатын болса, екенін білеміз. Осы екі жылу сыйымдылықтардың қатынасы

(7.5.18)

яғни электрондык газдың металдың жылу сыйымдылығына қосатын үлесі аз болуы керек