2. Векторная диаграмма

Это совокупность векторов на комплексной плоскости ,отображающих синусоидально изменяющиеся функции времени одинаковой частоты и по­строенных с соблюдением их взаимной ориентации по фазе.

Они позволяют производить сложение и вычитание синусоидальных функций времени.

Пример:

Дано: (2.75)

Найти:

Г еометрическая сумма векторов и дает комплексную ампли­туду искомого тока. Длина вектора равна амплитуде тока, а угол между дей­ствительной осью и самим вектором равен начальной фазе искомого тока.

Рис.40

Указанное свойство позволяет осуществить наглядную интерпретацию закона Кирхгофа на комплексной плоскости. Кроме того векторные диа­граммы дают нам реальное представление о фазовых отклонениях между на­пряжением и током идеальных элементов (участков цепи).

1). . (2.76)

Рис.41

2). . (2.77)

Рис.42

3). . (2.78)

Рис.43

Частным случаем векторной диаграммы является топографическая век­торная диаграмма, на которой вектора рисуются последовательно, друг за другом, а порядок их расположения соответствует порядку расположения элементов цепи.

3. Комплексная форма записи мощности

(2.79)

Перейдём к комплексным действующим значениям:

. (2.80)

Рис.44

Введём в рассмотрение сопряжённый комплекс тока . (2.81)

(2.82)

где – комплексная мощность.

9. Методы расчёта линейных электрических цепей

Задачей расчёта является: определение токов в ветвях, потенциалов в отдельных точках цепи или напряжения между отдельными точками.

При этом должны быть известны конфигурация цепи и параметры её отдельных элементов.

Методы, изложенные ниже, приводятся для цепи синусоидального тока, они же справедливы и для цепей постоянного тока, который следует рассматривать как частный случай переменного с частотой равной нулю.

1. Метод преобразования

Используется, когда цепь имеет один источник электрической энергии.

Состоит в приведении сложной разветвлённой цепи путём преобразо­ваний к простейшей, содержащей одно сопротивление.

Правила преобразований:

1. Замена последовательно включённых элементов одним эквивалент­ным.

Э лементы включены последовательно, если по ним течёт один и тот же ток.

Рис.45

(2.81)

2. Замена параллельно включённых элементов одним эквивалентным.

С опротивления включены параллельно, если они имеют общую пару узлов.

Рис.46

. (2.82)

Частный случай: для двух параллельно включенных проводников

. (2.83)

3. Преобразование «звезда» - «треугольник»

Рис.47

– треугольник в звезду. (2.84)

– звезда в треугольник. (2.85)

П ример:

Рис.48 Рис.49

. (2.86)

Рис.51 Рис.50

(2.87)

. (2.88)

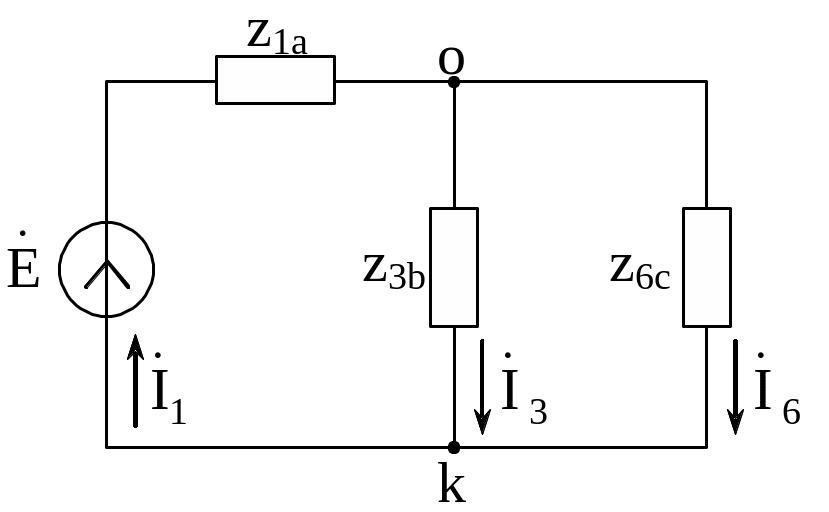
Рис.52 Рис.53

. (2.89)

Находя токи, возвращаемся по схемам обратно.

; (2.90)

; (2.91)

; (2.92)

; (2.93)

; (2.94)

; (2.95)

; (2.96)

. (2.97)

2. Расчёт цепей с помощью законов Кирхгофа

Пусть схема содержит n ветвей с источником ЭДС и источниками тока.

Причём m – число источников тока, отсюда число неизвестных токов (n-m).

Метод законов Кирхгофа сводится к составлению и решению системы из (n-m) уравнений относительно неизвестных токов.

Пусть k – число узлов в цепи, из принципа непрерывности тока следует, что число линейно независимых уравнений, которые можно составить по первому закону Кирхгофа, равно (k-1).

Недостающие уравнения составляем по второму закону Кирхгофа для независимых контуров.

Число уравнений по второму закону Кирхгофа равно n-m-(k-1).

Контуры следует выбирать так, чтобы они не содержали источник тока, поскольку напряжение на зажимах источника тока заранее не известно.

,

,

Рис.54

(2.98)

Недостаток рассмотренного метода – его громоздкость, так как для схемы с большим числом ветвей получим систему с таким же количеством уравнений.

3. Метод контурных токов

Пусть схема не содержит источников тока. Расчёт цепи может быть сведён к решению всего n-(k-1) уравнений, составленных по второму закону Кирхгофа.

Для этого цепь мысленно рассматривают как совокупность независи­мых соприкасающихся контуров, по которым текут контурные токи.

Направления контурных токов выбирают произвольно, а обход конту­ров совершают в направлении контурных токов. Затем по особым правилам для выбора контуров составляют уравнения (по второму закону Кирхгофа).

Рис.55

Рис.56

Эти уравнения имеют вид:

(2.99)

(2.100)

Пусть цепь содержит р - независимых контуров , тогда система уравне­ний будет содержать уравнения типа:

. (2.101)

. (2.102)

– контурные токи.

– контурное сопротивление р-го контура (сумма сопротивлений ветвей, образующих р-й контур)

– сопротивление связи, сопротивление ветви, общей для р-го и q-го контуров.

Если в общих (смежных), ветвях направления контурных токов совпадают, то сопротивление связи берётся со знаком +, иначе –.

Поскольку , то полученные матрицы обладают симметрией относительно главной диагонали.

– контурная ЭДС р-го контура (алгебраическая сумма ЭДС входящих в р-й контур).

Если направление контурного тока совпадает с направлением ЭДС, то она берётся со знаком +, иначе –.

Для схемы 1:

(2.103)

Для схемы 2:

(2.104)

После определения контурных токов рассчитывают фактические токи в ветвях. Токи в ветвях принадлежат только одному контуру, равны соответственно контурным токам или могут отличаться по направлению.

Для схемы 1:

Для схемы 2:

Токи в ветвях общих для двух или нескольких контуров равны сумме соответствующих контурных токов.

Для схемы 1: .

Для схемы 2:

Если схема содержит источника тока, то выбирается контур, содержащий этот источник тока. Уравнение для него не составляется, так как контурный ток равен, току самого источника.

П адения напряжения на сопротивлениях связи от источника тока переносится в правую часть оставшихся уравнений.

Рис.56

4. Метод узловых потенциалов

Если в электрической цепи число узлов без единицы меньше числа независимых контуров, то удобно воспользоваться методом узловых потенциалов. Он сводится к составлению и решению системы из (к-1) уравнений относительно неизвестных потенциалов узлов (узловых потенциалов).

При этом потенциал одного из узлов полагают равным нулю. Эти уравнения вытекают из первого закона Кирхгофа, и составляются по определённым правилам.

Так для любой цепи с тремя узлами система в общем случае имеет вид:

(2.105)

Для цепи с четырьмя узлами:

(2.106)

В общем случае система любого порядка содержит уравнения типа:

, (2.107)

.

Здесь: – потенциалы соответствующих узлов.

– сумма проводимостей ветвей сходящихся в n-ом узле.

– проводимость ветвей соединяющих узел n с узлом q.

– узловой ток n-го узла.

– ЭДС в ветвях между узлами n и q.

Если источник ЭДС направлен к узлу n, то он берётся с плюсом, иначе с минусом.

Аналогично для токов источников между узлами n и q.

Составим систему (2.108) для схемы 1:

Составим систему (2.109) для схемы 2:

После решения системы и определения потенциалов узлов находим токи в ветвях с помощью закона Ома.

Для схемы 1:

; ;

; .

5. Замена нескольких параллельных ветвей, содержащих источник ЭДС и тока одной эквивалентной

Условия эквивалентности:

При любой величине тока , напряжения у обеих схем должны быть одинаковы.

. (2.110)

(2.111)

Тогда:

. (2.112)

Пусть цепь содержит n параллельных ветвей тогда:

. (2.113)

Для эквивалентной схемы:

. (2.114)

Сравнивая (2.113) и (2.114) видим:

.

. (2.115)

. (2.116)

Если направление эквивалентной ЭДС и какого-либо источника ЭДС в цепи совпадают, то последнее берётся с плюсом, иначе с минусом.

Аналогично действуют для источников тока.

6. Принцип наложения и метод наложения

Принцип наложения: ток в любой ветви равен алгебраической сумме токов, вызываемых каждым источником электрической энергии цепи в отдельности.

Принцип суперпозиции справедлив для любой линии электрической цепи. Используется в методе расчёта, называется методом наложения.

Порядок расчёта:

Поочерёдно рассчитывают токи, возникающие от действия каждого источника в отдельности, мысленно удаляя остальные источники в цепи, но оставляя в ней внутреннее сопротивление источников. Это значит, что участок цепи, в которой был ЭДС, закорачивается, а с источником тока разрывается. Затем находят фактические токи в ветвях, путём суммирования частичных токов.

; ; ; .

Рис.58

7. Метод эквивалентного генератора

Используется для определения тока в одной ветви электрической цепи.

В ывод: выделим из электрической цепи ветвь с искомым током, а остальную часть мысленно заключим в прямоугольник.

Рис.59

Если последовательно с нагрузкой включить две одинаковые, и направленные друг к другу ЭДС, то искомый ток не изменится. .

Пусть исходная цепь содержит n источников электрической энергии, тогда согласно принципу наложения искомый ток равен.

. (2.117)

Под током будем понимать ток, вызванный всеми источниками исходной цепи и ЭДС .

Ток вызывается только источником , и в прямоугольнике отсутствуют источники электрической энергии.

. (2.118)

. (2.119)

Подберём такую, чтобы .

Последнее эквивалентно размыканию ветви с искомым током (режиму холостого хода).

. (2.120)

Тогда:

, (2.121)

где – комплексное входное сопротивление пассивного двухполюсника, со стороны зажимов ab.

Рис.60

Перепишем (2.121) в виде

. (2.122)

Уравнению (2.122) соответствует схема:

Рис.61

Часть схемы заключённую в пунктир можно рассматривать как эквивалентный генератор, ЭДС которого , а внутреннее сопротивление .

Порядок исполнения метода эквивалентного генератора.

В соответствии с направлением искомого тока производим разметку зажимов нагрузки и указываем стрелкой направление .

Удаляем сопротивление нагрузки и рассчитываем в полученной цепи напряжение .

Находим входное сопротивление пассивного двухполюсника со стороны зажимов ab.

Пользуемся формулой (2.122).

П ример:

Рис.62

. (2.123)

. (2.124)

. (2.125)

. (2.126)

Опытное определение параметров эквивалентного генератора:

Измеряем величину .

Измеряем ток короткого замыкания.

. (2.127)