1. Математический анализ

1. Числовая последовательность и ее пределы

Определение 1.1.1. Если каждому значению n из натурального ряда чисел 1, 2, …n ставится в соответствии по определенному закону некоторое вещественное число x_n, то множество занумерованных вещественных чисел будет называться числовой последовательностью x_п.

Примеры:

1. n²=1, 2², 3²….,n²…

2. 1+(-1)ⁿ=0, 2, 0, 2,…

3.  =

Определение 1.1.2. Последовательность x_п называется ограниченной сверху (снизу), если существует вещественное число M (соответственно m), такое что для всех элементов x_n выполняется неравенство:

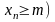(соответственно (1.1.1)

При этом, число M (m) называется верхней гранью (нижней гранью), а неравенство ( условием ограниченности.

Определение 1.1.3. Последовательность x_п называется ограниченной, если она ограничена и сверху и снизу, то есть если существуют вещественные числа m и М, такие что для всех элементов x_n выполняется условие:

(1.1.2)

Примеры:

1. Последовательность 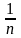 = является ограниченной, так как любой ее элемент удовлетворяет условию (2) при любых

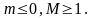
2. Последовательность n²=1, 2², 3²….,n²… ограничена снизу m=1 и неограниченна сверху.

Рассмотрим последовательность чисел:

х₁, х₂, х₃,…., х_n……

Определение 1.1.4. Число a называется пределом последовательности х_п, если для любого    найдется такой номер , что при n   выполняется неравенство

х_n  a    (1.1.3)

Последовательность, имеющая предел, называется сходящейся и записывается это следующим образом:

Пример 1. Доказать по определению предела последовательности чисел, что .

Возьмем любое число

Посмотрим, при каких номерах (п) будет выполняться неравенство

(*) ,

где  - любое положительное число?

Упростим выражение, стоящее под модулем

, получим .

Учитывая, что под модулем стоит отрицательное число, получим 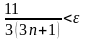, следовательно , и окончательно

(**) .

Если выполняется неравенство (**), то выполняется и неравенство (*). Найдем номер N(?

Очевидно, что если , то и неравенства (**) и (*) выполняются для всех п = 1,2,3,…, то есть N ( = 0.

Если , то 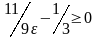, и за номер N( можно взять целую часть  , то есть N ( =  .

Основные свойства сходящихся последовательностей:

1. Сходящаяся последовательность имеет только один предел.

2. Сходящаяся последовательность ограничена.

3. Сумма (разность) сходящихся последовательностей х_п и у_п есть сходящаяся последовательность, предел которой равен сумме (разности) пределов последовательностей х_п и у_п.

4. Произведение сходящихся последовательностей х_п и у_п есть сходящаяся последовательность, предел которой равен произведению пределов последовательностей х_п и у_п.

5. Частное двух сходящихся последовательностей х_п и у_п при условии, что предел последовательности у_п отличен от нуля, есть сходящаяся последовательность, предел которой равен частному пределов последовательностей х_п и у_п.

Вычисление пределов числовых последовательностей часто требует умения раскрывать неопределенности вида ^_. Если общий член последовательности представляет собой дробь с многочленами в числителе и знаменателе, надо разделить числитель и знаменатель дроби на п^к - старшую степень знаменателя, и использовать свойства пределов.

Пример 2.

Для ряда примеров на раскрытие неопределенности типа ^_ необходима техника работы с дробными показателями.

Пример 3.

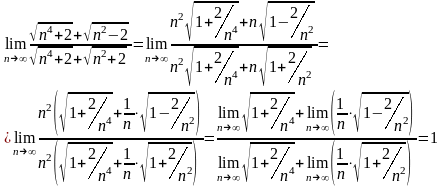
Чтобы раскрыть неопределенность типа «    », в ряде случаев рекомендуется выражение под знаком предела умножить и соответственно разделить на сопряженное ему выражение. Примеры сопряженных выражений:

Пример 4.