1

Общее уравнение прямой

Общее уравнение прямой линии на плоскости в декартовых координатах:

где  ,   и   — произвольные постоянные, причем постоянные   и   не равны нулю одновременно. Вектор с координатами   называется нормальным вектором, он перпендикулярен прямой. Вектор с координатами (−B, A) или (B, −A) называется направляющим вектором.

При   прямая проходит через начало координат. Также уравнение можно переписать в виде

Свойства прямой

Через любые две несовпадающие точки можно провести единственную прямую.

• Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или являются параллельными.

• В трёхмерном пространстве существуют три варианта взаимного расположения двух прямых:

  • прямые пересекаются;

  • прямые параллельны;

  • прямые скрещиваются.

• Прямая линия — алгебраическая линия первого порядка: в декартовой системе координат прямая линия задается на плоскости уравнением первой степени (линейное уравнение).

2

Уравнение окружности радиуса  R  с центром в точке О ( х₀ ,  у ₀ ) имеет вид:

 

( х – х₀ ) ²  + ( у – у ₀ ) ² = R ² .

 

Если центр окружности совпадает с началом координат, то уравнение окружности упрощается:

 

х ²  +  у  ² = R ² .

 

Пусть  Р ( х₁ ,  у ₁ ) – точка окружности ( рис.1 ), тогда  уравнение касательной к окружности в данной точке имеет вид:

 

( х₁ – х₀ ) ( х – х₀ )  + ( у₁ – у ₀ ) ( у – у ₀ ) = R ² .

 

Условие касания прямой  y = m x + k  и окружности  х ²  +  у  ² = R ² :

 

 

k 2  / ( 1 + m ² ) = R ² .

 

3

	Прямая линия - график линейной функции y = ax + b. Функция y монотонно возрастает при a > 0 и убывает при a < 0. При b = 0 прямая линия проходит через начало координат т. 0 (y = ax - прямая пропорциональность)
	Парабола - график функции квадратного трёхчлена у = ах2 + bх + с. Имеет вертикальную ось симметрии. Если а > 0, имеет минимум, если а < 0 - максимум. Точки пересечения (если они есть) с осью абсцисс - корни соответствующего квадратного уравнения ax2 + bx +с =0
	Гипербола - график функции  . При а > О расположена в I и III четвертях, при а < 0 - во II и IV. Асимптоты - оси координат. Ось симметрии - прямая у = х(а > 0) или у - - х(а < 0).
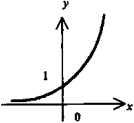
	Экспонента (показательная функция по основанию е) у = еx. (Другое написание у = ехр(х)). Асимптота - ось абсцисс.
	Логарифмическая функция y = logax (a > 0)
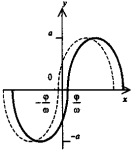
	у = sinx. Синусоида - периодическая функция с периодом Т = 2π
	у = а•sin(ωx+φ) - функция гармонических колебаний. Обозначения: а - амплитуда, ω - частота (ω = 2π/Т), φ - фаза (сдвиг).
	Косинусоида у = cosx (графики у = sinx и у = cosx сдвинуты по оси х на  )
	Тангенсоида y = tgx. Точки разрыва при х =  (2k -1), где k = 0, ±1, ±2,.. Вертикальные асимптоты в этих точках.
	Гауссиана у = Аe-(ax2). Кривая "нормального" закона распределения ошибок, у которого ,  , σ 2 - дисперсия ошибки. Симметрия относительно оси у.
	у = secx - кривая "цепной линии", эту форму принимает абсолютно гибкая нить, подвешенная в параллельном поле тяжести. А полная функция периодична, и её асимптоты х =  (2k -1), как у функции y = tgx.
	Круг с центром в точке (xo, yo) радиуса r. (x-xo)2 + (y-yo)2 = r2
	Эллипсс центром в точке (xo, yo). Большая полуось а, малая b, эксцинтриситет ,
	Затухающее колебание y = Ae-ax•sin(ωx+φ)

7

Комплексное число. Действительная часть. Мнимая часть

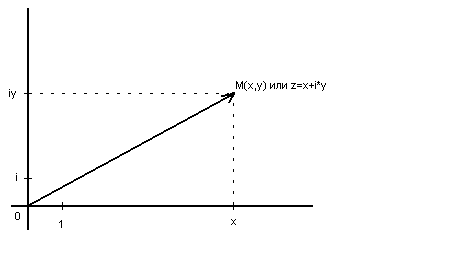
     Определение 1: Комплексным числом z называется пара действительных чисел (x,y), такая что z = x + i*y.  x является действительной частью комплексного числа z и обозначается x = Re(z), а y - мнимая часть комплексного числа z и обозначается y = Im(z), i -  мнимая единица :  i*i = - 1, т.е. мнимая единица в квадрате равна минус единице.

     Рассмотрим геометрическую интерпретацию комплексных чисел. В декартовой системе координат на оси ординат будем отмечать значения мнимых частей комплексных чисел и ось назовем мнимой осью, а на оси абсцисс будем отмечать действительные части комплексных чисел и назовем эту ось действительной осью. Тогда любая точка М(x,y) может быть представима на плоскости следующим образом:

Комплексные числа

    Если соединить начало координат с точкой M некоторым вектором, то координаты вектора будут в точности совпадать с координатами точки М. Вообще говоря, между векторами выходящими из начала координат и комплексными числами взаимнооднозначное соответствие, т.е. каждому комплексному числу соответствует только один вектор и каждому вектору соответствует только одно комплексное число.

8

Та запись комплексного числа, которую мы использовали до сих пор, называется алгебраической формой записи комплексного числа. Часто бывает удобна немного другая форма записи комплексного числа. Пусть   и φ = arg z. Тогда по определению аргумента имеем: 

Отсюда получается 

z = a + bi = r(cos φ + i sin φ).

Такая форма называется тригонометрической формой записи комплексного числа. Как видно, для того, чтобы перейти от алгебраической формы записи комплексного числа к тригонометрической форме, нужно найти его модуль и один из аргументов.

9