Електричні коливання

Вільні незгасаючі електричні коливання виникають у коливальному електричному контурі, зображеному на рисунку нижче. Контур складається з конденсатора ємністю С і котушки індуктивністю L.

Якщо зарядити конденсатор до значення заряду , а потім замкнути коло коливального контуру перемикачем, то конденсатор почне розряджатися. У колі з'явиться електричний струм і в котушці індуктивності виникне ЕРС самоіндукції Енергія електричного поля конденсатора буде переходити в енергію магнітного поля котушки, і навпаки.

Будуть таким чином відбуватися незгасаючі коливання заряду, якщо енергія контура не розсіюватиметься.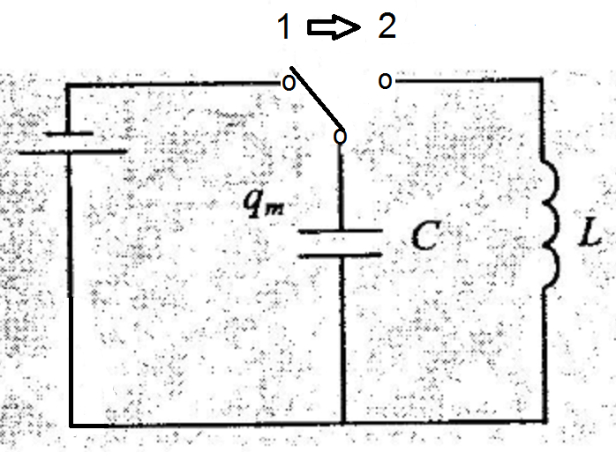

Щоб дістати диференціальне рівняння електричних коливань, скористаємось узагальненим законом Ома для неоднорідно кола:

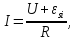
звідки

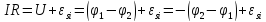= 0.

Тут враховано, що активний опір кола R = 0.

Різниця потенціалів на обкладках конденсатора

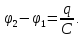
ЕРС самоіндукції

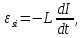
а сила струму

I =

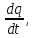
і тоді

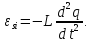
Підставивши вирази для різниці потенціалів і ЕРС у закон Ома, дістанемо

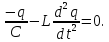
Поділивши рівняння на L і ввівши позначення

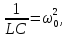
дістанемо ДИФЕРЕНЦІАЛЬНЕ РІВНЯННЯ ВІЛЬНИХ НЕЗГАСАЮЧИХ ЕЛЕКТРИЧНИХ КОЛИВАНЬ

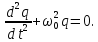
За формою рівняння цілком ідентичне рівнянню вільних незгасаючих механічних коливань:

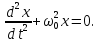
Видно, що заряд q - аналог зміщення x; індуктивність L - аналог маси m; 1/C - аналог жорсткості k.

Розв'язок диференціального рівняння також має аналогічний вигляд:

q = q_m cos(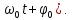

Період коливань визначиться з умови:

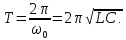
ШВИДКІСТЬ ЗМІНИ ЗАРЯДУ, яка дорівнює першій похідній від заряду за часом, це СИЛА СТРУМУ:

I =

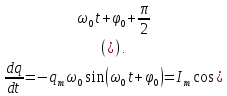
Сила струму в коливальному контурі виконує гармонічні коливання, частота яких дорівнює власній частоті контура 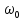, амплітуда сили струму залежить не тільки від амплітуди коливань заряду, а й від частоти, а фаза коливань струму відрізняється від фази коливань заряду на .

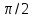ЕНЕРГІЯ ЕЛЕКТРИЧНОГО ПОЛЯ - це енергія зарядженого конденсатора

ЕНЕРГІЯ МАГНІТНОГО ПОЛЯ - це енергія, нагромаджена в котушці:

Оскільки L і С пов'язані через власну частоту:

то:

L =;

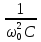а формулу для енергії магнітного поля можна записати так:

=.

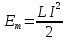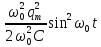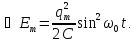
Отже, амплітуди коливань електричної і магнітної енергії однакові, а частота коливань вдвічі більша від частоти коливань заряду і струму.

ПОВНА ЕНЕРГІЯ електромагнітних коливань дорівнює сумі електричної і магнітної енергії

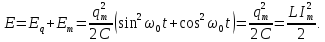
Як бачимо, повна енергія не залежить від часу, вона стала. Повна енергія дорівнює максимальному значенню енергії магнітного поля в котушці, або максимальному значенню енергії електричного поля в конденсаторі.

Фізичний і математичний маятники

Фізичним маятником називають будь-яке тіло, підвішене не за центр тяжіння (точка С). При відхиленні від вертикалі на кут α виникає момент сили тяжіння

,

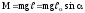який приводить тіло в обертальний рух відносно точки підвісу О. Запишемо основне рівняння динаміки обертального руху

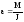, або .

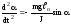Знак (–) враховує, те що момент сили зменшує кут відхилення, тобто напрям відхилення, наприклад, вправо, протилежний дії моменту сили тяжіння, вліво (див. рисунок).

При малих кутах відхилення, коли 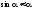, рівняння набуває виду

.

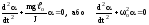Тут 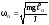- циклічна частота коливань фізичного маятника. Тоді період коливань визначається формулою:

.

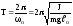Математичний маятник – це матеріальна точка, підвішена на невагомій нерозтяжній нитці. Його можна розглядати як різновидність фізичного маятника з моментом інерції матеріальної точки . Тоді період коливань математичного маятника буде визначатися по формулі

.

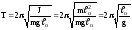Якщо у формулі періоду коливань фізичного маятника позначити 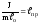, вона набуде виду, аналогічного періоду коливань математичного маятника. Зведеною довжиною фізичного маятника називається така довжина математичного маятника, період коливань якого дорівнює періоду коливань фізичного маятника.

Отже, фізичний і математичний маятники здійснюють гармонічні коливання при малих кутах відхилення .
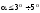