§ 1. Диференціал довжини дуги.

§ 2. Кривизна кривої. Коло кривизни. Еволюта. Евольвента.

§ 1. Диференціал довжини дуги.

Нехай криву задано параметрично:

x = x(t), y = y(t), α ≤ t ≤ β,

де x(t), y(t) – неперервні на y(t) відрізку [α;β] функції разом з похідними x'(t), y'(t).

Візьмемо на кривій (рис.1.) точку М, яка відповідає довільно вибраному значенню параметра t. Тоді крива А˘М є спрямлюваною, а довжина дуги

Оскільки верхня межа в цьому інтегралі є змінною, то

Рис. 1. інтеграл є функцією верхньої межі t. Отже, і s є функцією від t:

s = s(t).

Знайдемо похідну функції s(t). Похідна цієї функції в точці t існує і дорівнює

.

Звідси

.

Записуючи x'(t), y'(t) у вигляді

х' = , у' = ,

дістаємо таку формулу для диференціала дуги А˘М:

,

або

ds² = dx² + dy².

Користуючись останньою формулою можна надати геометричну інтерпретацію.

Справді, нехай криву задано рівнянням у = f(х), де f(х) неперервна на відрізку [a;b] разом з похідною f '(х) функція. Тоді крива А˘М є спрямлюваною.(рис.2.)

Візьмемо на цій кривій дві довільні точки М(х; у) і М'(х + ∆х; у + ∆у). Позначимо довжину дуги ММ' через ∆ ѕ і в точці М проведемо дотичну.

Тоді d ѕ дорівнює довжині гіпотенузи прямокутного трикутника з катетами dх і dу. У цьому й полягає геометричний зміст диференціала дуги

З формули можна дістати формули для диференціала дуги в різних системах координат, зокрема:

Рис. 2.

1) в декартовій системі координат крива задається рівнянням у = f(х), тоді

dх; (1)

2) крива задана параметричними рівняннями:

х = х(t), у = у(t),

тоді

(2)

3) в полярних координатах крива задана рівнянням ρ = ρ(φ),

тоді

(3)

Остільки ѕ(t) є монотонно зростаючою функцією, (ѕ'(t) > 0), то для функції ѕ = ѕ(t) (t) існує обернена функція t = ω(ѕ). Тому, підставляючи в рівняння кривої

х = х(t), у = у(t) значення t, дістанемо такі рівняння:

х = х(ω(ѕ)) = φ(ѕ),

у = у(ω(ѕ)) = ψ(ѕ),

0 ≤ ѕ ≤ S.

Це параметричні рівняння кривої, де за параметр взято вже довжину дуги – геометричну величину, яка пов’язана з кривою.

§ 2. Кривизна кривої. Коло кривизни. Еволюта. Евольвента.

Будь – яка крива в різних точках має не однаковий ступінь викривлення. Так. парабола у = х² поблизу початку координат викривлена більше, ніж в точках, які знаходяться далі від початку координат. Коло в усіх своїх точках має однакове викривлення.

Різні криві також відрізняються одна від одної своїм ступенем викривлення. Пряма лінія викривлень не має. Коло малого радіуса викривлено більше, ніж коло великого радіуса.

Виникає запитання: що ж прийняти за міру кривизни кривої в окремих точках? Щоб відповісти на це питання, припустимо,що до кривої в кожній точці можна про вести дотичну і що крива є спрямлюваною.

Візьмемо на кривій дві точки М і М' (рис. 3) і в цих точках проведемо дотичні прямі. Нехай дотична МΝ утворює з додатнім напрямом осі Ох кут α , а пряма М'Ν' - кут α + ∆α.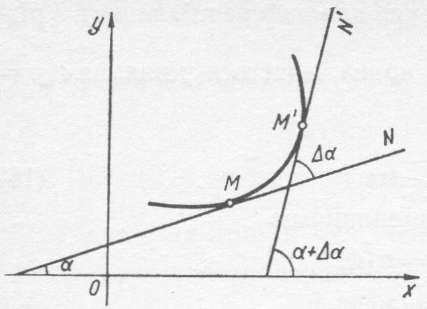

Довжину дуги ММ' позначимо через ∆ѕ.

Означення 1. Модуль відношення │ │, де ∆α – величина кута в радіанах, на який повертається

Рис. 3 дотична,коли точка М переміститься вздовж кривої

в точку М', називається середньою кривизною дуги ММ'

Означення 2. Границю, якщо вона існує,середньої кривизни дуги ММ', коли точка М' наближається вздовж кривої до точки М, називають кривизною кривої в точці М і позначають

К = │ │ (4)

Приклади.

1). Знайти кривизну кола радіуса R в довільній точці.

Розв’язання.

Візьмемо на колі дві довільні точки М і М' і проведемо в них дотичні до кола. Довжина дуги ММ' кола ∆s = R ∆α. Тому середня кривизна

│ │ = є сталою. Тоді і │ │ = . Отже, кривизна кола в кожній точці стала: К = . Звідси випливає, що чим менший радіус кола, тим більша кривизна, і навпаки, чим більший радіус кола, тим менша його кривизна.

2). Знайти кривизну прямої лінії.

Розв’язання.

У цьому разі дотична в кожній точці збігається із заданою прямою. Тому кут її повороту ∆α = 0.Середня кривизна │ │ = 0, а отже, і │ │ = 0. Таким чином, кривизна прямої в кожній її точці дорівнює нулю.

Виведемо тепер формули для обчислення кривизни кривих, заданих в різних системах координат. Нехай криву задано в декартовій системі координат рівнянням у = f(х), де функція f(х) на відрізку [a;b] має похідні до другого порядку включно.

Скористаємося формулою(4). Очевидно, що коли М'→М, то довжина дуги ∆s → 0. Тому формулу (4) можна записати ще так:

К = │ │ (5)

Крім того, позначивши через α кут, утворений дотичною до кривої у точці М( х; f(х)) з додатнім напрямом осі Ох, дістанемо

tg α = f '(х).

Звідси

α = arctg f '(х),

dα = dх

Підставляючи у формулу (5) значення dα і значення ds із формули(1), дістаємо формулу для кривизни кривої

К = (6)

З цієї формули легко дістати формулу для кривизни кривої, коли остання задана параметричними рівняннями х = х(t), у = у(t). Справді, якщо функції х = х(t), у = у(t) мають на відрізку [α; β] похідні до другого порядку включно і х'(t) ≠ 0, то

у_х' = ,

Тоді, підставляючи значення у формулу (6) відповідно замість f ''(х), f '(х),дістанемо формулу

К = (7)

Якщо криву задано в полярній системі координат рівнянням ρ = ρ(φ), α ≤ φ ≤ β, то поклавши φ = t, матимемо параметричні рівняння кривої

х = ρ(φ) соs φ, у = ρ(φ) sіn .φ

Знаходячи відповідні похідні і підставляючи їх у формулу (7), матимемо формулу для кривизни кривої:

К = (8

Означення3. Величину, обернену до кривизни кривої в даній точці, називають радіусом кривизни кривої і позначають

R = .

Означення 4. Коло, радіус якого дорівнює радіусу кривизни в даній точці, називають колом кривизни.

Приклади.

1. Обчислити кривизну параболи у = х² в точці (1; 1).

Розв’язання. Застосуємо формулу (6). Для цього знайдемо f '(х) = 2х,

f ''(х) = 2, f '(1) = 2, f ''(1) = 2.

Тоді

К = =

2) Знайти кривизну кардіоїди ρ = a(1 – cоs φ) в довільній точці.

К = .