Зразки розв’язування задач

1. Знайти довжину кола.

Розв’язання

Візьмемо коло радіуса з центром в початку координат. Його рівняння .

Щоб використати формулу (27.7) знайдемо . Знак плюс відповідає верхній половині кола, знак мінус – нижній.

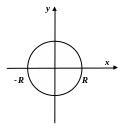
Знайдемо довжину чверті кола, що лежить в першій координатній чверті. Обчислимо вираз .

Маємо: , , 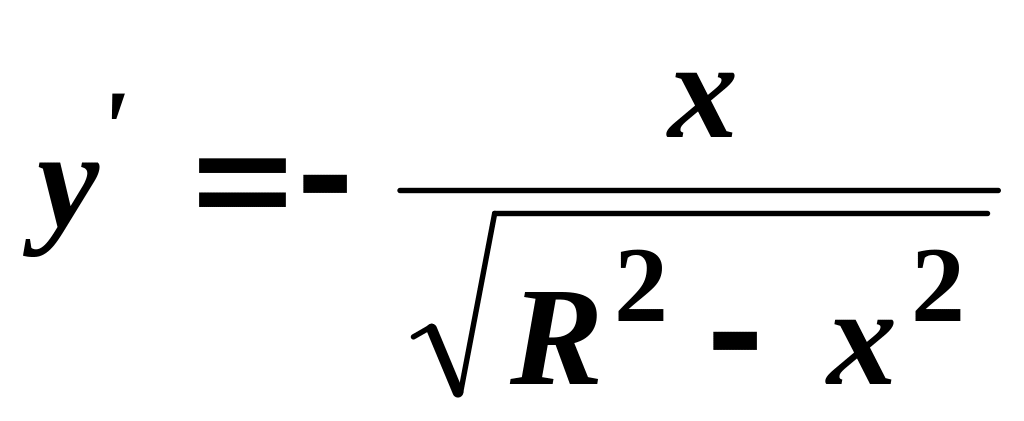тоді , тобто .

Абсциса точки кола в першій чверті змінюється від до . Тоді . Довжина кола .

Розв’яжемо цю ж задачу, якщо коло задано параметричними рівняннями:

.

Щоб застосувати формулу (3.9) обчислимо .

.

На всьому колі параметр змінюється від до . Тому

.

Ще більш простим буде розв’язування цієї задачі, якщо рівняння кола задати у полярних координатах. Покладемо , . Рівняння кола: , , тобто , звідки .

Полярна вісь співпадає з додатнім напрямком осі , а полярний кут , коли точка пробігає все коло, змінюється від до . За формулою (3.10):

2. Знайти довжину ланцюгової лінії між точками з абсцисами і .

Розв’язання

Знайдемо , тоді

.

Обчислимо: . За формулою (27.7): .

3. Знайти довжину дуги лінії від точки до .

Розв’язання

Застосуємо формулу (27.8):

, тоді

.

Отже,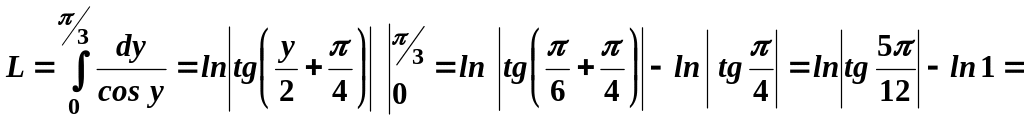

.

(Модуль знято тому, що - кут першої чверті і ).

4. Обчислити довжину дуги кривої від точки до ( ).

Розв’язання

Застосуємо формулу (27.7): , .

Тоді .

Отримаємо: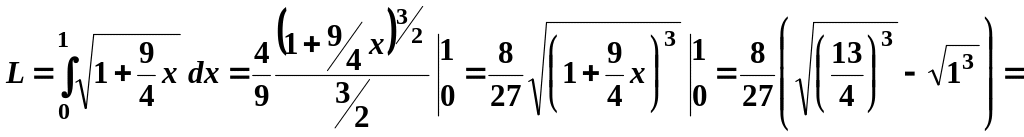

.

5. Знайти довжину астроїди .

Розв’язання

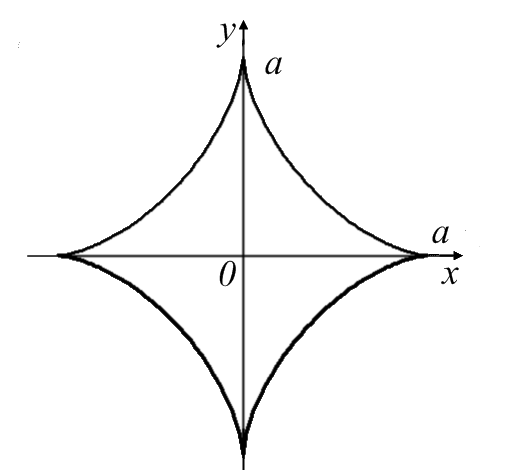Наведемо вигляд цієї кривої.

Користуючись симетрією, обчислимо довжину дуги, що розташована у першій чверті. Вона становитиме чверть від всієї довжини дуги.

З рівняння дістанемо: .

Піднесемо обидві частини рівності до степеня . Отримаємо: .

Тоді .

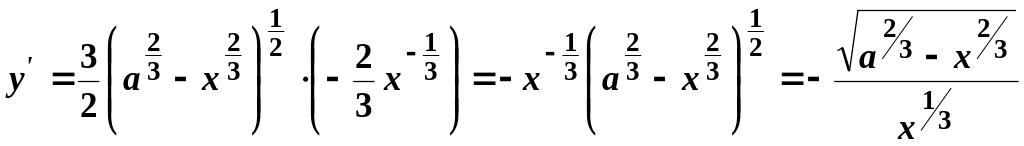Обчислимо .

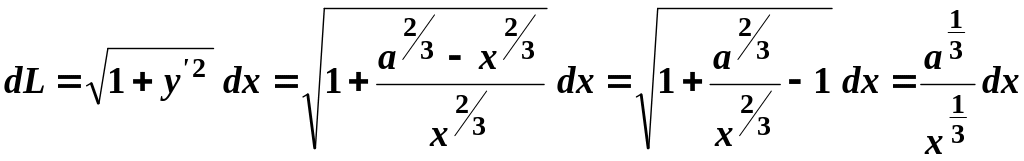Маємо: .

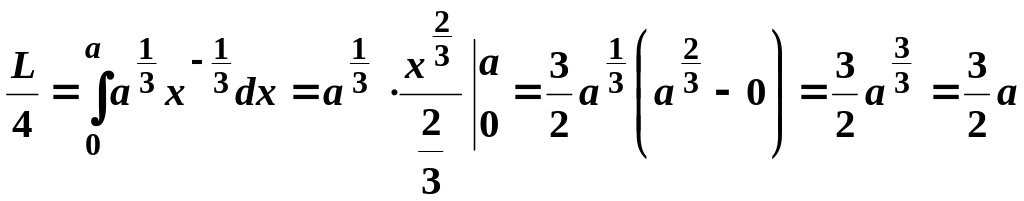Тоді .

6. Знайти довжину однієї арки циклоїди .

Розв’язання

Згадаємо приклад 9 попереднього параграфа: параметр кривої змінюється від до .

Застосуємо формулу (27.9): , .

Обчислимо

.

Тоді .

Тобто довжина однієї арки циклоїди у вісім разів більша радіуса кола, яке її утворює.

7. Знайти довжину дуги кривої , від до .

Розв’язання

Знайдемо : ,

.

Тоді

Тоді .

8. Визначити довжину всієї кривої Штейнера .

Розв’язання

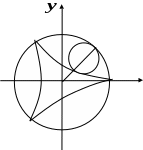Якщо , рухоме коло описує третину всієї кривої. Знайдемо :

,

.

Будемо мати:

.

Маємо: . Отже, .

9. Знайти довжину кардіоїди .

Розв’язання

Н

аведемо вигляд цієї кривої.

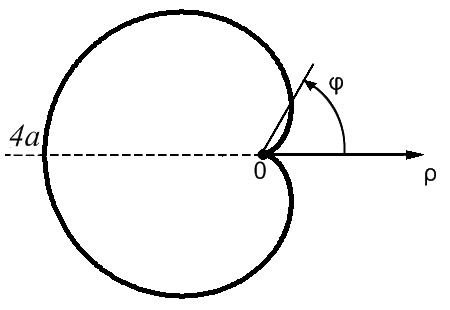
Для використання формули (27.10) обчислимо та . Маємо: , ,

тоді

.

У той час, коли точка на кардіоїді пробігає всю криву, її полярний кут змінюється від до .

.

10. Знайти довжину дуги кривої .

Р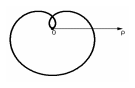 озв’язання

Довжину дуги обчислимо за формулою (3.10). Для цього знайдемо диференціал дуги .

Маємо:

.

Тоді

.

Визначимо, як змінюється полярний кут, коли точка, що рухається по кривій, пробігає її всю. Нехай , тоді , звідки . При , при .

Отже,

.

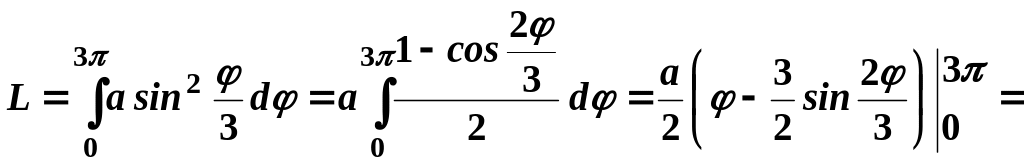
Знайти довжину дуги першого витка спіралі Архімеда .

Р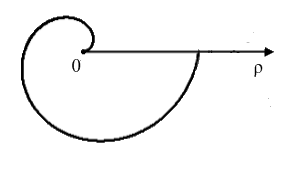 озв’язання

Обчислимо : , тоді

, де .

Тоді .

Обчислимо інтеграл:

=

.

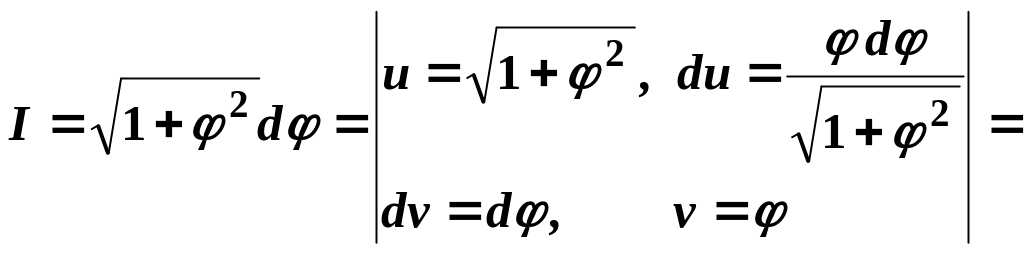
Тобто отримали: , звідки

.

Маємо:

.

Завдання для самостійної роботи

Обчислити довжини дуг ліній:

1. від до ; 2. , ;

3. , ;

4.

5.

Лекція № 28

Тема: Диференціал довжини дуги. Кривизна кривої. Коло кривизни. Еволюта. Евольвента.

План лекції: