Розв’язання

Побудуємо дані гіперболу та пряму. Д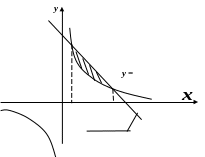 ля знаходження абсцис точок перетину графіків розв’яжемо систему рівнянь:

, тоді , , , звідки .

Отже,

кв. од.

8. .

Розв’язання

Побудуємо дані лінії.

Т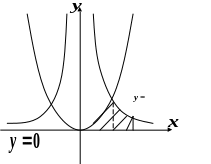 очки перетину графіків:

, тоді , , звідки .

Як бачимо, фігура розташована у I чверті, тому оберемо . На відрізку фігура зверху обмежена спочатку графіком функції (якщо ), а потім графіком (якщо ). Тому площу всієї фігури знайдемо як суму двох площ, кожну з яких обчислимо за формулою (3.1).

А саме: ,

де кв. од., кв. од.

Отримаємо: кв. од.

Перейдемо до розглядання прикладів обчислення площ у параметричній системі координат для циклоїди та кардіоїди. Обидві ці криві мають механічне походження та описуються точкою кола радіуса , що котиться без ковзання по деякій лінії. Для циклоїди цією лінією буде пряма, а для кардіоїди – знов коло радіуса , що має із першим колом зовнішній дотик.

9. Знайти площу фігури обмеженої віссю та однією аркою циклоїди

.

Розв’язання

Поглянемо на вигляд цієї кривої.

Параметр буде змінюватися від до . Використавши формулу (3.5), маємо:

кв. од.

Таким чином, площа однієї арки циклоїди втричі більше площі кола, що котиться.

10. Знайти площу, обмежену кардіоїдою ,

.

Розв’язання

Наведемо вигляд цієї кривої.

К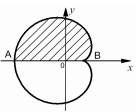 рива симетрична відносно осі . Обчислимо половину площі і подвоємо результат. Точкам та відповідають значення параметрів .

Для обчислення площі використаємо формулу (3.6).

Обчислимо : .

Тоді

.

Отримаємо: кв. од.

Тепер ознайомимося із цікавими кривими у полярній системі координат.

11. Обчислити площу, обмежену лемніскатою Бернуллі .

Розв’язання

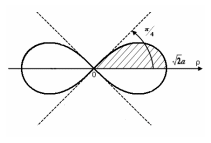
Прослідкуємо, як змінюється кут , коли радіус-вектор точки на лемніскаті описує чверть шуканої площі.

При , . Визна-чимо, чому дорівнює кут , коли радіус-вектор дорівнюватиме . Підставляючи в рівняння кривої, отримаємо: , , , звідки .

Таким чином, на чверті площі полярний кут змінюється в межах від до . Тоді за формулою (3.6):

.

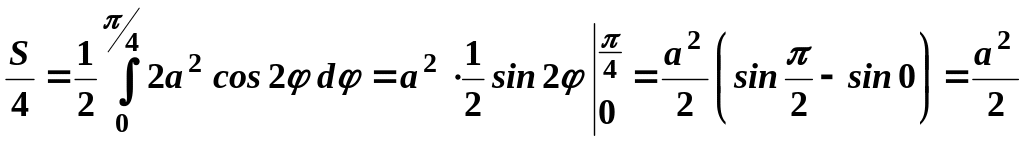Вся площа кв. од.

12.Обчислити площу однієї пелюстки рози, яка задається рівнянням .

Зауваження.

Зазначимо, що криві задані рівняннями (або ), де та - постійні величини, називаються розами. Якщо - парне число, то крива має - пелюсток, якщо - непарне число, то крива має - пелюсток.

Щоб знайти площу однієї пелюстки, визначимо, як змінюється полярний кут , коли радіус-вектор описує цю площу.

Нехай . Тоді , звідки .

При , при . Тобто кут змінюється від до .

Розв’язання

П

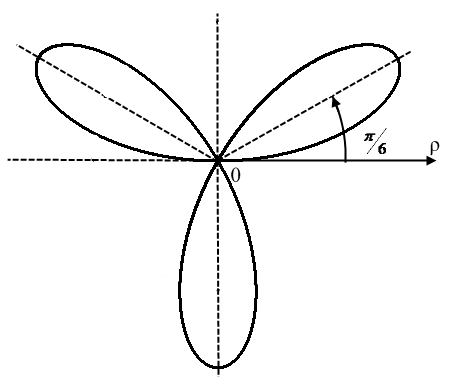
овернемось до нашого прикладу: - 3-х пелюсткова роза.

Описуючи площу однієї пелюстки, радіус-вектор пробігає кут від до .

Тоді

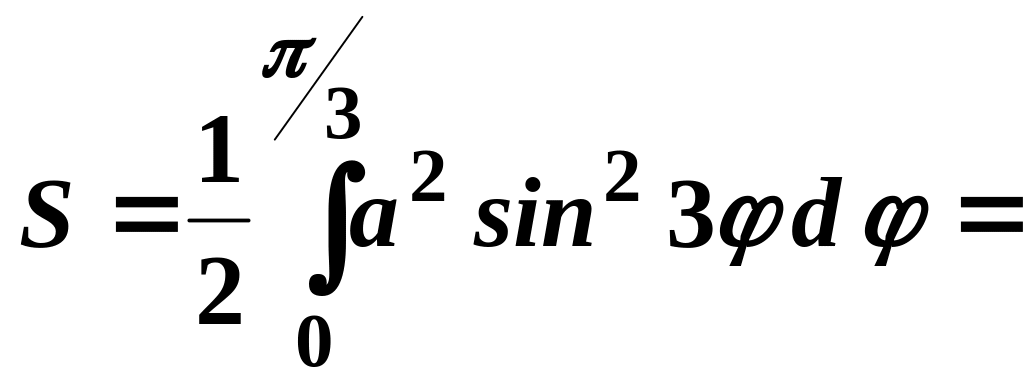
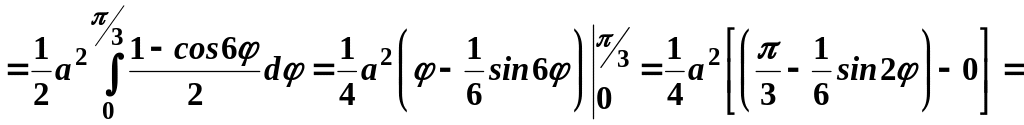
кв. од.

13.Обчислити площу, обмежену петлею декартового листа, який визначається рівнянням .