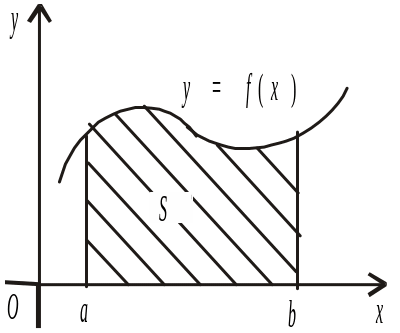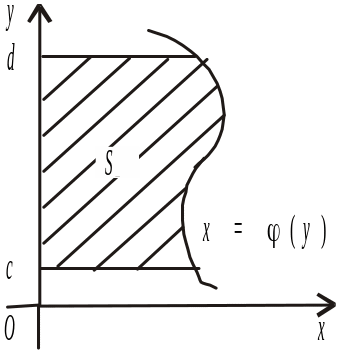§4. Формула інтегрування частинами

При обчисленні визначених інтегралів часто користуються формулою інтегрування частинами:

. (22)

Виведемо цю формулу. Нехай функції і мають на відрізку неперервні похідні і .

Знайдемо похідну добутку

.

Тоді функція є первісною для функції .

Згідно з формулою Ньютона - Лейбніца

.

До інтеграла у лівій частині цієї рівності застосовуємо властивість визначеного інтеграла:

,

або

.

Звідси й дістаємо формулу (22).

Приклади

Обчислити визначений інтеграл

а) ; б) .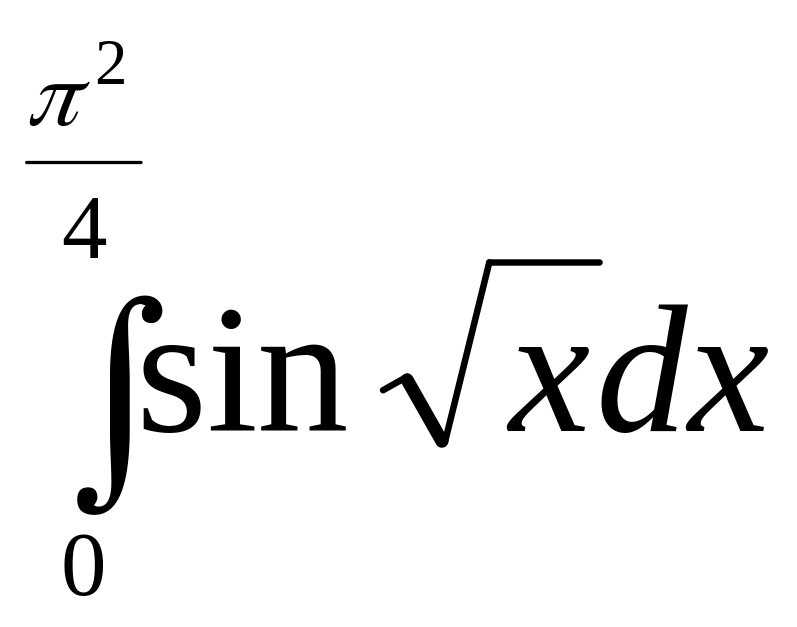

Розв’язання

а) Маємо , .Тоді , .

Отже, за формулою (22) дістаємо

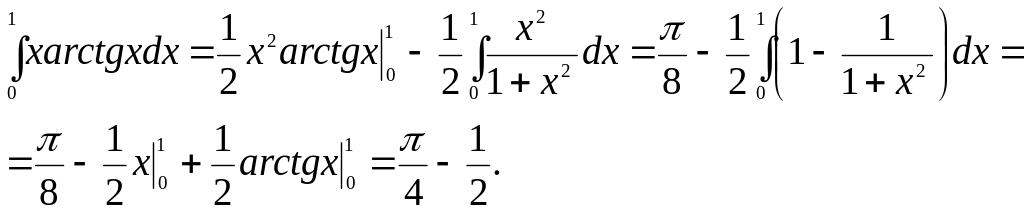
б) Застосовуємо спочатку підстановку . Тоді , і

.

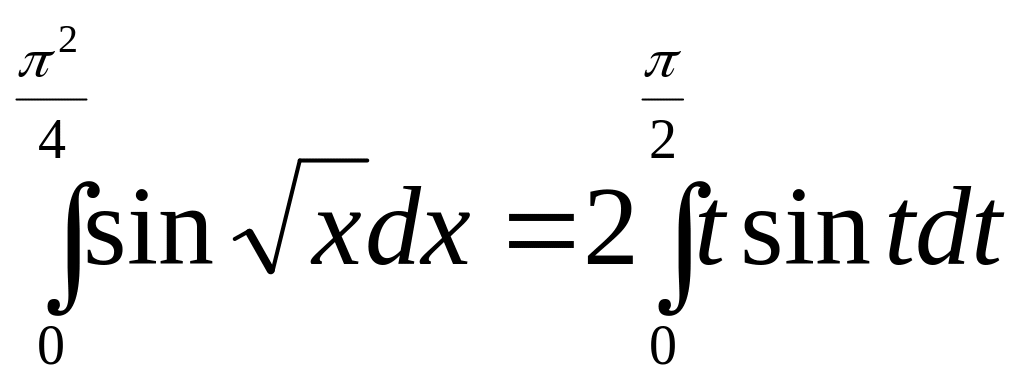До інтеграла в правій частині застосуємо формулу інтегрування. Нехай

, .

Тоді , .

Отже,

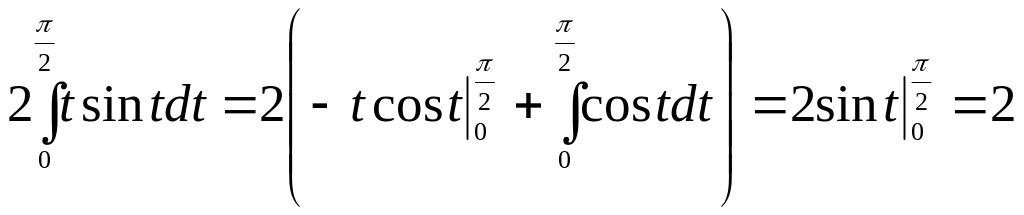
Лекція № 27

Тема: Застосування визначеного інтеграла до до обчислення площ плоских областей. Означення неперервної кривої. Спрямлювана крива. Застосування визначеного інтеграла до обчислення довжини плоскої кривої.

План лекції:

§1. Застосування визначеного інтеграла до до обчислення площ плоских областей.

§ 2. Означення неперервної кривої. Спрямлювана крива. Застосування визначеного інтеграла до обчислення довжини плоскої кривої.

§1. Застосування визначеного інтеграла до до обчислення площ плоских областей.

1). Обчислення площ плоских фігур в прямокутній системі координат

Якою б не була криволінійна фігура, що обмежена неперервними кривими лініями, шляхом її розсікання лініями паралельними осям координат, обчислення площі фігури можна звести до обчислення площ розглянутих нижче фігур.

І. Фігура обмежена лініями , y = 0, x = a, x = b (рис. 1). Функція — неперервна та Площа S такої криволінійної трапеції за геометричним змістом визначеного інтеграла така: .

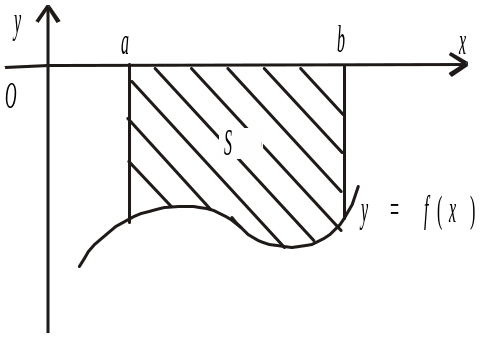
Якщо при виконанні всіх інших умов (рис. 2),

(27.1)

Рис. 1	Рис. 2	Рис. 3

ΙΙ.   Нехай фігура обмежена лініями (рис. 3). Функція — неперервна та Площа S такої фігури буде

(27.2)

Визначений інтеграл від додатної неперервної функції , заданої на відрізку , чисельно дорівнює площі криволінійної трапеції, обмеженої графіком функції і прямими (рис. 3.1):

. (27.1)

В разі, коли на (рис.3.2)

. (27.3)

y

Рис. 3.2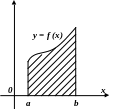

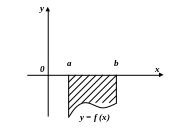
Рис. 3.1

Якщо функція на відрізку скінчене число разів змінює знак, то

.

Площу фігури, обмеженої кривими та і прямими за умови, що (рис.3.3) знаходять за формулою

. (27.4)

У випадку, коли фігура обмежена кривою та прямими (рис.3.4), її площу знаходять за формулою

. (27.5)

Якщо крива задана параметричними рівняннями , де - неперервні функції, що мають неперервні похідні на відрізку , то площа криволінійної трапеції, обмеженої цією кривою, прямими та відрізком осі , визначається за формулою:

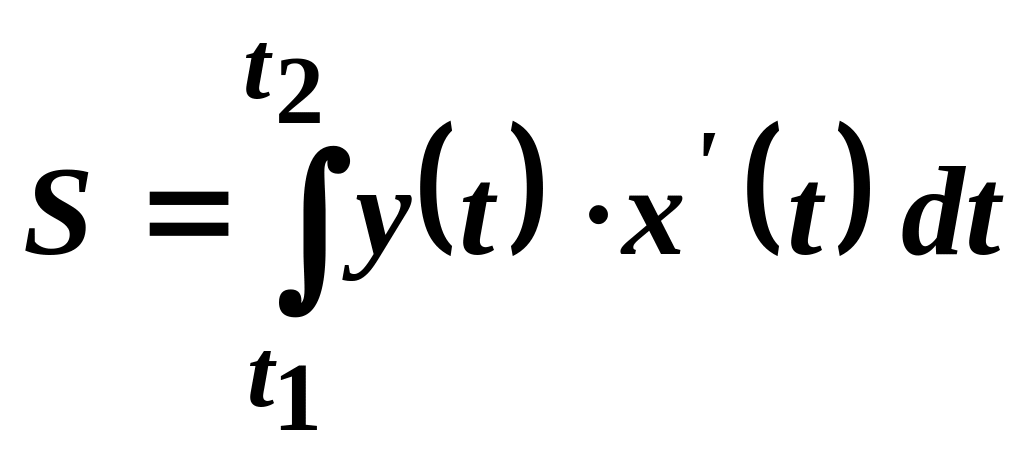, (27.6)

де і - значення параметра , при яких .

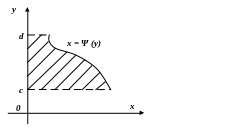
Рис. 3.3

Рис. 3.4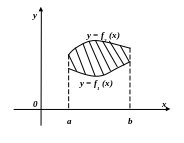

У полярній системі координат площа криволінійного сектора, обмеженого 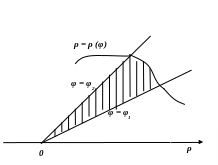неперервною кривою ,

та відповідними відрізками променів (рис. 3.5), дорівнює

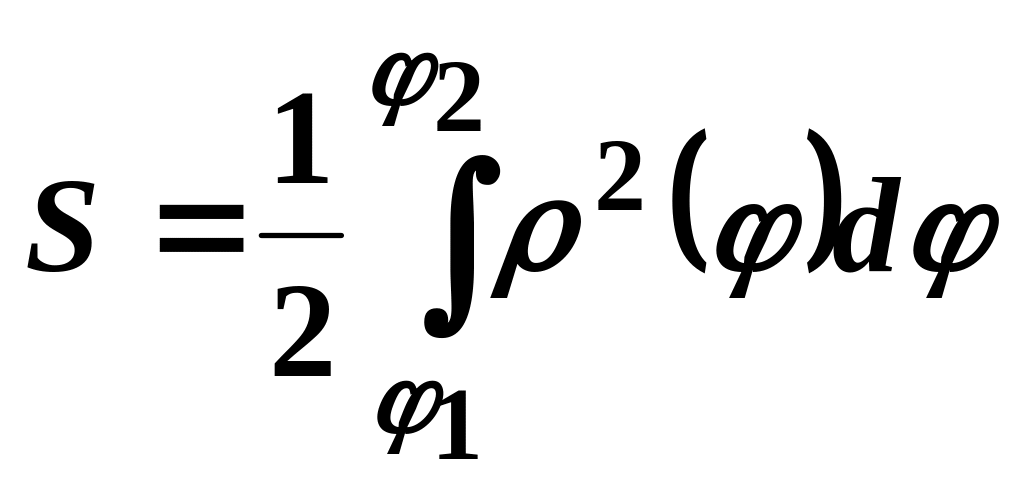. (27.7)

Рис. 3.5

Зразки розв’язування задач

Обчислити площі фігур, обмежених лініями.

1. .

Розв’язання

Побудуємо дані лінії і визначимо фігуру, площу якої треба знайти.

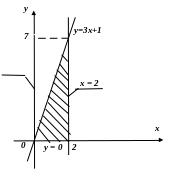
Площа визначається за формулою (3.1) :

x = 0

кв. од.

2. .

Розв’язання

Зобразимо фігуру, площу якої шукаємо.

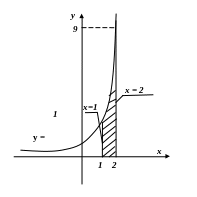
Тоді

кв. од.

3. .

Розв’язання

Фігура обмежена параболою і прямою .

Щ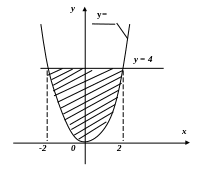 об визначити межі інтегрування, знайдемо абсциси точок перетину ліній та :

, звідки .

Як бачимо, фігура симетрична відносно осі , тому обчислимо площу її правої половини, а загальний результат подвоїмо.

Будемо мати: кв. од.

4. .

Розв’язання

Побудуємо дані лінії.

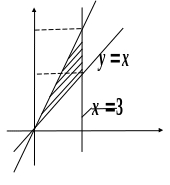Фігура на відрізку обмежена зверху , знизу прямою . Її площу знайдемо за формулою (3.3):

кв. од.

5. .

Розв’язання

Побудуємо параболу . Приведемо рівняння до канонічного виду, виділивши повний квадрат:

.

Отже, парабола має вершину в точці і перетинає вісь в точках .

Н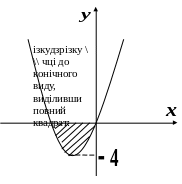 а відрізку функція має від’ємні значення. За формулою (3.2) шукана площа дорівнює:

кв. од.

6. .

Канонічний вид параболи :

тоді .

Парабола симетрична відносно прямої , має вершину .

Т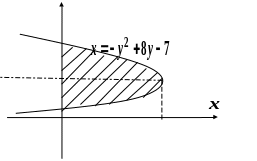 очки перетину з віссю :

, тоді

, звідки

, .

За формулою (3.4) знайдемо площу:

кв. од.

7. .