§ 2. Формула Ньютона – Лейбніца.

Якщо функція (16) є первісною для f(x), а функція F(x) будь - яка первісна для f(x), то справджується рівність

де С – довільна стала. Замість х підставимо в цю рівність а. Тоді

, звідси

Отже,

Поклавши в цій рівності x=b, дістанемо формулу Ньютона - Лейбніца

(18)

(тут замість t взято x).

Формула (18) виражає зв’язок між визначеним і невизначеним інтегралами, вона дає також змогу досить просто обчислювати визначений інтеграл від неперервної функції. Справді, якщо для f(x) відома яка - небудь первісна F(x), то визначений інтеграл дорівнює різниці двох значень первісної: при х=а і при х=b. Зокрема для тих функцій, невизначені інтеграли від яких беруться в скінченному вигляді, визначені і інтеграли можна можна обчислювати за допомогою формули (18).

Формулу Ньютона - Лейбніца записують ще так:

.

ПРИКЛАД

Обчислити визначені інтеграли:

а) б)

Р о з в ’ я з а н н я. Підінтегральні функції в кожному визначеному є функції, неперервні на відповідних відрізках. Тому для їх обчислення можна застосувати формулу Ньютона - Лейбніца.

а) Однією з первісних функцій для функції є . Отже,

.

б) Знайдемо будь - яку первісну для функції xlnx. Інакше кажучи, знайдемо

невизначений інтеграл (з точністю до довільної сталої)

.

Для знаходження цього інтеграла скористаємося формулою інтегрування частинами:

, , , ;

.

Тоді .

§3. Заміна змінної у визначеному інтегралі

При вивченні невизначеного інтеграла ми розглянули один з найбільш ефективних методів інтегрування функцій ― метод підстановки. Цим методом користуються також при обчисленні визначених інтегралів. Проте для визначеного інтеграла треба цей метод обґрунтувати. Доведемо таку теорему.

Теорема. Нехай виконуються умови:

1) неперервна функція на відрізку ;

2) функція і її похідна неперервні на відрізку ;

3) , і значення функції не виходять за межі відрізка при .

Тоді справджується рівність (19)

Доведення. Спочатку зазначимо, що в обох частинах рівності (19) інтеграли існують, бо підінтегральні функції неперервні на відповідних відрізках. Введемо допоміжні функції

; ;

; .

Легко бачити, що і мають похідні по , знайдемо їх. Функція є складеною. Продиференціюємо її:

.

Аналогічно .

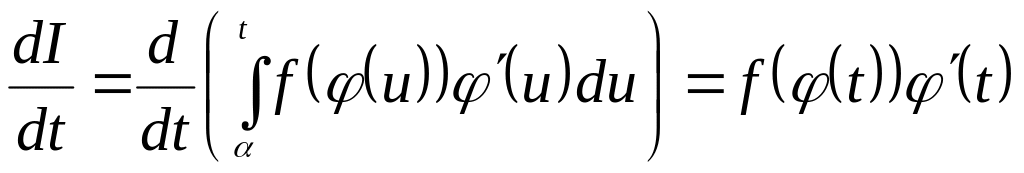Отже, похідні функцій і рівні між собою, тому функції відрізняються одна від одної на сталу величину

.

Ця рівність справджується для будь-якого . Нехай . Маємо

.

Як бачимо, , . Отже, . Тому .

Поклавши тут і врахувавши, що , дістанемо формулу (19). Теорему доведено.

Зауваження. Якщо при знаходженні невизначеного інтеграла методом підстановки у первісній функції ми від змінної поверталися до змінної (робили підстановку ), то при обчисленні визначеного інтеграла робити таку заміну немає потреби. Якщо вдається обчислити інтеграл, який міститься у правій частині формули (19), то цим самим обчислено і інтеграл лівої частини формули (19). На практиці, як і при знаходженні невизначеного інтеграла, найчастіше користуються підстановками виду . При цьому функція повинна задовольняти умовам: 1) має на відрізку неперервну похідну; 2) на відрізку вона є строго монотонною. Тоді така функція має обернену функцію , тобто маємо підстановку, про яку йдеться в теоремі. При цьому межі для знаходяться з рівності . Тоді є нижня межа по , а ― верхня межа.

Розглянемо окремий випадок формули (19), а саме, нехай маємо визначений інтеграл , який можна записати так:

.

У першому інтегралі застосовуємо поправку .

Очевидно, функція на відрізку задовольняє умови попередньої теореми. Отже,

.

Визначений інтеграл не залежить від того, якою буквою позначимо змінну інтегрування, тому в першому інтегралі замість візьмемо . Матимемо

.

Припустимо, що функція на відрізку є парною, тобто . Тоді з попередньої рівності дістаємо . (20)

Якщо на відрізку є непарною, , то .(21)

Приклади

Обчислити інтеграли:

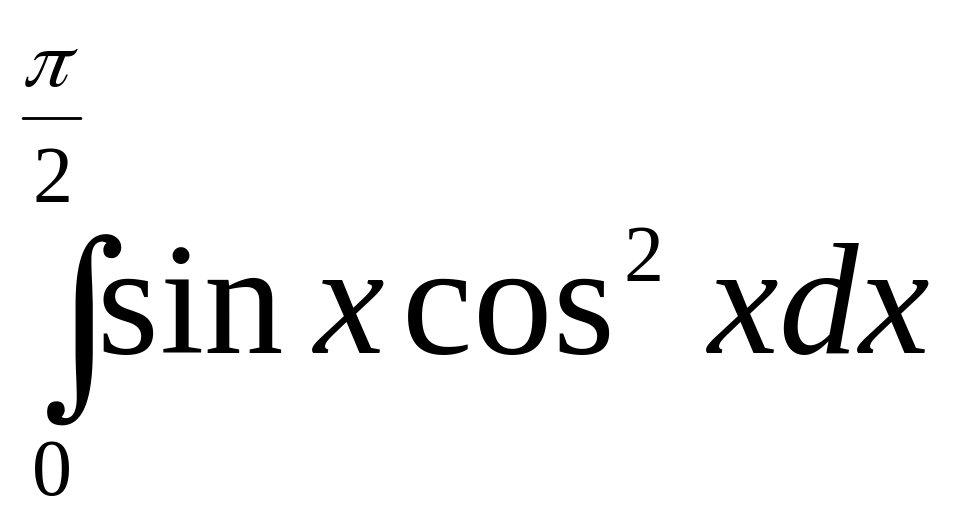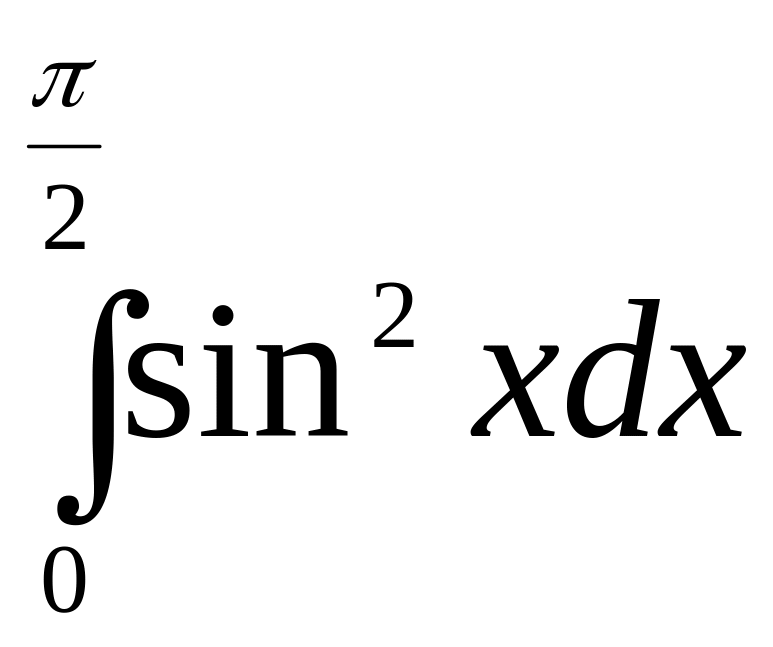а) ; б) ; в) ; г) .

Розв’язання

а) Застосовуємо підстановку , де .

Знайдемо межі для змінної (табл.2). Тоді ,

.

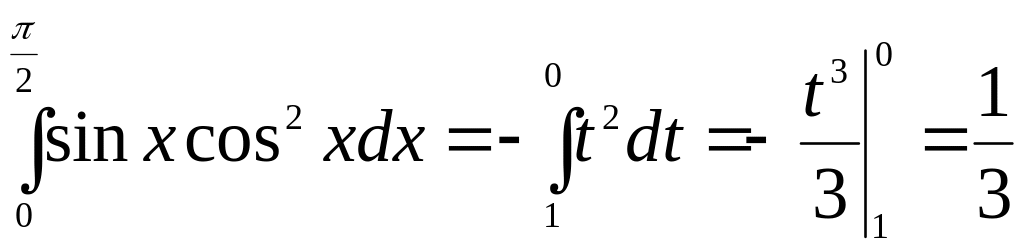б) Застосовуємо підстановку

.

Таблиця 2 Таблиця 3 Таблиця 4

Знайдемо межі по (табл.3).

Тоді . Отже,

.

в) Застосовуємо формулу

.

Тоді .

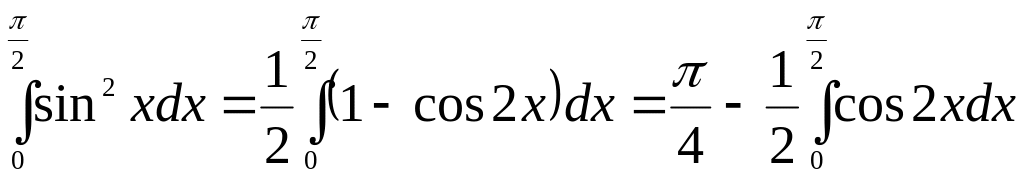Нехай . Знайдемо межі по (табл.4). Тоді .

Отже, .

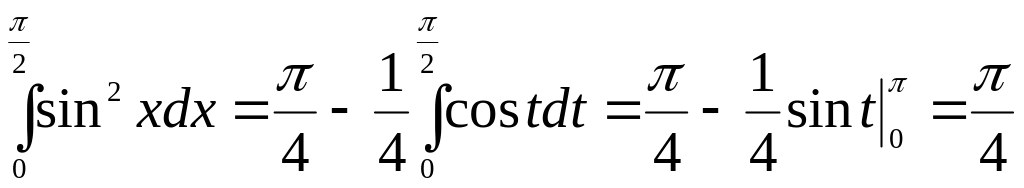г) Оскільки функція парна, то

.