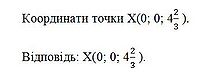Тема. Декартові координати у просторі.

План.

1. Введення декартових координат у просторі.Координати в просторі.

2. Координати середини відрізка. Відстань між точками в просторі. Довжина відрізка.

3. Координати точки при поділі відрізка в заданому відношенні.

4. Застосування координат в просторі.

     Декартова система координат у просторі задається трійкою попарно перпендикулярних осей (вісь ОХ – вісь абсцис, вісь ОУ – вісь ординат, вісь OZ – вісь аплікат), які мають спільний початок О (початок координат) і однаковий масштаб уздовж осей.

     Кожній точці простори за певним правилом ставиться у відповідність трійка чисел – абсциса, ордината та апліката (х;у;z). які називаються декартовими координатами точки. Ці координати визначаються в такий спосіб: через точку А проводимо три площини, паралельні координатним площинам YOZ, XOZ, XOY. Із координатними осями OX, OY, OZ площини перетнуться в точках х_А, у_А, z_A. Число х, абсолютна величина якого дорівнює довжині відрізка ОХ_А, називається абсцисою точки А. Це число буде додатним, якщо х_А належить додатній півосі ОХ, і від’ємним, якщо лежить на від’ємній півосі.

     Декартові координати у просторі записують у дужках поруч із буквеним позначенням точки А(х;у;z), причому першою в дужках стоїть абсциса, другою – ордината, третьою – апліката.

     Для точок площини ХОY апліката z дорівнює нулю, для точок площини XOZ – ордината у дорівнює нулю, для точок площини YOZ – абсциса х дорівнює нулю.

     Наприклад: точка А має координати 2;3;3, що записується так: А(2;3;3).

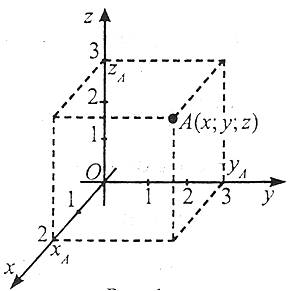
     Будь-якій трійці чисел х, у, z відповідає лише одна точка площини А(х;у;z).

     Приклад. Задано точки А(1;2;3), В(0;1;2), С(1;0;0), D(1;0;2). Які з цих точок лежать: 1) у площині XOZ; 2) на осі ОХ; 3) у площині YOZ?

Розв’язання

1. Якщо точка лежить у площині XOZ, то координата у дорівнює 0, у площині XOZ лежать точки С(1;0;0), D(1;0;2).

2. Якщо точка лежить на осі ОХ, то координата у і z дорівнюють нулю, отже, на осі ОХ лежить точка С(1;0;0).

3. У площині YOZ лежить точка В(0;1;2).

     Відповідь: 1) С, D; 2) С; 3) В.

Середина відрізка. Координати середини відрізка

В геометричних задачах часто можна зіштовхнутися з необхідністю знайти середину відрізку заданого координатами точок його кінців, наприклад в задачах пошуку медіани, середньої лінії, ...

Кожна координата середини відрізка дорівнює півсуммі відповідних координат кінців відрізку.

Ф ормула координат середини відрізка с кінцями a(xa, ya, za) та b(xb, yb, zb) на площині:

Формула відстані між двома точками A(xa, ya, za) и B(xb, yb, zb) в просторі:

Поділ відрізка в заданому відношенні

.

Нехай маємо дві точки   і потрібно знайти точку на відрізку  , яка ділить його у відношенні 

Координати точки  шукаємо за формулами

У випадку поділу відрізку пополам отримаємо відому формулу

Розвязування задач.

Задача 1. Заповніть пропуски  • Три попарно перпендикулярні прямі х, у, z , які перетинаються в точці О називаються … осями.  • Вісь х називається віссю … , вісь у називається віссю … , вісь z називається віссю … .  • Точка О - … .  • Кожна вісь точкою О розбивається на дві півосі - … , позначену стрілкою, і … .  • Площини ху, хz, уz називають … площинами.  • … точки записуватимемо в дужках поряд із позначенням точки А (х; у; z; ).  • Точки на осі х мають координати ( … ).  • Точки на осі у мають координати ( … ).  • Точки на осі z мають координати ( … ).  • Точки площини ху мають координати ( … )  • Точки площини уz мають координати ( … )  • Точки площини хz мають координати ( … ) 

З адача 2. Сторона куба дорівнює 10. Знайдіть координати його вершин. На дошці малюнок куба і система координат з початком в точці O. Переміщуючи початок координат в іншу вершину, розглянути варіанти знаходження координат вершин куба. 3. Як знайти координати середини відрізка, заданого в просторі?  4. Як знайти відстань між двома точками простору?  5. Заповнити таблицю.   Задача 3.

Доведіть, що чотирикутник АBCD є прямокутником, якщо А (5; -3; 2) , В(9;-1; 3), С (12; -5; -1), D(8; -7; -2).  Розв’язання  Паралелограм, діагоналі якого рівні, є прямокутником (ознака прямокутника). Якщо в чотирикутнику діагоналі точкою перетину діляться навпіл, то цей чотирикутник – паралелограм.  Отже, щоб довести, що чотирикутник АBCD , заданий координатами вершин, є прямокутником, треба:  - перевірити, що діагоналі точкою перетину діляться навпіл (тобто координати середини діагоналей однакові);  - перевірити, що діагоналі рівні.  Знайдемо координати середини діагоналі АС точки О за формулами 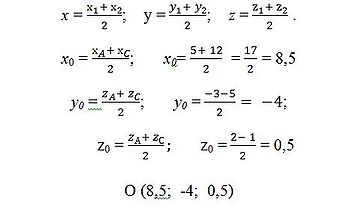   Координати середини діагоналей BD і АС однакові. Отже, АBCD - паралелограм. Тепер доведемо, що паралелограм АBCD є прямокутником. Перевіримо рівність діагоналей BD і АС. Знайдемо довжину діагоналі АС за формулою: 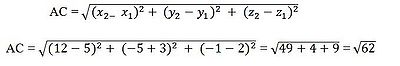 Знайдемо довжину діагоналі BD.    АBCD - паралелограм з рівними діагоналями, отже АBCD – прямокутник. Задача 4.

Точка М (2; 8; 5) – середина відрізка, кінці якого знаходяться на осі ОZ і в площині ХУ. Знайдіть координати кінців і довжину відрізка.  Розв’язання  Нехай точка М (2; 8; 5) – середина відрізка АВ. За умовою точка А знаходиться на осі OZ, отже її координати А (0; 0; z). Точка В знаходиться в площині ХУ, отже її координати В (х; у; 0). За формулами координат середини відрізка: 

 

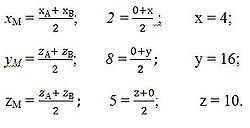
Отже, координати кінців відрізка АВ: А (0; 0; 10), В (4;16;0). Знайдемо довжину відрізка АВ за формулою: 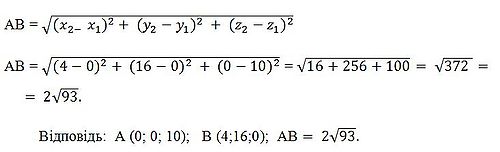 Задача 5 .

Знайдіть на осі z точку, яка рівновіддалена від точок А (6; -3; 2) і В (2; 4; -1).  Розв’язання  Нехай точка Х лежить на осі z, отже її координати Х (0; 0; z). За умовою точка Х рівновіддалена від точок А і В, отже  Знайдемо довжину відрізка АХ за формулою: 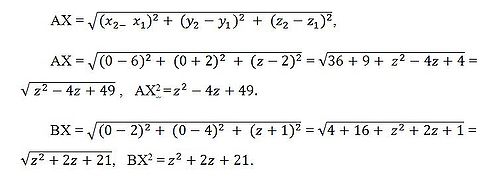 Прирівнюємо: