Раздел 5. Сетевое планирование управления.

Тема 5. Сетевые графики.

Занятие 1. ОСНОВНЫЕ ПОНЯТИЯ И ЭЛЕМЕНТЫ СЕТЕВОГО ГРАФИКА. ПРАВИЛА ЕГО ПОСТРОЕНИЯ и Оптимизации.

Время 2 часа.

1. ОСНОВНЫЕ ПОНЯТИЯ И ЭЛЕМЕНТЫ СЕТЕВОГО ГРАФИКА. ПРАВИЛА ЕГО ПОСТРОЕНИЯ.

При исследовании ПОД часто приходится встречаться с задачей рационального планирования сложных комплексных работ. Примерами таких работ могут быть: природоохранные мероприятия на нефтегазовом комплексе, при переработке и транспортировке нефти и т.д.

Характерным для таких процессов является то, что они состоят из ряда отдельных элементарных работ или «звеньев», которые не просто выполняются независимо друг от друга, а взаимно обусловливают так, что выполнение некоторых работ не может быть начато раньше, чем завершены некоторые другие.

Рациональное планирование ПОМ требует ответа на следующие вопросы:

-как распределить имеющиеся материальные средства и трудовые ресурсы между звеньями комплекса?

-в какие моменты начинать и когда заканчивать отдельные работы?

-какие могут возникнуть препятствия к своевременному завершению мероприятия и как их устранять? И т.д.

При планировании сравнительно небольших по объему комплексов работ ответ на такие вопросы обычно дает руководитель, при чем без специальных математических расчетов, просто на основе опыта и здравого смысла. Однако, когда речь идет об очень сложных, дорогостоящих комплексах ПОМ такие приемы становятся недопустимыми. Одним их математических методов, широко применяемых при решениях такого рода задач, является метод сетевого планирования управления. Метод СПУ позволяет наиболее полно и всесторонне учитывать особенности планируемых мероприятий и представляет собой достаточно простой и удобный инструмент для графического моделирования, анализа, оптимизации по определенным параметрам: раздельно по времени, людским ресурсам, трудозатратам, так и обобщенно по нескольким параметрам.

В основе СПУ лежит сетевой график, разработка которого базируется на теории ориентированных графов, теории вероятностей и математической статистике. Сетевой график (графическая модель) представляет собой сочетание событий и работ. Событие принято обозначать кружками, а работы - прямыми линиями со стрелками (рисунок 1).

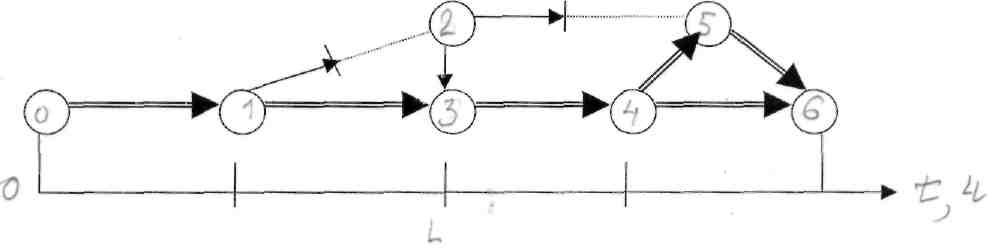Основные элементы сетевого графика следующие: событие, работа, путь.

Событие - это итог какой-то деятельности (работы), результат ее. Это не процесс и не требует затрат времени. Различают событие:

• исходное - факт начала всех работ (0);

• завершающее - это факт завершения комплекса работ (6);

• начальное - факт начала какой-то работы (i,j);

• конечное - факт окончания работы (i,j).

Работа. Под работой следует понимать:

• трудовой процесс, требующий затрат времени и ресурсов, называемый действительной работой;

• ожидание - это пассивный процесс, занимающий собой определенное время, но требующий затрат сил и средств;

• логическую связь между двумя событиями, взаимозависимость, не требующие затрат времени и ресурсов;

Такие работы называются фиктивными. На сетевом графике действительные работы и ожидания, обозначаются сплошными, ориентированными линиями, фиктивные - штриховыми. Работа обозначается а_ij, где i - начальное событие, j - конечное.

Путь - это любая непрерывная последовательность работ между какими-то событиями. Путь называется полным, если берется от исходного до завершающего события и обозначается L Таких путей на графике много. Длина каждого пути определяется как сумма продолжительностей действительных работ.

Полный путь максимальной продолжительности называется критическим. Он определяет общее время выполнения всего комплекса работ в целом. Все работы, лежащие на критическом пути называются критическими, т.е. узкими местами сетевого плана. Критический путь на графике выделяется двойной линией, утолщенной или цветной.

Если временные характеристики (времена работ) однозначны, неслучайны, то сетевые графики называются детерминированными, если случайны, то модель называется стохастической, а подход к ней вероятностным. Вероятностный подход удается свести к детерминированному путем расчета параметров математического ожидания работы и ориентированием ими как неслучайными. Графики строятся как правило, в масштабе времени, что более удобнее для управления всем ходом комплекса работ.

Прежде чем приступить к построению сетевого графика нужно составить перечень работ, свести их в таблицу с обязательным указанием:

• какие работы должны быть обязательно завершены, прежде чем начнется данная работа;

• какие работы могут быть начаты после завершения данной работы;

• какие работы могут выполняться параллельно с данной работой.

• График стоится слева направо. Первоначальный вариант графика стоится без учета масштаба времени, но с выполнением выше указанных условий. При этом необходимо избегать пересечения стрелок, добиваться минимально возможного числа функциональных связей - фиктивных работ.

Нужно придерживаться следующих правил и рекомендаций (рис. 2). На построенном графике:

• не должно быть «тупиков» (событие 7);

• не должно быть «хвостов» (событие 8);

• не должно быть замкнутых контуров (циклов), т.е. возвратов к наступившим событиям (событие 4, 5, 6, 7);

• не должно быть двух последовательных событий, связанных двумя работами (1,2). В таких случаях работы должны укрупняться, а время браться большее;

• события нумеруются слева направо, сверху вниз. Иногда в этих случаях используется правило о рангах.

Окончательный вариант сетевого графика строят с учетом масштаба времени и нумерация событий такого плана упрощается.

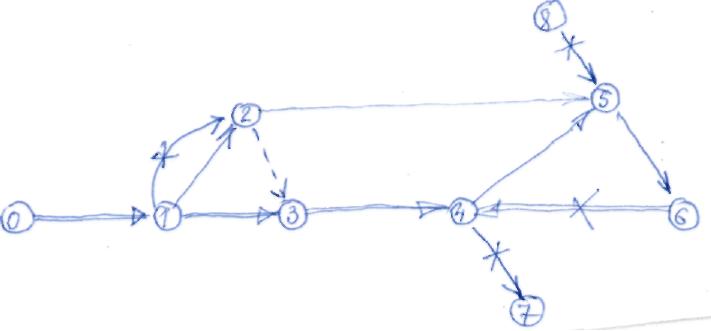
Рис.2

2. РАСЧЕТ ОСНОВНЫХ ПАРАМЕТРОВ СЕТЕВОГО ГРАФИКА И ЕГО ОПТИМИЗАЦИЯ

Основными параметрами сетевого графика являются: сроки выполнения работ, их продолжительность, продолжительности критического пути и резервы.

Продолжительность работы носит случайный характер. Поэтому ее целесообразно оценивать по максимальным и минимальным значениям. Максимальная оценка времени t_max (i,j) работы a_ij, называется пессимистической оценкой, а минимальная t_min(i,j) оптимистической. Иногда эти оценки называются экспертными.

Сетевые модели с однозначными временными оценками получили название детерминированных. К детерминированным моделям можно свести любой реальный процесс, если применить метод осреднения продолжительности работ и определить оценку ее математического ожидания и дисперсии (разброса).

Ожидаемая (планируемая) продолжительность работ t_ож и ее дисперсия σ² рассчитываются по формулам:

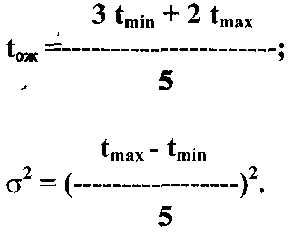
(1)

Значения времени наносят на график над линией работы, под ней дополнительно указывается количество трудовых, технических средств (ресурсов).

По графику определяют продолжительность путей, устанавливают критический путь L_Kp = L_max, t_Kp. Сравнивают это время t_Kp (как ранний срок выполнения всех работ) с заданным (директивным) временем τ_д, определяют внешний резерв сети R_BH

Теперь перейдем к расчету основных параметров сетевого плана.

Для этого подсчитаем аргумент функции Ф (z) по формуле

Вероятность выполнения работ в директивное время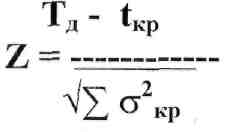

(2) По аргументу Z из математических таблиц определяем саму функцию Ф (z), являющуюся искомой вероятностью. Экспериментально установлено, что если эта вероятность мала, то слишком мала вероятность выполнения всех

работ в директивное время Т_д. Физически это означает, что t_кр ≈ T_ц. Если вероятность велика, то план получается неэкономным, так как T_ц.>> t_кр В таком случае задают меньшее значение Т_ц. Параметры событий:

Ранний срок свершения событий t_pi равен максимальной продолжительности путей а_m исходного события до i-гo. Записывается в левом секторе кружка (рис.3).

(3)

Поздний срок свершения события t_nj находится как разность между

продолжительностью критического пути t_Kp и максимальным путем от завершающего до данного i-ro события.

( 4)

Резерв времени события:

н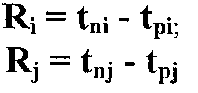 ачального-конечного -

(5)

Резерв R_i означает на какой дополнительной срок можно задержать свершение данного события i, не увеличивая t_Kp. Из этого следует, что события лежащие на критическом пути, резервов не имеют

R_iкр = 0

Значения позднего срока свершения события и его резерв указываются соответственно в правом и нижнем секторе кружка (рис.3)

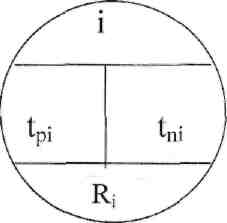
Р ис.3

Полный резерв работы (рис.4) находится их выражения

Исходя из рис.4 полный резерв работы

Полный резерв работы R_nij показывает, на какое максимальное время можно увеличить продолжительность данной работы (или задержать ее выполнение), чтобы при этом длина максимального из полных путей, проходящих через эту работу, не превышала критического пути t_Kp. В результате этого полный резерв работ, лежащих на критическом пути, равен нулю.

рис.4

При необходимости можно найти и другие параметры сети, например, свободный резерв, коэффициент напряженности сроков работ и т.п.

Оптимизация сетевого графика сводится к выбору оптимальных параметров сети в целях получения требуемой вероятности выполнения работ в директивное время, т.е. к построению различных вариантов планов и выбору

лучшего из них, когда t_Kp минимально.

Другими словами, оптимизация сводится к перераспределению работ между критическим путем и малозагруженными путями для уменьшения критического.

Однако при этом может оказаться, что критический путь изменится, и наиболее слабыми окажутся какие-то другие работы. Естественно предположить, что форсирование работ дается не даром, а требует вложения каких-то средств. Возникает типичная задача исследования операций: какие дополнительные средства, и в какие работы, следует вложить, чтобы больше заданной величины T_g, а расход дополнительных средств был бы минимальным?

Другая задача оптимизации относится к перераспределению уже имеющихся средств между отдельными работами. В некоторых случаях оказывается возможным, перебросив силы и средства с некритических участков плана на критические, добиться уменьшения суммарного времени его выполнения. Снова возникает типичная задача оптимизации: какие силы и средства надо перебросит с одних работ на другие для того, чтобы время выполнения комплексных работ стало минимальным?

Наконец, возможна еще одна постановка задачи оптимизации плана.

При наличии внешнего резерва времени сети R_Bн⁼ T_g — t_Kp, можно несколько растянуть работы для экономии некоторых средств. Возникает вопрос: до каких пределов можно увеличивать время выполнения работ и каких работ, чтобы полученная от этого экономия средств была максимальной? В такой постановке может ставиться задача оптимизации необязательно всего плана, а только отдельных некритических работ, имеющих временные резервы.

Использование ЭВМ. Если при случайных изменениях времен tjj меняется продолжительность критического пути, задача вычисления вероятности

P(t_кр ≤ T_g) = Ф(z) затрудняется и при большом числе работ расчеты становятся чересчур громоздкими. В этом случае эти вероятности удобнее определять методом Монте-Карло с использованием ЭВМ. При этом разыгрываются значения случайных величин t_ij и для каждой их совокупности значений определяется время t_ij тем способом, который применялся в детерминированном случае. Получив достаточно большое число N таких реализаций, мы можем непосредственно найти математическое ожидание, дисперсию величины t_ij. Что касается закона распределения, то в большинстве случаев для сложных сетей оказывается близким к нормальному. И вероятность выполнения плана в срок может вычислена по той же формуле.

Обычно при выполнении сложных комплексов работ первоначально намеченные планы не выполняются и их приходится по ходу работы пересматривать. При этом чрезвычайно удобно держать все данные о комплексе, варианты плана и поступающую информацию о его нарушении в памяти ЭВМ, которая по разработанному алгоритму оптимизирует план, указывая какие работы и в какой степени надо форсировать.

Метод статистических испытаний (Монте-Карло)

Все ранее рассмотренные методы построения математических моделей давали возможность установить аналитическую (формальную) связь между заданными условиями исследуемого процесса и исходом (результатом) его, характеризующимся одним или несколькими параметрами - показателями эффективности. Если в ход процесса вмешиваются случайные факторы, то он представляет собой стохастический процесс, а показатель эффективности -вероятность какого-то события или же математическое ожидание какой-то случайной величины. Иногда удается построить аналитическую модель случайного процесса (например, систему дифференциальных уравнений для вероятностей состояний или алгебраических уравнений для предельных вероятностей состояний) и связать заданные условия процесса с его исходом аналитическими зависимостями. Однако это удается далеко не всегда, '- главным образом, в тех случаях, когда случайный процесс, протекающий в - рассматриваемой системе, марковский или близок к нему.

На практике далеко не все случайные процессы, наблюдаемые в операциях, можно считать марковскими. Например, в реальных системах массового обслуживания поток заявок отнюдь не всегда является пуассоновским; еще реже наблюдается показательное (или близко к нему) распределение времени обслуживания. Для произвольных же потоков событий, переводящих систему из состояния в состояние, аналитические решения получены только для отдельных частных случаев, а в общем случае удовлетворительных методов математического описания соответствующих процессов не существует.

В тех случаях, когда построение аналитической модели явления по той

или другой причине трудно осуществить, применяется другой метод

моделирования, известный под названием метода статистических испытаний

или, иначе метода Монте-Карло (по названию города в княжестве Монако -

Франция).

Широкое распространение метода связано, главным образом, с передачей рутинных (громоздких) вычислительных операций ЭВМ.

Идея метода чрезвычайно проста и состоит она в следующем. Вместо того, чтобы описывать случайное явление с помощью аналитических зависимостей, производится и розыгрыш - моделирование случайного процесса с применением некоторой процедуры, дающей случайный результат. Так же как и в жизни конкретное осуществление процесса складывается каждый раз по иному, так же и в результате «розыгрыша» мы получаем один экземпляр - одну «реализацию» случайного явления. Произведя такую «имитацию» очень большое число раз, мы получим статистический материал - множество реализаций случайного явления-, который можно обработать обычными методами математической статистики.

Нередко такой прием оказывается проще, чем попытки построить аналитическую модель явления и исследовать зависимость между его параметрами на этой модели. Для сложных процессов, в которых участвует большое число элементов (машин, систем, людей, коллективов) и в которых случайные факторы непредвиденным образом взаимодействуют между собой, метод статистических испытаний, как правило, оказывается проще аналитического.

В сущности, методом «розыгрыша» может быть решена любая вероятностная задача; однако оправданным он становится только в случае, когда процедура «розыгрыша» проще, а не сложнее применения аналитических вычислительных методов.

Рассмотрим элементарный пример. Решается задача: в системе сточных вод имеется четыре комплекта фильтров, работающих независимо друг от друга. Вероятность отказа каждого из них р=0,5. Загрязнение водоема, куда сбрасываются отработанные воды, выше ПДК происходит при

одновременном выходе из строя двух комплектов фильтров. Определить вероятность загрязнения водоема.

Решим сначала задачу аналитически. Вероятность загрязнения водоема W вычислим через вероятность противоположного события - сохранения чистоты водоема. Вероятность сохранения водоема от загрязнения равна сумме вероятностей исправного состояния всех комплектов фильтров или выходе из строя одного.

Вероятность исправной работы всех фильтров равна 0,5⁴; вероятность выхода из строя одного равна C₄¹*0,5¹*0,5³ = 4*0,5⁴ следовательно W = 1-(0,5⁴+4*0,5⁴)≈0,688

Теперь попробуем решить эту же задачу «розыгрышем». Будем моделировать процедуру очистки воды с помощью другого, тоже случайного процесса. Вместо анализа состояния четырех комплектов фильтров будем бросать четыре монеты: появление герба будет условно означать выход из строя фильтра, решка - исправное его состояние. Если из четырех брошенных монет не менее двух упадут гербом, это будет означать, что произошло загрязнение водоема. Опытом или имитацией процесса в нашем случае будет бросание четырех монет, результатом (исходом эксперимента) - загрязнение водоема.

Повторим такой «опыт» очень много раз подряд. Тогда, согласно теореме Бернулли, частота «загрязнения» водоема почти наверняка будет мало отличаться от вероятности этого события W; значит, если мы бросим четыре монеты большое число раз N и разделим число «загрязнений» водоема на N, мы почти наверняка получим число, близкое к W, т.е. к 0,688.

В данном примере определение вероятности W розыгрышем было несравненно труднее, чем аналитическим расчетом. Очень часто однако оказывается, что получение вероятности события (или среднего значения случайной величины) аналитическим, расчетным путем настолько сложно и громоздко, что проще оказывается розыгрыш.

Другая задача. Произошел выброс хлора (аммиака) в количестве G. Известны метеоусловия (температура, состояние вертикальной устойчивость атмосферы), направление, скорость господствующего ветра. Определить вероятность заражения населенного пункта, находящегося на расстоянии L от предприятия. Несмотря на видимую простоту постановки задачи, ее аналитическое решение чрезвычайно сложно. Гораздо проще будет решать задачу «розыгрышем». Для этого надо «разыграть» координаты площади загрязнения с учетом исходных данных.

Таким образом, метод Монте-Карло есть прием математического моделирования случайных явлений, в которых сама случайность непосредственно включается в процесс моделирования и представляет собой его существенный момент. Каждый раз, когда в ход процесса вмешивается тот и другой случайный фактор, его влияние имитируется с помощью специально организованного «розыгрыша». Таким образом, строится одна реализация случайного явления, представляющая собой как бы результат одного «опыта». При большом числе реализаций интересующие нас характеристики случайного явления (вероятности, математические ожидания) находятся так же, как они определяются из опыта: вероятности - как частоты событий, математические ожидания - как средние арифметические значения соответствующих случайных величин.

Моделирование случайных явлений методом Монте-Карло имеет общие черты с процессом набора опыта отдельными людьми и человеческими коллективами. И тут, и там каждая отдельная реализация случайна; устойчивые закономерности обнаруживаются лишь при многократном наблюдении явления, при обширном опыте.

Большое число реализаций, требующееся при применении метода Монте-Карло, делает его вообще громоздким и трудоемким. Прежде чем применять этот метод, всегда имеет смысл попытаться решить задачу аналитически, и только если это не удается, прибегать к статистическому моделированию. Полезным оказывается хотя бы приближенное предварительное аналитическое решение задачи - это помогает выявить основные факторы, от которых зависит результат, и наметить план дальнейшей работы.

Моделирование случайных явлений методом Монте-Карло часто производится с целью проверки правомочности в данном случае того или иного математического аппарата, всегда основанного на некоторых допущениях. Пусть, например, рассматривая СМО, мы приближенно заменили не-пуассоновский поток заявок пуассоновским и непоказательное время обслуживания - полказательным. Моделирование того же процесса методом Монте-Карло покажет, допустимы ли эти упрощения, к каким ошибкам они приводят, и позволит ввести в расчетные формулы соответствующие поправки.

3. Единичный «жребий». Получение случайного числа.

Основным элементом, из совокупности которых складывается Монте-Карловская модель, является одна случайная реализация моделируемого явления, например, один выброс СДЯВ, один разрыв продуктопровода, выход из строя устройства безопасности спецоборудования.

Единичным жребием принято называть любой элементарный опыт, в котором решается один из вопросов:

а) Произошло или не произошло событие А?

б) Какое из возможных событий А₁ А₂,...,А_n произошло?

в) Какое значение приняла случайная величина X?

г) Какую совокупность значений приняла система случайных величин X₁, Х₂,..., Х_к?

Каждая реализация случайного явления состоит из цепочки единичных жребиев, перемежающихся обычными расчетами. Расчетами учитывается влияние исхода единичного жребия на ход процесса (в частности, на условия, в которых будет осуществляться следующий единичный жребий).

При любой организации единичного жребия должен быть пущен в ход какой-то механизм случайного выбора (бросание монет, костей, вынимание жетона из вращающегося барабана, числа из набора чисел, рулетка и т.п.). способы самые разнообразные, но назначение одно: получить величину R, распределенную с постоянной плотностью от 0 до 1.

Например, нам нужно получить ответ на вопрос «Какое из нескольких возможных событий появилось?»

Пусть имеется полная группа несовместных событий А₁ А2,...,А_К с вероятностями рь р₂,...,р_к. Так как события несовместны и образуют полную группу, то p₁ + р₂ +... +р_к ⁼ 1. Разделим весь интервал от 0 до 1 на К участков длиной рь р₂,...,р_к (рис.1).

Рис Л

Если случайное число R, выданное стандартным механизмом, попало, пример, на участок р₃, это означает, что появилось А₃.

В настоящее время при широком использовании ЭВМ для выбора учайного числа от 0 до 1 могут применяться датчики случайных чисел, [числительные алгоритмы для получения «псевдослучайных чисел». Так называется числа, получаемые по правилу построенному так, чтобы знаки 0 и 1 встречались одинаково часто, и, кроме того, чтобы зависимость как между отдельными знаками, так и между сформированными из них многозначными числами практически отсутствовала. Например, можно перемножить два произвольных n-значных двоичных числа a₁ и а₂ и из произведения взять n средних знаков - это будет число аз; затем перемножить а₂ и а₃ и повторить процедуру и т.д.

К достоинствам псевдослучайных чисел относится то, что они допускают возможность вторичного контрольного просчета той же самой реализации случайного процесса; другие способы формирования случайных чисел (физические датчики) этой возможности не дают.

4. Оценка точности характеристик, полученных методом Монте-Карло. Необходимое число реализаций.

Метод статистических испытаний основан на предельных теоремах вероятностей, утверждающих, что при большом числе опытов N частоты события приближается к его вероятности, а среднее арифметическое наблюдаемых значений случайной величины - к ее математическому ожиданию. Естественно встает вопрос — насколько велика будет ошибка, возникающая от такой приближенной замены? И какое должно быть число итераций N для того, чтобы эта ошибка с практической достоверностью не вышла за данные пределы. Другими словами необходимо определить точность характеристик случайного явления, полученных методом Монте-Карло.

Свои рассуждения будем основывать на центральной предельной теореме теории вероятностей. Согласно этой теореме, при большем числе опытов N их средний результат (частота Р события А или среднее арифметическое Х_ср наблюденных значений случайной величины X) распределяется приближенно по нормальному закону.

Приведем относящиеся сюда формулы.

а) Закон распределения частоты события при большом числе опытов.

Если проводится большое число независимых опытов N, в каждом из которых событие А появляется с вероятностью Р, то частота события А -

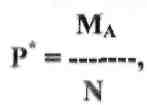
где М_A - число попаданий события А в N опытах

М_Л распределяется по нормальному закону с математическим ожиданием m_р*=Р и средним квадратичным отклонением

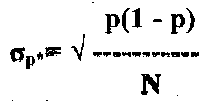
б) Закон распределения среднего арифметического при большом числе N.

Если при N независимых опытах, случайная величина X принимает значения: Х₁ Х₂,..., X_N, то среднее арифметическое этих значений:

Распределяется по нормальному закону, с математическим ожиданием m_х =m_х и средним квадратичным отклонением σ_х = о_х / √N

Поставим обратную задачу: сколько опытов N нужно произвести для того, чтобы с практической уверенностью ожидать, что частота отклонится от вероятности не больше, чем на заданную величину?

Для определения N, задаются каким-нибудь достаточно близким к 1 значением вероятности Q называемым «уровнем доверия» (0,95; 0,99; 0,995).

Приравниваем этому значению правую часть выражения

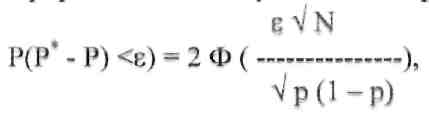
где Ф - функция Лапласа (табулирована) и разрешаем уравнение относительно N.

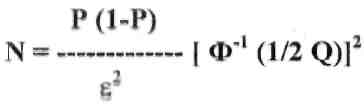
Если N оказывается не целым, его надо округлить в большую сторону до ближайшего целого (значение ε задается в пределах 0,01 - 0,05 в зависимости от уровня доверия Q).

Для оценки точности характеристик, полученных методом Монте-Карло пользуются распределением *******. Ввидусложности…………. для практических целей используются таблицы.