
- •1. Предел функции.
- •2. Односторонние пределы функций.
- •Задания для самостоятельной работы.
- •Свойства пределов функций.
- •4. Бесконечно малые и бесконечно большие функции.
- •5. Некоторые приемы вычисления пределов
- •1) Неопределённость вида . Отношение многочленов.
- •Задания для самостоятельной работы.
- •2) Неопределённость вида , содержащая иррациональность.
- •Задания для самостоятельной работы.
- •3) Неопределённость вида . Отношение многочленов. Иррациональность.
- •Задания для самостоятельной работы.
- •6. Непрерывность функции в точке.
- •Задания для самостоятельной работы.
- •7. Первый замечательный предел.
- •Задания для самостоятельной работы.
- •8. Второй замечательный предел.
- •Задания для самостоятельной работы.
Задания для самостоятельной работы.
1.
 2.
2.
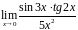
3.
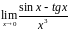 4.
4.
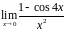
5.
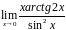 6.
6.
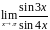
7.
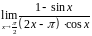 8.
8.
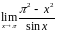
9.
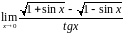 10.
10.
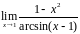
8. Второй замечательный предел.
Непрерывность
показательной функции
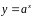 и логарифмической функции
и логарифмической функции
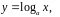
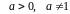 ,
а также теорема о непрерывности сложной
функции позволяют утверждать, что
степенно-показательная функция
,
а также теорема о непрерывности сложной
функции позволяют утверждать, что
степенно-показательная функция
 непрерывна всюду в области определения
и
непрерывна всюду в области определения
и
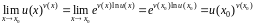 .
.
Пример
1.
Найти а)
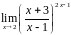 ;
б)
;
б)
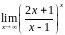 ;
в)
;
в)
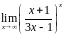 .
.
Решение.
а)
При
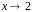 основание
основание
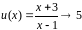 ,
показатель
,
показатель
 .
Поэтому
.
Поэтому
= .
.
б)
При
основание
 ,
показатель
,
показатель
 :
:
 .
.
в)
При
основание
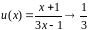 ,
показатель
:
,
показатель
:
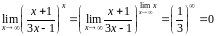 .▲
.▲
Особый
интерес представляют случаи, когда при
вычислении предела степенно-показательной
функции получаем неопределённость вида
 ,
,
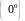 или
или
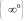 .
Неопределённость вида
(т.е. основание
.
Неопределённость вида
(т.е. основание
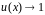 ,
а показатель
,
а показатель
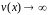 )
раскрывается с помощью второго
замечательного предела.
)
раскрывается с помощью второго
замечательного предела.
Теорема.
Предельное
значение функции
 при
существует и равно e
(второй замечательный предел):
при
существует и равно e
(второй замечательный предел):
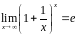 (1)
(1)
Следствие 1. Второй замечательный предел можно записать и в виде
 (2)
(2)
Пример
2.
Вычислить
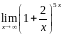 =
.
=
.
Решение.
Здесь
при
основание
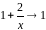 ,
показатель
,
показатель
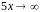 ,
поэтому воспользуемся вторым замечательным
пределом в форме (1):
,
поэтому воспользуемся вторым замечательным
пределом в форме (1):
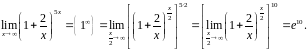 ▲
▲
Пример
3.
Вычислить
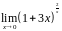 =
.
=
.
Решение.
Здесь при
основание
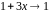 ,
показатель
,
показатель
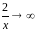 ,
поэтому воспользуемся вторым замечательным
пределом в форме (2):
,
поэтому воспользуемся вторым замечательным
пределом в форме (2):
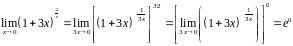 .▲
.▲
Формулам
(1) и (2) можно придать другой вид. При
стремлении аргумента
к некоторому значению
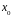 основание
,
значит, его можно представить в виде
основание
,
значит, его можно представить в виде
 ,
где
бесконечно малая в точке
функция. Чтобы воспользоваться вторым
замечательным пределом в виде (1) или
(2), надо в показателе иметь бесконечно
большую в точке
функцию
,
где
бесконечно малая в точке
функция. Чтобы воспользоваться вторым
замечательным пределом в виде (1) или
(2), надо в показателе иметь бесконечно
большую в точке
функцию
 :
:
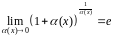 (3)
(3)
Пример
4.
Вычислить
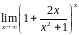 =
.
=
.
Решение.
Основание
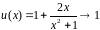 при
,
здесь
при
,
здесь


бесконечно малая функция при
.
Чтобы воспользоваться формулой (3), надо
в показателе поставить бесконечно
большую функцию
=
бесконечно малая функция при
.
Чтобы воспользоваться формулой (3), надо
в показателе поставить бесконечно
большую функцию
=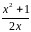 :
:
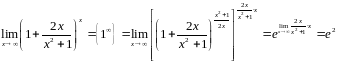 ,
,
так
как
 .▲
.▲
Пример
5.
Вычислить
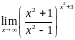 =
.
=
.
Решение.
Функция
 при
,
поэтому её можно представить в виде
при
,
поэтому её можно представить в виде
 =
=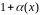 ,
при
:
,
при
:
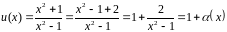 ,
,
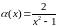 .
.
Значит,
в показателе надо поставить
=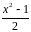 :
:
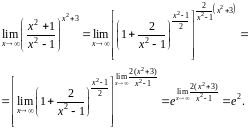
Здесь
учтено, что
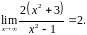 ▲
▲
Следствие
2.
Предельное
значение функции
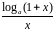 при
существует
и равно
при
существует
и равно
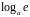 :
:
 . (4)
. (4)
В частности,
 . (5)
. (5)
Действительно,
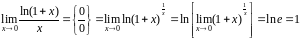 .
.
Пример
6.
Вычислить
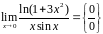 .
.
Решение.
Аргумент логарифма представлен в виде
суммы
,
где

бесконечно малая при
функция. Чтобы воспользоваться формулой
(5), надо логарифм разделить на
:
бесконечно малая при
функция. Чтобы воспользоваться формулой
(5), надо логарифм разделить на
:
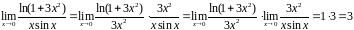 .
.
Здесь
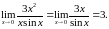 ▲
▲
Следствие
3.
Предельное
значение функции
 при
существует
и равно
при
существует
и равно
 :
:
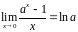 . (6)
. (6)
В частности,
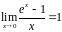 . (7)
. (7)
Действительно,
введём новую переменную
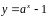

 ,
при
.
В силу формулы (4) получаем:
,
при
.
В силу формулы (4) получаем:
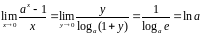 .
.
Пример
7.
Найти
 .
.
Решение.
Чтобы воспользоваться формулой (7), надо
в знаменателе записать бесконечно малую
в точке
функцию
 :
:
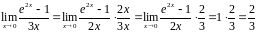 .▲
.▲
Пример
8.
Найти
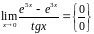 .
.
Решение.
Первый
способ.
Сначала представим числитель в виде
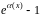 ,
а затем воспользуемся теоремой о пределе
произведения, формулой (7) и первым
замечательным пределом:
,
а затем воспользуемся теоремой о пределе
произведения, формулой (7) и первым
замечательным пределом:
 .
.
Второй способ. В числителе вычтем и прибавим единицу, в результате приходим к разности пределов:
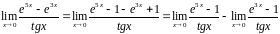 .
.
Найдем
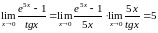
и
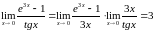 .
.
Теперь
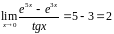 .
.
Пример
9.
Найти
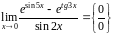 .
.
Решение. Прежде всего преобразуем числитель к виду , прибавляя и вычитая единицу:
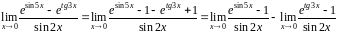 .
.
Остаётся вычислить
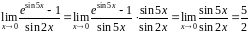 ,
,
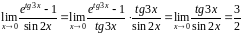 .
.
Значит,
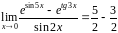 =1.
▲
=1.
▲
Замечание. Неопределённости вида и научимся раскрывать позже с помощью правила Лопиталя.
