
- •1. Предел функции.
- •2. Односторонние пределы функций.
- •Задания для самостоятельной работы.
- •Свойства пределов функций.
- •4. Бесконечно малые и бесконечно большие функции.
- •5. Некоторые приемы вычисления пределов
- •1) Неопределённость вида . Отношение многочленов.
- •Задания для самостоятельной работы.
- •2) Неопределённость вида , содержащая иррациональность.
- •Задания для самостоятельной работы.
- •3) Неопределённость вида . Отношение многочленов. Иррациональность.
- •Задания для самостоятельной работы.
- •6. Непрерывность функции в точке.
- •Задания для самостоятельной работы.
- •7. Первый замечательный предел.
- •Задания для самостоятельной работы.
- •8. Второй замечательный предел.
- •Задания для самостоятельной работы.
Задания для самостоятельной работы.
Записать на языке неравенств и дать геометрическую интерпретацию
1)
 при
при
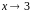 ,
,
2)
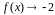 при
при
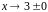 ,
,
3)
при
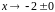 ,
,
4)
 при
при
 ,
,
5) при .
Свойства пределов функций.
Теорема.
Пусть
функции
и
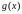 имеют пределы в точке
,
тогда функции
имеют пределы в точке
,
тогда функции
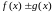 и
и
 также имеют пределы в точке
,
причем
также имеют пределы в точке
,
причем
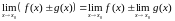 ,
,
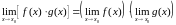 .
.
В
частности, для любого числа
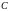
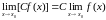 .
.
Теорема.
Если
функции
и
имеют пределы в точке
и
 ,
то функция
,
то функция
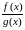 также имеет предел в точке
,
причем
также имеет предел в точке
,
причем
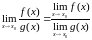 .
.
Теорема.
Пусть
существуют
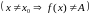 и
и
 ;
тогда в точке
существует предел сложной функции
(композиции)
;
тогда в точке
существует предел сложной функции
(композиции)
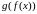 ,
причем
,
причем
 .
.
Эта
теорема позволяет вычислять пределы,
переходя от переменной
к новой переменной
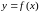 .
.
4. Бесконечно малые и бесконечно большие функции.
Определение. Функция называется бесконечно малой при , если
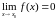 ,
,
т.е.
функция
называется бесконечно
малой при
,
если для любого
существует такое
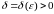 ,
что для всех
,
удовлетворяющих условию
,
что для всех
,
удовлетворяющих условию
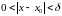 ,
выполняется неравенство
,
выполняется неравенство
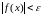 .
.
Таким
образом, если функция
 имеет
предельное значение
имеет
предельное значение
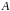 в точке
в точке
 ,
то есть
,
то есть
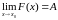 ,
то справедливо соотношение
,
то справедливо соотношение
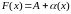 ,
где
,
где
 – бесконечна малая в точке
функция..
– бесконечна малая в точке
функция..
Определение.
Функция
называется бесконечно
большой при
,
если для любого
существует такое
,
что для всех
,
удовлетворяющих условию
,
выполняется неравенство
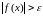 .
.
В этом случае будем писать
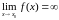 .
.
Заметим,
что функция
,
определенная и не равная нулю в некоторой
окрестности точки
,
кроме, быть может, точки
,
является бесконечно малой тогда и только
тогда, когда функция
 при
является бесконечно большой.
при
является бесконечно большой.
Сумма
(разность) и частное бесконечно больших
функций не обязательно являются
бесконечно большими функциями. Например,
и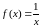 ,
и
,
и
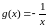 при
при
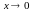
бесконечно большие функции, но их сумма
бесконечно большие функции, но их сумма
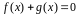 и при
и при
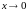 не является бесконечно большой функцией.
не является бесконечно большой функцией.
При
вычислении
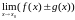 в случае, когда
и
бесконечно большие функции при
,
теоремы о пределе суммы и разности
функций неприменимы. В таких случаях
говорят, что при
выражение
в случае, когда
и
бесконечно большие функции при
,
теоремы о пределе суммы и разности
функций неприменимы. В таких случаях
говорят, что при
выражение
 представляет собой неопределенность
вида
представляет собой неопределенность
вида
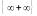 или
или
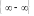 .
.
С
аналогичной ситуацией можем столкннуться
при вычислении предела частного
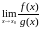 .
Будем говорить, что отношение
представляет собой при
неопределенность
вида
.
Будем говорить, что отношение
представляет собой при
неопределенность
вида
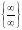 ,
если
и
бесконечно большие функции при
,
и
неопределенность
вида
,
если
и
бесконечно большие функции при
,
и
неопределенность
вида
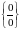 ,
если
и
бесконечно малые функции при
.
Вычисление пределов в этих случаях
называют “раскрытием
неопределенности”.
,
если
и
бесконечно малые функции при
.
Вычисление пределов в этих случаях
называют “раскрытием
неопределенности”.
5. Некоторые приемы вычисления пределов
1) Неопределённость вида . Отношение многочленов.
Пример
1.
Покажем, что в каждой точке
бесконечной прямой функция
 имеет предельное значение, равное
имеет предельное значение, равное
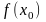 .
.
Решение.
Действительно,
в силу теоремы о пределе произведения
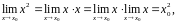 а в силу теоремы о пределе суммы
а в силу теоремы о пределе суммы
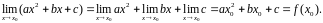 ▲ Пример
2.
Найти предел алгебраической дроби
▲ Пример
2.
Найти предел алгебраической дроби
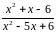 ,
когда
,
когда
а)
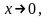 б)
б)
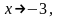 в)
в)
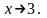
Решение. а). Согласно предыдущему
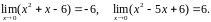
В силу теоремы о пределе частного (мы вправе её применить, т.к. предел знаменателя отличен от нуля) запишем:
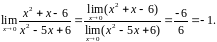
б).
В этом случае
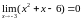 ,
т.е. в точке
,
т.е. в точке
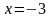 числитель
бесконечно малая функция.
числитель
бесконечно малая функция.
Найдем
предел знаменателя:
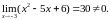
В результате получаем бесконечно малую в точке функцию:

в).
Здесь в точке
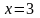 числитель имеет конечный и отличный
от нуля предел:
числитель имеет конечный и отличный
от нуля предел:
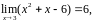 а знаменатель в этой точке
бесконечно малая функция:
а знаменатель в этой точке
бесконечно малая функция:
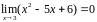 .
В результате получаем бесконечно большую
в точке
функцию:
.
В результате получаем бесконечно большую
в точке
функцию:
 ▲
▲
Пример
3.
Найти предел алгебраической дроби
при
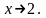
Решение.
Т.к.
и
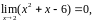 и
и
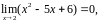 то получаем неопределённость вида
.
Непосредственно воспользоваться
теоремой о пределе частного не имеем
права. Поэтому сначала разложим квадратные
трёхчлены на множители и представим
дробь в виде
=
то получаем неопределённость вида
.
Непосредственно воспользоваться
теоремой о пределе частного не имеем
права. Поэтому сначала разложим квадратные
трёхчлены на множители и представим
дробь в виде
=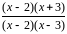 ,
а затем (вспоминая, что в определении
предела функции аргумент
,
а затем (вспоминая, что в определении
предела функции аргумент
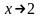 ,
но
,
но
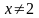 )
сократим на отличный от нуля множитель
)
сократим на отличный от нуля множитель
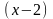 .
Окончательно получаем
.
Окончательно получаем
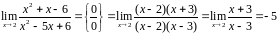 .▲
.▲
Пример
4.
Найти предел дроби
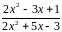 при
при
 .
.
Решение
.
Здесь,
как и в предыдущем примере, в точке
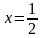 и числитель, и знаменатель являются
бесконечно малыми функциями:
и числитель, и знаменатель являются
бесконечно малыми функциями:
 .
.
Поэтому
выделим в числителе и в знаменателе
множитель
 ,
с полным правом
(
,
с полным правом
(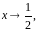 но
но
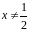 )
сократим на него и перейдём к пределу:
)
сократим на него и перейдём к пределу:
 .▲
.▲
Переходя к общему случаю, изучим поведение отношения двух многочленов
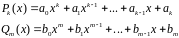
при
стремлении переменной
к конечному числу
 .
Повторяя рассуждения, приведенные в
примере 1, легко получить, что предельное
значение многочлена в точке
.
Повторяя рассуждения, приведенные в
примере 1, легко получить, что предельное
значение многочлена в точке
 существует и равно его частному значению
в этой точке:
существует и равно его частному значению
в этой точке:
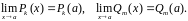

Поэтому
в случае
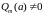 имеем право воспользоваться теоремой
о пределе частного:
имеем право воспользоваться теоремой
о пределе частного:
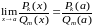 .
.
Если
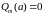 ,
но
,
но
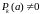 ,
то при приближении
к
отношение
,
то при приближении
к
отношение
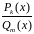 неограниченно
увеличивается:
неограниченно
увеличивается:
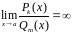 .
.
Нас
особенно интересует случай, когда и
 ,
и
,
т.е.
является нулем и числителя, и знаменателя.
Тогда
,
и
,
т.е.
является нулем и числителя, и знаменателя.
Тогда
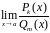 представляет собой неопределённость
вида
.
Согласно известной из алгебры теореме
Безу
многочлен,
который обращается в нуль при
,
делится без остатка на
представляет собой неопределённость
вида
.
Согласно известной из алгебры теореме
Безу
многочлен,
который обращается в нуль при
,
делится без остатка на
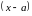 (верно и обратное утверждение). Значит,
для раскрытия неопределённости надо и
в числителе, и в знаменателе выделить
«носитель нуля»
бесконечно малую в точке
функцию
,
а затем сократить на этот множитель.
(верно и обратное утверждение). Значит,
для раскрытия неопределённости надо и
в числителе, и в знаменателе выделить
«носитель нуля»
бесконечно малую в точке
функцию
,
а затем сократить на этот множитель.
Пример
5.
Вычислить
 .
.
Решение.
И
в числителе, и в знаменателе «носителем
нуля» является множитель
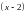 .
Выделим этот множитель. В числителе
вынесем за скобки
.
Выделим этот множитель. В числителе
вынесем за скобки
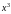 и представим разность квадратов как
произведение разности первых степеней
на сумму первых степеней:
и представим разность квадратов как
произведение разности первых степеней
на сумму первых степеней:
 .
.
В
знаменателе разность кубов представим
как произведение разности первых
степеней на неполный квадрат суммы:
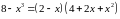 .
.
Получаем
 .
После сокращения на множитель
остается
.
После сокращения на множитель
остается
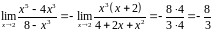 .▲
.▲
Пример
6.
Вычислить
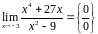 .
.
Решение.
И
в числителе, и в знаменателе «носителем
нуля» является множитель
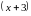 .
Выделим этот множитель в числителе:
.
Выделим этот множитель в числителе:
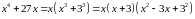 .
.
Здесь сумма кубов представлена как произведение суммы первых степеней на неполный квадрат разности.
В
знаменателе
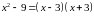 .
.
Получаем
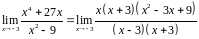 .
После сокращения на множитель
остается
.
После сокращения на множитель
остается
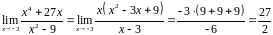 .▲
.▲
Пример
7.
Вычислить
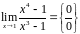 .
.
Решение.
И
в числителе, и в знаменателе «носителем
нуля» является множитель
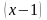 .
Выделим этот множитель в числителе:
.
Выделим этот множитель в числителе:
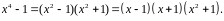
В
знаменателе:
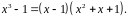
Значит,
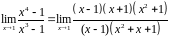 .
.
Сокращаем
на множитель
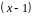 и вычисляем предел:
и вычисляем предел:
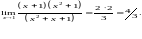 ▲
▲
Пример
8.
Вычислить
 .
.
Решение
В числителе множитель
можно выделить, разлагая
![]() по биному Ньютона:
по биному Ньютона:
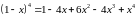 .
Тогда
.
Тогда
 .
.
После
сокращения на множитель
![]() получаем
получаем

Пример
9.
Вычислить

Решение . И здесь воспользуемся биномом Ньютона:
 .
.
Теперь легко выделить множитель и сократить на него:
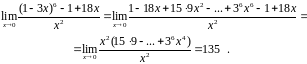 ▲
▲
