
- •1. Предел функции.
- •2. Односторонние пределы функций.
- •Задания для самостоятельной работы.
- •Свойства пределов функций.
- •4. Бесконечно малые и бесконечно большие функции.
- •5. Некоторые приемы вычисления пределов
- •1) Неопределённость вида . Отношение многочленов.
- •Задания для самостоятельной работы.
- •2) Неопределённость вида , содержащая иррациональность.
- •Задания для самостоятельной работы.
- •3) Неопределённость вида . Отношение многочленов. Иррациональность.
- •Задания для самостоятельной работы.
- •6. Непрерывность функции в точке.
- •Задания для самостоятельной работы.
- •7. Первый замечательный предел.
- •Задания для самостоятельной работы.
- •8. Второй замечательный предел.
- •Задания для самостоятельной работы.
1. Предел функции.
Определение
1 (Гейне).
Пусть
функция
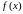 определена
на некотором интервале
определена
на некотором интервале
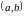 ,
кроме, быть может, точки
,
кроме, быть может, точки
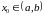 .
Число A
называется пределом функции
при
.
Число A
называется пределом функции
при
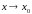 ,
если для любой последовательности
значений аргумента
,
если для любой последовательности
значений аргумента
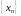 ,
сходящейся к
,
сходящейся к
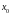 и такой, что
и такой, что
 ,
соответствующая последовательность
значений функции
,
соответствующая последовательность
значений функции
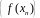 сходится к числу
сходится к числу
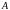 :
:
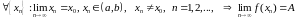 .
.
Тот
факт, что
есть предел функции
при
(в точке
 ),
будем записывать следующим образом:
),
будем записывать следующим образом:
 .
.
Из
определения следует, что значения
функции
в точках
 ,
лежащих вне некоторой окрестности точки
,
и значение функции в точке
не влияют ни на существование, ни на
величину предела функции
в точке
.
,
лежащих вне некоторой окрестности точки
,
и значение функции в точке
не влияют ни на существование, ни на
величину предела функции
в точке
.
Пример
1.
Покажем, что функция
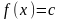 имеет предельное значение в каждой
точке
имеет предельное значение в каждой
точке
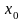 бесконечной прямой. В самом деле, для
любой сходящейся к
последовательности значений аргумента
бесконечной прямой. В самом деле, для
любой сходящейся к
последовательности значений аргумента
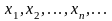 соответствующая последовательность
соответствующая последовательность
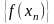 значений функции имеет вид
значений функции имеет вид
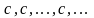 ,
т.е. сходится к
,
т.е. сходится к
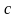 .
Значит, предельное значение функции
в любой точке
равно
.▲
.
Значит, предельное значение функции
в любой точке
равно
.▲
Пример
2.
Функция
 в каждой точке
бесконечной прямой имеет предельное
значение
.
Действительно, пусть
любая сходящаяся к
последовательность значений аргумента.
Соответствующая последовательность
значений функции имеет вид
,
т.е. сходится к
.
Значит, предельное значение функции
в любой точке
равно
.▲
в каждой точке
бесконечной прямой имеет предельное
значение
.
Действительно, пусть
любая сходящаяся к
последовательность значений аргумента.
Соответствующая последовательность
значений функции имеет вид
,
т.е. сходится к
.
Значит, предельное значение функции
в любой точке
равно
.▲
Пример
3.
Найти предел функции
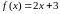 (рис.1) в точке
(рис.1) в точке
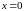 .
.
Решение.
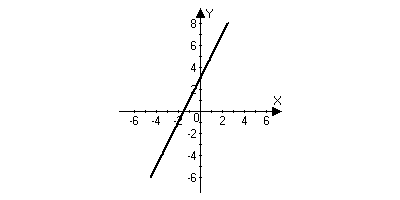 Будем
рассматривать данную функцию в некоторой
окрестности точки
,
например, на интервале
Будем
рассматривать данную функцию в некоторой
окрестности точки
,
например, на интервале
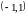 .
Функция определена всюду на указанном
интервале, в том числе и в точке
.
Возьмем какую-нибудь последовательность
значений аргумента
.
Функция определена всюду на указанном
интервале, в том числе и в точке
.
Возьмем какую-нибудь последовательность
значений аргумента

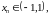
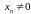 ,
,
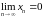 и рассмотрим соответствующую
последовательность значений функции
и рассмотрим соответствующую
последовательность значений функции
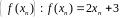 .
На основании теорем о пределе
последовательности имеем
.
На основании теорем о пределе
последовательности имеем
 .
.
Ввиду
произвольности выбранной последовательности
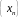 согласно определению предела функции
в точке
согласно определению предела функции
в точке
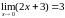 .▲
.▲
Пример
4.
Найти предел функции
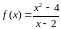 (рис.2) в точке
(рис.2) в точке
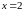 .
.
Решение.
В
точке
функция не определена.
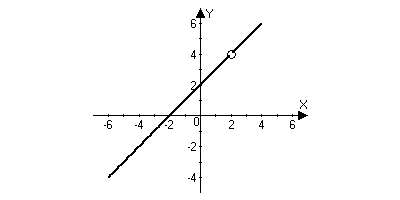 Будем
рассматривать функцию в некоторой
окрестности точки
,
например, на интервале
Будем
рассматривать функцию в некоторой
окрестности точки
,
например, на интервале
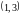 .
Возьмем какую-нибудь последовательность
значений аргумента
сходящуюся к точке
:
.
Возьмем какую-нибудь последовательность
значений аргумента
сходящуюся к точке
:
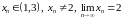 и рассмотрим соответствующую
последовательность значений функции
:
и рассмотрим соответствующую
последовательность значений функции
:
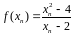 .
.
На основании теорем о пределах последовательностей имеем
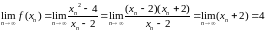
 .
.
Ввиду
произвольности выбранной последовательности
согласно определению предела функции
в точке
получаем
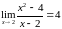 .
.
Заметим,
что функции
и
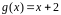 тождественны всюду, кроме точки
тождественны всюду, кроме точки
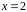 ,
где функция
,
где функция
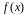 не определена.▲
не определена.▲
Для
того чтобы доказать, что функция
не имеет предела в точке
,
достаточно указать какую-нибудь
сходящуюся к
последовательность значений аргумента
чтобы соответствующая последовательность
значений функции
 не имела предела (или указать такие две
сходящиеся к
последовательности
и
не имела предела (или указать такие две
сходящиеся к
последовательности
и
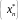 ,
что
и
,
что
и
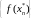 имеют разные пределы).
имеют разные пределы).
Пример
5.
Пусть
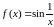 (рис.3). Выяснить, существует ли
(рис.3). Выяснить, существует ли
 .
.
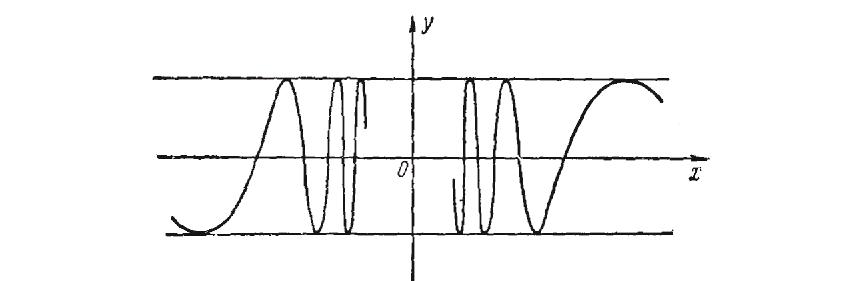
Р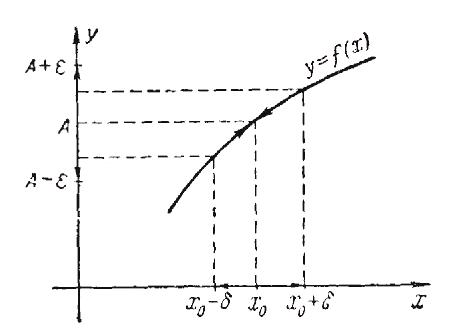 ешение.
Возьмем
две последовательности значений
аргумента
и
:
ешение.
Возьмем
две последовательности значений
аргумента
и
: и
и
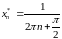 .
Очевидно,
.
Очевидно,
 ,
,
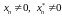 .
В точках последовательности
заданная функция
принимает
значение
.
В точках последовательности
заданная функция
принимает
значение
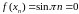 ,
а в точках последовательности
значение
,
а в точках последовательности
значение
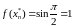 .
Поэтому
.
Поэтому
 ,
,
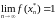 ,
то есть
,
то есть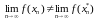 .
Значит,
не существует. ▲
.
Значит,
не существует. ▲
Определение
2 (Коши).
Пусть
функция
определена
на некотором интервале
,
кроме, быть может, точки
.
Число A
называется пределом функции
при
,
если для любого
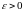 найдется
такое
найдется
такое
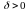 ,
что для всех
,
удовлетворяющих неравенству
,
что для всех
,
удовлетворяющих неравенству
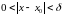 ,
выполняется неравенство
,
выполняется неравенство
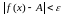 .
.
Это определение коротко можно записать с помощью кванторов:
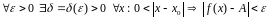 .
.
Пример
6.
Показать, что
 .
.
Решение.
Зададим
произвольное
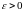 .
Мы должны найти такое
.
Мы должны найти такое
 ,
чтобы из неравенства
,
чтобы из неравенства
 вытекало неравенство
вытекало неравенство
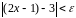 .
Преобразуем последнее неравенство:
.
Преобразуем последнее неравенство:

Решая
это неравенство относительно
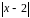 ,
находим
,
находим
 .
Значит, в качестве
.
Значит, в качестве
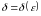 можно взять
можно взять
 (или любое меньшее число). В самом деле,
(или любое меньшее число). В самом деле,
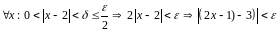 ,
,
а это согласно определению и означает, что .▲
Пример
7.
Самостоятельно показать, что
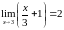 .▲
.▲
