1. Поняття про жорданову клітку

Определение. Жордановой клеткой порядка m, отвечающей собственному значению l, называется матрица вида:

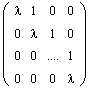     (2.1)

Иными словами, на главной диагонали такой матрицы располагается собственное значение l, диагональ, ближайшая к главной, сплошь занята единицами, а все остальные элементы матрицы равны нулю. Ниже даны примеры жордановых клеток соответственно первого, второго и третьего порядков: 

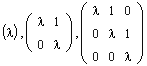
Определение. Блочно-диагональная матрица, на диагонали которой стоят жордановы клетки, называется жордановой матрицей: 

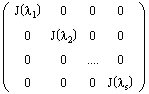     (2.2) ex2

Пример

Ниже представлена жорданова матрица, состоящая из трех жордановых клеток:  - размера 1, отвечающая собственному значению l₁=3;  - размера 2, отвечающая собственному значению l₂=4;  - размера 3, отвечающая собственному значению l₃=5. 

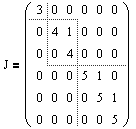
2. Анулюючий многочлен матриці або оператора

3. Мінімальний анулюючий многочлен

Многочлен ∆(z) з найнижчим степенем і старшим коефіцієнтом 1, який є анулюючим для оп. А наз. Мінімальним анулюючим многочленом оператора А (матриці А).

• Означ: ∆(z) Ǝ! і є дільником всіх інших анулюючих мн-ів оп. А Якщо А – дійсна матриця, то мін. анул. мн. теж дійсний! Д-ня: d(z)=НСД(f(z), g(z)) =>d(z) можна виразити через f(z), g(z) d(z)= f(z)р(z)+g(z)q(z) => якщо f(z), g(z) анулюючі, тоді і їх НСД – анул.

• Означ: Ǝ хоча б один анул. мн-н – характерист. P(z) ∆(z) - анул. мн-н мін. степеня з старшим коефіцієнтом 1, степінь ∆(z)<=n Д-ня: від супротивного : f(z) є анул. мін. мн А => f(z): ∆(z) припустимо, що f(z): ∆(z) => їх НСД має степ. менший, ніж степ. ∆(z) і теж анулюючий – Отримали протиріччя !

Єдиність – від супротивного : Нехай ∆1 – теж анулююч. мін. => ∆ : ∆1 і ∆1: ∆ => ∆1=c∆, c=1

• Теорема: Нехай ∆(z) – мін. анул. мног. А ; α – власне значення А  коли α – корінь ∆ Д-ня: Необхідність : α – власне знач. А h≠0 – відповідний власний вектор Ah= αh => A²h=A(Ah)= α²h 0=∆(A)h=∆( α)h => ∆( α)=0, тобто α – корінь Достатність: Нехай α – корінь ∆ => ∆(z)=(z- α)g(z), g(z)-неанул.

Ǝ x є V =.> g(A)x=y≠0 Ay= α Ey= αEy, тобто у- власний вектор , отже α- власне знач. А

4. Розклад лінійного простору на пряму суму підпросторів

— лінійний простір; , . Сума називається прямою (позичається ), якщо

; , , і цей розклад єдиний.

Приклади 1) і 2) є прикладами прямої суми, а 3) — ні.

Теорема 2. Лінійний простір розкладається у пряму суму своїх підпросторів тоді і тільки тоді, коли об’єднання базисів підпросторів є базисом всього .

Доведення. Нехай , а — базис , — базис .

, ; ;

;

, тобто система векторів

*)

є повною в .

Доведемо,що система *) — лінійно незалежна. Припустимо, що і є такі, що

. (1)

Вектор , який стоїть праворуч, можна представити у вигляді і цей розклад єдиний. Із (1) випливає:

, ,

а із лінійної незалежності базисів і :

і ,

що доводить норму частину теореми.

Тепер припустимо, що система *) — базис — пряма.

:

і цей розклад єдиний. Тобто , де . Це і доводить той факт, що сума — пряма. Теорему доведено.