§ 25. Инварианты поля

Из векторов напряженностей электрического и магнитного полей можно составить инвариантные величины, остающиеся не­изменными при преобразованиях от одной инерциальной систе­мы отсчета к другой.'

Вид этих инвариантов легко найти исходя из четырехмер­ного представления поля с помощью антисимметричного 4-тен­зора F^ik. Очевидно, что из компонент этого тензора можно со­ставить следующие инвариантные величины:

F_lkF^ik = inv, (25,1)

e^iklmF_ikF_lm = im, (25,2)

где е^Шт — совершенно антисимметричный единичный тензор (см. § 6). Первая из этих величин — истинный скаляр, а вто­рая — псевдоскаляр (произведение тензора F^ik на дуальный ему тензор)¹).

Выражая компоненты F^ik через компоненты Е и Н согласно (23,5), легко убедиться в том, что в трехмерной форме эти инварианты имеют вид

H²-E² = im,

ЕН = inv.

(25,3) (25,4)

Псевдоскалярность второго из них очевидна из того, что он представляет собой произведение полярного вектора Е на ак­сиальный вектор Н (квадрат же (ЕН)² будет истинным ска­ляром) .

Из инвариантности приведенных двух выражений вытекают следующие выводы. Если в какой-нибудь системе отсчета элек­трическое и магнитное поля взаимно перпендикулярны, т. е. ЕН =0, то они перпендикулярны и во всякой другой инерциаль­ной системе отсчета. Если в какой-нибудь системе отсчета абсо­лютные величины Е и Н равны друг другу, то они одинаковы и в любой другой системе.

Имеют, очевидно, место также и следующие неравенства. Если в какой-нибудь системе отсчета Е>Н (или £<Я), то и во всякой другой системе будет Е > Я (или Е < Я). Если в какой-либо системе отсчета векторы Е и Н образуют острый (или тупой) угол, то они будут образовывать острый (или ту­пой) угол и во всякой другой системе.

Преобразованием Лоренца можно всегда достичь того, чтобы Е и Н получили любые значения, удовлетворяющие только усло­вию, чтобы Е² — Н² и ЕН имели заданные определенные зна­чения. В частности, можно найти такую инерциальную систему отсчета, в которой электрическое и магнитное поля в данной точке параллельны друг другу. В этой системе ЕН = £Я, и из двух уравнений

Е* — Я² = £о— Но, ЕН = ЕоН$

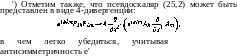можно найти значения Е и Н в этой системе отсчета (Е₀ и Но — электрическое и магнитное поля в исходной системе отсчета).

Исключением является случай, когда оба инварианта равны нулю. В этом случае Е и Н во всех системах отсчета равны по величине и взаимно перпендикулярны по направлению.

Если лишь ЕН = 0, то можно найти такую систему отсчета, в которой Е = 0 или Н = 0 (смотря по тому Е²—Н² <С или > 0), т. е. поле чисто магнитное или чисто электрическое; наоборот, если в какой-нибудь системе отсчета Е = 0 или Н = 0, то во всякой другой системе они будут взаимно перпендикулярны в соответствии со сказанным в конце предыдущего пара­графа.

Изложим еще и другой способ подхода к вопросу об инва­риантах антисимметричного 4-тензора. Этот способ делает оче­видным единственность двух независимых инвариантов (25,3—4) и в то же время выявляет некоторые поучительные математиче­ские свойства преобразований Лоренца в применении к 4-тен-зору.

Рассмотрим комплексный вектор

F = E + /H. (25,5)

Используя формулы (24,2—3), легко видеть, что преобразо­вание Лоренца (вдоль оси х) для этого вектора имеет вид

F_x = F'_x, F_y — F'_y ch ф — iF'_z sh ф = F' cos wp — F'_z sin /ф,

(25,6)

F_z = F_z cos /ф + F'_y sin др, Шф = —.

Мы видим, что вращение в плоскости xt 4-пространства (како­вым и является рассматриваемое прербразование Лоренца) для вектора F эквивалентно вращению на мнимый угол в плоскости yz трехмерного пространства. Совокупность же всех возможных поворотов в 4-пространстве (включающая в себя также и про­стые повороты осей х, у, z) эквивалентна совокупности всех воз­можных поворотов на комплексные углы в трехмерном простран­стве (шести углам поворота в 4-пространстве соответствуют три комплексных угла поворота трехмерной системы).

Единственным инвариантом вектора по отношению к поворо­там является его квадрат F² = E² — #² + 2г'ЕН. Поэтому ве­щественные величины Е² — Н² и ЕН являются единственными инвариантами тензора Fik.

Если F² ф 0, то вектор F можно представить в виде F = an, где п — единичный (n² = 1) комплексный вектор. Путем надле­жащего комплексного поворота можно направить п вдоль одной из координатных осей; при этом, очевидно, п станет веществен­ным и тем самым определит направления обоих векторов Е и Н: F = (£ + Ш) п. Другими словами, векторы Е и Н станут парал­лельными друг другу,

Задача

Определять скорость системы отсчета, в которой электрическое и маг* нитное поля параллельны.

Решение. Систем отсчета К', удовлетворяющих поставленному усло­вию, существует бесконечное множество: если найдена одаа из них, то тем же свойством будет обладать и любая другая система, движущаяся отно­сительно первой со скоростью, направленной вдоль общего направления по­ле* F. и Н. Поэтому достаточно определить ту из этих систем, скорость которой перпендикулярна к обоим полям. Выбирая направление скорости в качестве осе х и воспользовавшись тем, что в системе К поля Е_х — Н_х = 9, Е_уН'_г — E'jtt'y = 0, получим с помощью формул (24,2—3) для скорости V системы К.' относительно исходной системы следующее уравнение:

V/c

[EHJ

1 -f F²/c²

(из двух корней квадратного уравнения должен, разумеется, быть выбран тот,' для которого V < с).