1. Для частицы в поле коллапсара найти радиусы круговых орбит (с. А. Каплан, 1949).

^л) Построение системы отсчета, свободной от такой неполноты, будет рассмотрено в конце следующего параграфа.

Решение. Зависимость r(t) для частицы, движущейся в шварцшиль-довом поле, дается формулой (101,4) или, в дифференциальном виде:

1 — r_g/r с dt

^{1 йт 1} К-^²и]^1/2, (о

где

М¹ \Т/2

0,943

(т — масса частицы, r_B = 2km'lc² — гравитационный радиус центрального тела с массой т'). Функция U(r) играет роль «эффективной потенциальной энергии» в том смысле, что условием <g₀ ^ U(r) определяются (аналогично

Рис. 21

нерелятивистской теории) допустимые области движения. На рис. 21 изо­бражены кривые U(г) для различных значений момента частицы М.

Радиусы круговых орбит и соответствующие им значения ^ в Л( опре­деляются экстремумами функции U(r), причем минимумы отвечают устой­чивым, а максимумы — неустойчивым орбитам. Совместное решение уравне­ний U(r)=&₀, U'(r)= 0 дает:

Л1² Г / зИЩ1

причем верхний знак относится к устойчивым, а нижний — к неустойчивым орбитам. Ближайшая к центру устойчивая круговая орбита имеет пара­метры

г = Zr_g, М = л/з mcr_g, S₀ = д/у ^т°^г-

Минимальный радиус неустойчивой орбиты равен Зг_в/2 и достигается в пределе М-*-<», й?о-*-°°. На рис, 22 изображена кривая зависимости г\т_а от M/mcr_g; ее верхняя ветвь дает радиусы устойчивых, а нижняя — неустой­чивых орбит ¹).

2. Для движения в том же поле определить сечение гравитационного захвата падающих на бесконечности: а) нерелятивистских, б) ультрареля­тивистских частиц (я. Б. Зельдович, и. Д. Новиков, 1964).

Решение, а) Для нерелятивистской (на бесконечности) скорости v_M энергия частицы So « л*с²- Из кривых рис. 21 видно, что прямая Sо = т<?

Рис. 22 Рис. 23

лежит выше всех потенциальных кривых с моментами М < 2mcr_g, т. е. с прицельными расстояниями р < 2cr_g/v_ao. Все частицы с такими р грави­тационно захватываются: они достигают (асимптотически, при t-*-oo) шварц­шильдовой сферы, не уходя снова на бесконечность. Сечение захвата:

б) В уравнении (1) задачи 1 переход к ультрарелятивистской частице (или к лучу света) осуществляется заменой m -+■ 0. Введя также прицельное расстояние р = сМ1&_й, получим:

¹ ^л/^ + ^Л.

1 - r_s/r cdt V ¹ г^{2 +} г³ *

Границы движения по г (точки поворота) определяются нулями подкорен­ного выражения. Как функция от р они изображаются кривой на рис. 23; возможным движениям отвечает незаштрихованная часть плоскости. Кривая имеет минимум в точке

3 д/з 3

Р = -у-^, r = _Tr_g.

При меньших значениях прицельного расстояния частица не встречает точки поворота, т. е. проходит к шварцшильдовой сфере. Отсюда сечение захвата

27 ₂

') Напомним для сравнения, что в ньютоновском поле круговые орбиты были бы возможны (и устойчивы) на любом расстоянии от центра (радиус связан с моментом согласно г = M²jkm'm²),

§ 103. Гравитационный коллапс пылевидной сферы

Выяснение хода изменения внутреннего состояния коллапси-рующего тела (в том числе в течение процесса его сжатия под шварцшильдовой сферой) требует решения уравнений Эйнштей­на для гравитационного поля в материальной среде. В централь­но-симметричном случае уравнения поля могут быть решены в общем виде в пренебрежении давлением вещества, т. е. для уравнения состояния «пылевидной» материи: р = 0 (R. Tolman, 1934). Хотя такое пренебрежение в реальных ситуациях обычно недопустимо, общее решение этой задачи представляет замет­ный методический интерес.

Как было указано в § 97, пылевидная среда допускает выбор системы отсчета, являющейся одновременно синхронной и со­путствующей'). Обозначив выбранные именно таким образом время и радиальную координату посредством⁴ т и R, напишем сферически-симметричный элемент интервала в виде²)

ds² = dx² - <*• ®dR² - г² (т, R) (dQ² + sin² 9 dq>²). (103,1)

Функция r(x, R) представляет собой «радиус», определенный так, что 2пг есть длина окружности (с центром в начале коор­динат). Форма (103,1) фиксирует выбор т однозначным обра­зом, но допускает еще произвольные преобразования радиальной координаты вида R = R(R').

Вычисление компонент тензора Риччи для этой метрики при­водит к следующей системе уравнений Эйнштейна ³):

- <?-V² + 2т f + г² + 1 = 0, (103,2)

^{--^(2r"-r'A') + v + A. + 4 + ^L = 0. (103,3)}

-■~(2rr" + г'² - гг'К') + -р- {rf% + г² + 1) = 8nke, (103,4) 2г'-л.г' = 0, (103,5)

²) В этом параграфе полагаем с = 1.

³) Ср. задачу 5 § 100. Уравнения (103,2—5) получаются соответственно из уравнений (2) — (5) этой задачи, если положить в hhxv = 0, = г², р=> = 0. Заметим, что второе из уравнений (6) этой же задачи при р — 0 дает \' = 0, т. е. v = v(t); оставшийся в метрике (1) произвол в выборе т по- зволяет поэтому обратить v в нуль, чем снова демонстрируется возможность введения синхронно-сопутствующей системы отсчета.

где штрих означает дифференцирование по R, а точка — по т.

Уравнение (103,5) непосредственно интегрируется по вре­мени, давая

(103,6)

1 + f(R) *

где }(ЯУ—произвольная функция, удовлетворяющая лишь усло­вию 1+/>.0. Подставив это выражение в (103,2), получим

2rf + r²-/ = 0

(подстановка же в (103,3) не дает ничего нового). Первый инте­грал этого уравнения есть

fi^fW + lHL, (103,7)

где F(R)—еще одна произвольная функция. Отсюда

dr

Получающуюся в результате интегрирования зависимость r(x, R) можно представить в параметрическом виде:

r = |r(chT)-l), T₀(/?)-T = ^_r(shri-Ti)npH/>0, (103,8)

r = -^-(l — cosrj), т₀(R) - т = ₂ _^ ,_/t (л — sin г\) при / < 0,

(103,9)

где x₀(R)— снова произвольная функция. Если же / = 0, то

г = при /-0. (103,10)

Во всех случаях, подставив (103,6) в (103,4) и исключив f с по­мощью (103,7), получим следующее выражение для плотности материи'):

8л.£е = -£г. (103,11)

²) Из него выпадает, однако, особый случай, в котором г = г(т) и не зависит от R, так что уравнение (103,5) сводится к бессодержательному тождеству; см. В. А. Рубан, ЖЭТФ 56, 1914 (1969). Этот случай, однако, не соответствует условиям задачи о коллапсе конечного тела.

Формулы (103,6—11) определяют искомое общее решение²). Заметим, что оно зависит всего от двух «физически различных* произвольных функций: хотя в нем фигурируют три функции /,

F, то, но сама координата R может еще быть подвергнута про­извольному преобразованию R = R(R'). Это число как раз соответствует тому, что наиболее общее центрально-симметрич­ное распределение материи задается двумя функциями (распре­деление плотности и радиальной скорости материи), а свободного гравитационного поля с центральной симметрией вообще не су­ществует.

Поскольку система отсчета сопутствует материи, то каждой частице вещества отвечает определенное значение R; функция же r(x, R) при этом значении R определяет закон движения данной частицы, а производная г есть ее радиальная скорость. Важное свойство полученного решения состоит в том, что зада­ние входящих в него произвольных функций в интервале от 0 до некоторого R₀ полностью определяет поведение сферы этого радиуса; оно не зависит от того, каким образом заданы эти функции при R > Ro. Тем самым автоматически получается ре­шение внутренней задачи для любой конечной сферы. Полная масса шара дается, согласно (100,23), интегралом

г (Т, йо) &

^{т — 4л ^ zr2dr — 4я ^ e.r2r'dR.}

о о

Подставив сюда (103,11) и заметив, что F(0) = 0 (при R = 0 должно быть и /- = 0), найдем:

^m^^£W¹' ^rs=F(Xo) (Ю3,12)

(r_g— гравитационный радиус шара).

При i^? = const=^=0 из (103,11) имеем е = 0, так что решение относится к пустому пространству, т. е. описывает поле точеч­ной массы (находящейся в центре — особой точке метрики). Так, положив F = r_g, f = 0, xo = R, получим метрику (102,3)').

Формулы (103,8—10) описывают (в зависимости от пробегае­мой параметром т) области значений) как сжатие, так и расши­рение шара; то и другое в равной степени допускаются самими по себе уравнениями поля. Реальной задаче о поведении не­устойчивого массивного тела отвечает сжатие — гравитационный коллапс. Решения (103,8—10) выписаны таким образом, что сжатие имеет место, когда т, увеличиваясь, стремится к то- Мо­менту x=xo(R) отвечает достижение центра веществом с за­данной радиальной координатой R (при этом должно быть т₀>0).

') Случай же F — 0 (причем из (103,7): r = «Jf (^х ~ То)) соответствует отсутствию поля; надлежащим преобразованием переменных метрика может быть приведена к галилеевой.

Предельный характер метрики внутри шара при x-^to(R) одинаков во всех трех случаях (103,8—10):

г~(^)'^/9(т₀-т)Ч ^_ж(Е)^,А_^_._(То_г)-*. (Ю3,13)

Это значит, что все радиальные расстояния (в рассматриваемой сопутствующей системе отсчета) стремятся к бесконечности, а окружные — к нулю, причем все объемы тоже стремятся к нулю (как т — то)¹)- Соответственно этому плотность материи неограниченно возрастает ²):

8яЬ « Ж- г-. (103,14)

3F/₀(t₀-t)

Таким образом, в соответствии со сказанным в § 102, происхо­дит коллапс всего распределения материи в центр³).

В частном случае, когда функция To(#) = const (т. е. все частицы достигают центра одновременно), метрика внутри сжи­мающегося шара имеет другой характер. В этом случае

⁸"*⁸~3TSrW- ⁽¹⁰³'¹⁵⁾

т, е. при t-vto все расстояния — как окружные, так и ради­альные— стремятся к нулю по одинаковому закону ~(т₀— т)''>; плотность материи стремится к бесконечности как (то — т)~², причем в пределе ее распределение становится однородным.

') Геометрия на проходящей через центр «плоскости» при этом такая, которая была бы на конусообразной поверхности вращения, растягивающейся с течением времени по своим образующим и одновременно сжимающейся по всем своим окружностям.

²) Тот факт, что в рассматриваемом решении коллапс возникает при любой массе шара — естественное следствие пренебрежения давлением. Разумеется, при г -*■ °о предположение о пылевидности вещества с физиче­ской точки зрения во всяком случае непригодно, и следует пользоваться ультрарелятивистским уравнением состояния р --= е/3. Оказывается, однако, что общий характер предельных законов сжатия в значительной степени не зависит от уравнения состояния материи (см. Е. М. Лифшиц, И. М. Ха­латников, ЖЭТФ 39, 149 (I960)).

*) Случай т₀ = const включает в себя, в частности, и коллапс пол­ностью однородного шара — см. задачу.

Обратим внимание на то, что во всех случаях момент про­хождения поверхности коллапсирующего шара под шварцшиль-дову сферу (г(т, Ro) = r_g) ничем не замечателен для его внут­ренней динамики (описываемой метрикой в сопутствующей си­стеме отсчёта). В каждый момент времени, однако, определен­ная часть шара уже находится под своим «горизонтом событий».

Подобно тому, как F{R₀) определяет, согласно (193,12)', грави­тационный радиус шара в целом, так F(R) для любого задан­ного значения R есть гравитационный радиус части шара, рас­положенный под сферической поверхностью R = const; поэтому указанная часть шара определяется в каждый момент времени т условием г(т, /?)<; F(R).

Наконец, покажем, каким образом полученными формулами можно воспользоваться для решения поставленного в конце § 102 вопроса: построения наиболее полной системы отсчета для поля точечной массы ').

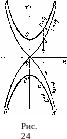Для достижения этой цели надо исходить из такой метрики в пустоте, которая содержала бы как сжимающуюся, так и рас­ширяющуюся пространственно-временные области. Таковым является решение (103,9), в котором надо положить F = const = r_s. Выбрав также

получим:

f — ioir и_l i • ^то⁼ "о" ^rg(—/)^-,'^г.

(103,16)

t-Кт⁺¹)⁽'-^cos*

■—= -(-Д-+1) (Я - Т) + Sin Л): ^r8 * V ^гг /

когда параметр т] пробегает значения от 2я до 0, время т (при заданном R) моно­тонно возрастает, а г возрастает от нуля, проходит через максимум и снова убывает до нуля.

На рис. 24 линии АСВ и А'С'В' отвечают точке г = 0 (им со­ответствуют значения параметра т) = 2я и г) = 0). Линии АО А' и ВОВ' отвечают шварцшильдовой сфере r — r_s. Между А'С'В' и А'ОВ' расположена пространственно-временная область, в ко­торой возможно лишь движение от центра, а между АСВ и АОВ —- область, в которой движение происходит лишь по на­правлению к центру.

') Такая система была впервые найдена Крускалом [М. Kruskal, 1960) в других переменных (см Phys. Rev. 119, 1743 (I960)). Приведенная ниже форма решения, в котором система отсчета синхронна, принадлежит И. Д. Новикову (1963),

Мировая линия частицы, покоящейся относительно данной системы отсчета, — вертикальная прямая (R = const). Она на­чинается от г = 0 (точка а), пересекает сферу Шварцшильда в точке Ь, достигает в момент т = 0 наибольшего удаления (r = r_g{R²/rg-_T- 1)), затем частица снова начинает падать к сфе­ре Шварцшильда, пересекает ее в точке с и вновь достигает г = 0 (точка d) в момент

Полученная система является полной: оба конца мировой линии всякой движущейся в поле частицы лежат либо на истин­ной особенности г = 0, либо уходят на бесконечность. Не полная же метрика (102,3) охватывает собой только область правее линии АО А' (или левее ВОВ'), а такая же «расширяющаяся» система отсчета — область справа от ВОВ' (или слева от АОА'). Что же касается шварцшильдовой системы отсчета с метрикой [(100,14), то она охватывает лишь область справа от BOA' (или слева от АО В'),

Задача

Найти решение внутренней задачи для гравитационного коллапса пы­левидной однородной сферы, вещество которой в начальный момент по­коится.

Решение. Положив

То = const, f = — sin²/?, F = 2во sin³/?,

получим

r = a₀ sin R (1 — cos t]), т — т₀ = a₀ (tj — sin т|) (1)

(радиальная координата R здесь безразмерна и пробегает значения от 0 до 2я), При этом плотность

^8я*^е—27Г"~ Я ⁽²⁾

4(1 - cost])³

и при заданном т не зависит от R, т. е. шар однороден. Метрику (103,1) с г из (1) можно представить в виде

ds² = dx² - а² (т) [dR² + sin² R (dQ² + sin² 6 dip⁸)], (3)

a = a₀ (1 — cos г]).

Обратим внимание на то, что она совпадает с решением Фридмана для метрики мира, полностью заполненного однородной пылевидной материей (§ 112), — вполне естественный результат, поскольку сфера, вырезанная из однородного распределения материи, обладает центральной симметрией¹).

Поставленному начальному условию можно удовлетворить решением (1) с определенным выбором постоянных Оо, То. Изменив здесь для удобства определение параметра (г)->-я — т]), представим решение в виде

' =4г ^s'"d (l+cosr|), т= , ^Г" ₀ (т| + sin л), (4)

2 sin Ro 2 sin Яо

') Метрика (3) отвечает пространству постоянной положительной кри­визны. Аналогичным образом, положив f=sh² R, F=2o₀sh³/?, получим реше­ние, отвечающее пространству постоянной отрицательной кривизны (§ ИЗ).

причем (согласно (103,12)) гравитационный радиус шара r_g = r₀sin²R₀, В начальный момент (т = 0, п = 0) вещество покоится (f = 0), а 2яг₀ = = 2ял(0, Ro)—начальная длина окружности шара, Падение всего вещества в центр происходит в момент т = nr_a/2 sin R₀.

Время t в системе отсчета удаленного наблюдателя (шварцшильдова система) связано с собственным временем на шаре т уравнением

^ ^rJ i_IfL

г

где под г надо понимать значение г(т,/?₀), отвечающее поверхности шара. Интегрирование этого уравнения приводит к следующему выражению t в функции того же параметра tj:

_t ctgtfo + tg-Э-

— = ln

^re ctg«₀-tg-^

(причем момент t = 0 отвечает моменту т = 0). Прохождению поверхности шара через шварцшильдову сферу (r(x,R₀)=r_e) отвечает значение пара­метра г), определяемое равенством

2 1 ^Гй ■ 2 _П

COS -jr = = sin² /?₀.

* /"о

При приближении к этому значению время t -*■ оо — в соответствии со ска­занным в § 102').