- •Содержание
- •Предисловие
- •Раздел 1 Понятие матрицы. Определитель матрицы.
- •Задачи для тренинга
- •Раздел 2
- •Задачи для тренинга
- •Раздел 3 Понятие собственного числа и собственного вектора
- •Задачи для тренинга
- •Раздел 4 Приведение кривой второго порядка к каноническому виду
- •Задачи для тренинга
- •Раздел 5 Приложения собственных векторов и собственных значений в планировании эксперимента
Задачи для тренинга
Найти решение системы методом Крамера и Гаусса:
2.1
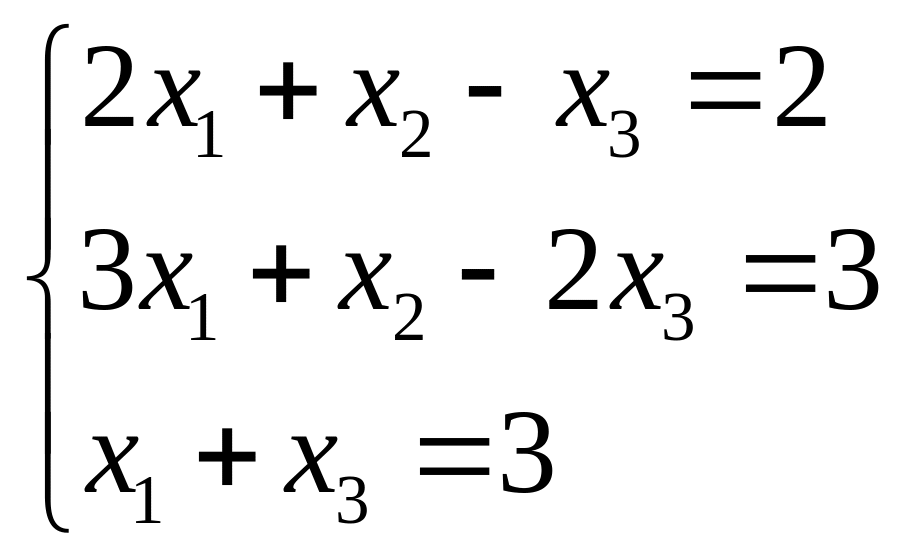 2.2
2.2
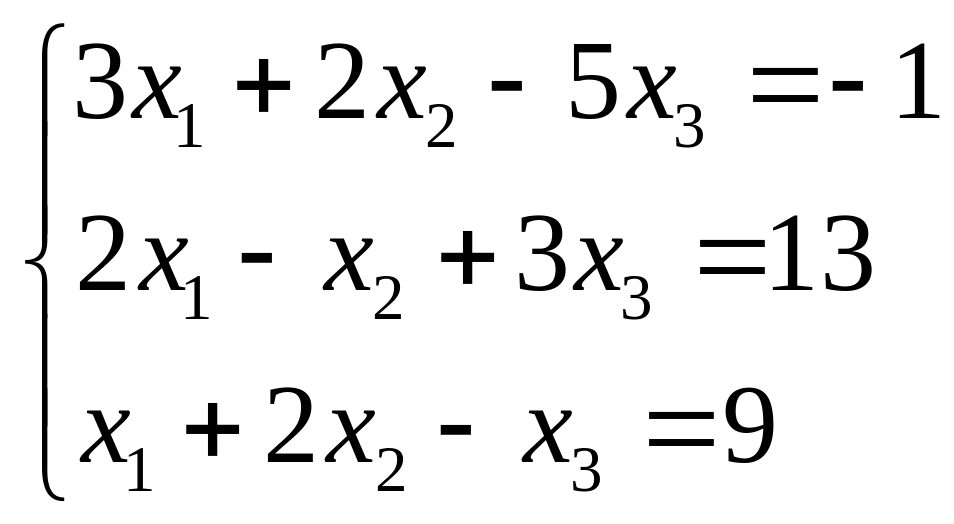 2.3
2.3
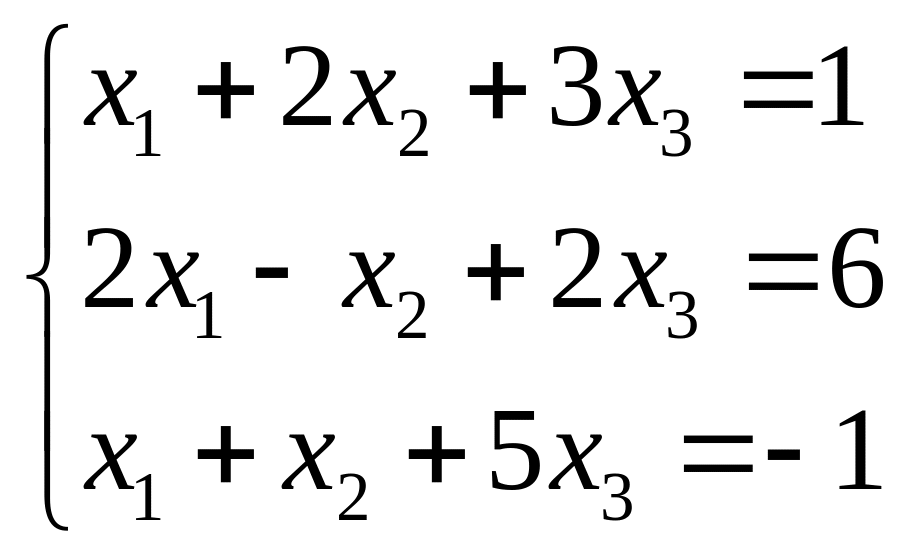
2.4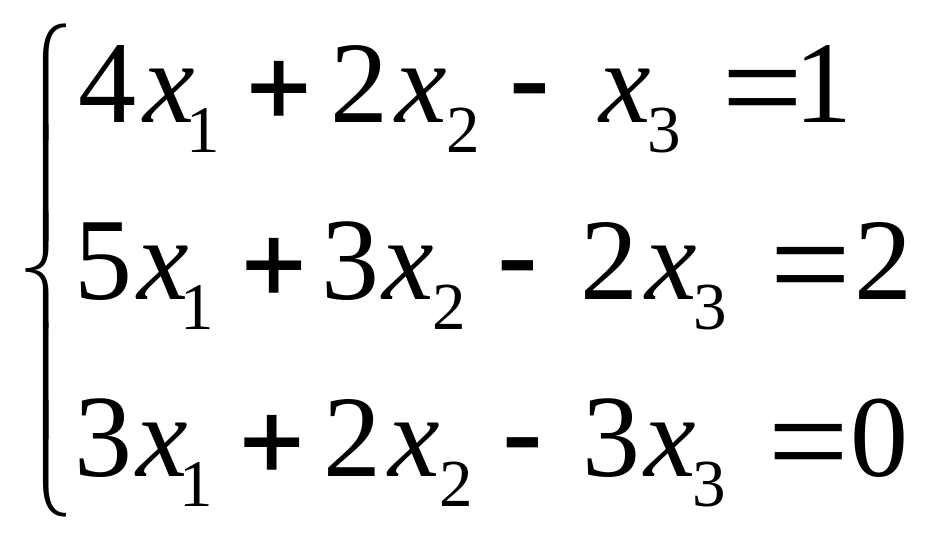 2.5
2.5
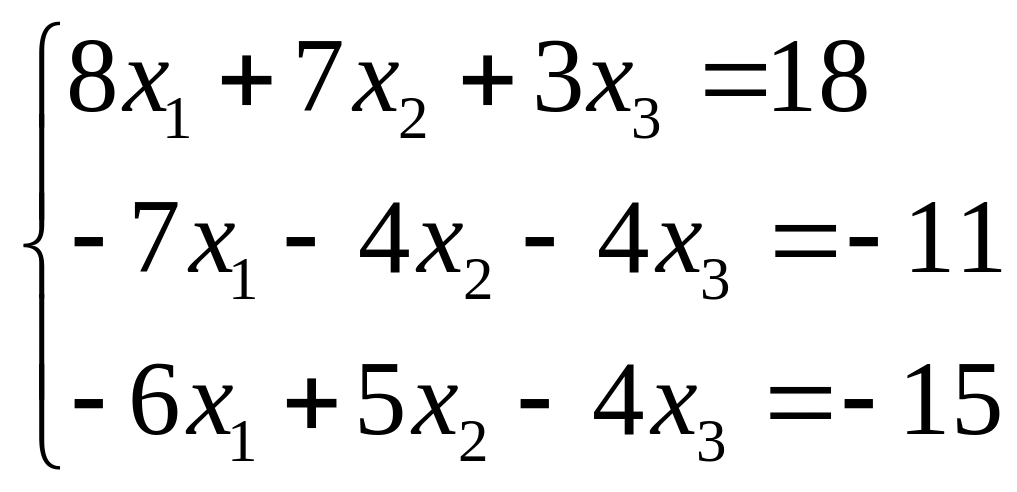
Раздел 3 Понятие собственного числа и собственного вектора
Собственное число
Собственный вектор
Определение 3.1. Число называется собственным числом (значением) квадратной матрицы A, если существует ненулевой столбец X такой, что
![]() .
.
Определение 3.2.
Если
собственное число матрицы A,
то всякий столбец X,
удовлетворяющий условиям
![]() ,
называется собственным столбцом
(вектором) матрицы
A, соответствующим
собственному числу .
,
называется собственным столбцом
(вектором) матрицы
A, соответствующим
собственному числу .
При условии, что
вектор
![]() ,
получаем характеристическое уравнение
для определения собственных значений
,
получаем характеристическое уравнение
для определения собственных значений
![]() .
(3.1)
.
(3.1)
Координаты
собственного вектора
![]() ,
соответствующие собственному значению
,
соответствующие собственному значению
![]() ,
являются решением системы уравнений
,
являются решением системы уравнений
![]() (3. 2)
(3. 2)
Определение собственных значений и собственных векторов матрицы
Схема |
Пример |
Определение собственных значений и собственных векторов матрицы |
|
|
Определить собственные значения и собственные векторы матрицы
|
1 |
Для
этого составим определитель матрицы
и от элементов, стоящих на главной
диагонали вычтем или
|
2 |
. Его
корнем, как легко проверить, будет
|
3. Определяем собственные вектора, соответствующие корням характеристичес-кого уравнения. |
Собственный
вектор
Или
Или как нетрудно заметить первое и третьи уравнения системы совпадают, значит, система может быть переписана в виде:
|
4. Выбираем базисные и свободные неизвестные и решаем полученную систему по одному из методов приденных в разделе 2. |
Пусть
Итак, система имеет решение
|
5. Необходимо придать одной неизвестной произвольные значение, получить решение исходной системы.
|
Придавая свободной
неизвестной
Следовательно,
первый собственный вектор
|
6. Для нахождения собственного вектора, соответствующего второму собственному значению,вновь составляется система по формуле (3.2) |
Второй собственный
вектор
Эта система сводится к системе
решение
которой
|
3. Третий вектор выписывается аналогичным образом. |
Третий собственный
вектор
Эта система
уравнений сводится к системе
|
Замечание. Если в процессе решения получилась несовместная система, то допущена ошибка (неверно вычислен характеристический многочлен, найденное не является собственным значением или допущена ошибка в вычислении коэффициентов системы линейных уравнений или в процессе решения системы).

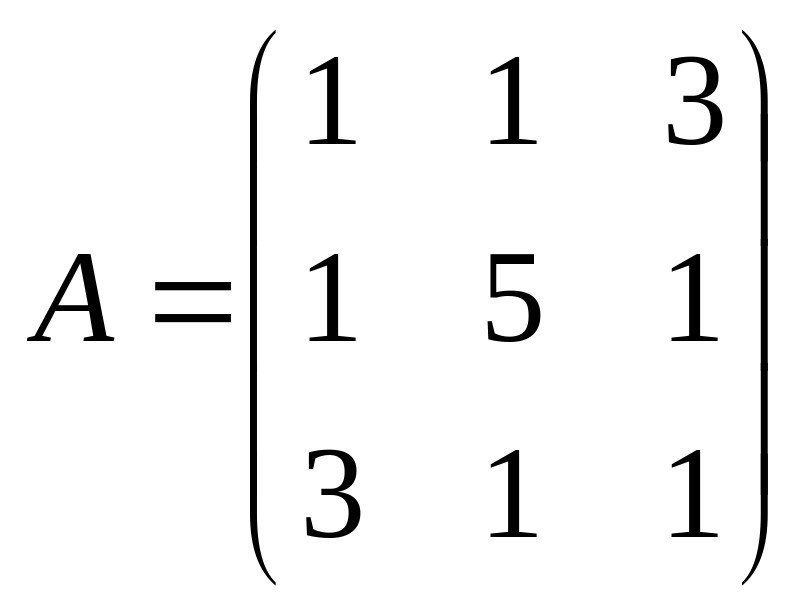 .
. .
Составляем характеристическое
уравнение для данной матрицы,
воспользовавшись формулой (3.1).
.
Составляем характеристическое
уравнение для данной матрицы,
воспользовавшись формулой (3.1).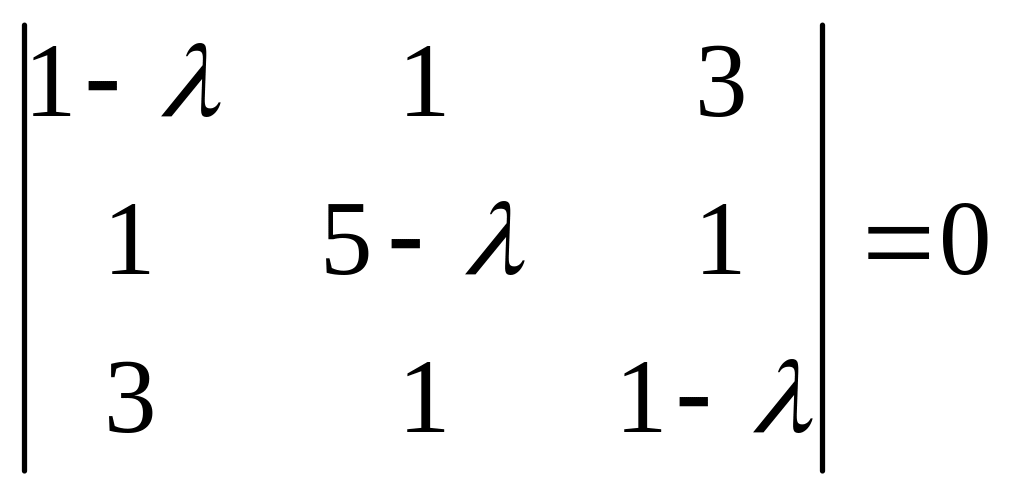
 .
Решаем полученное уравнение .
.
Решаем полученное уравнение .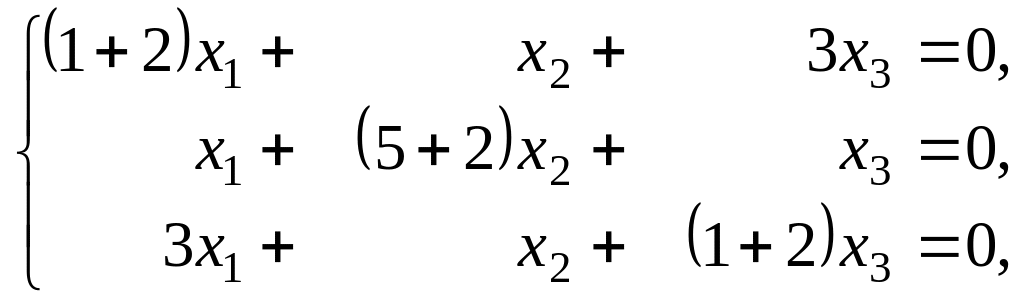
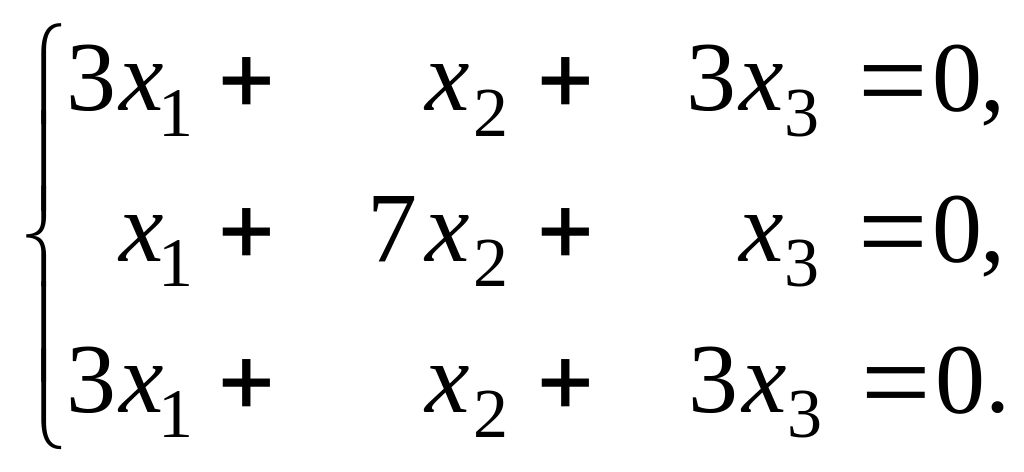
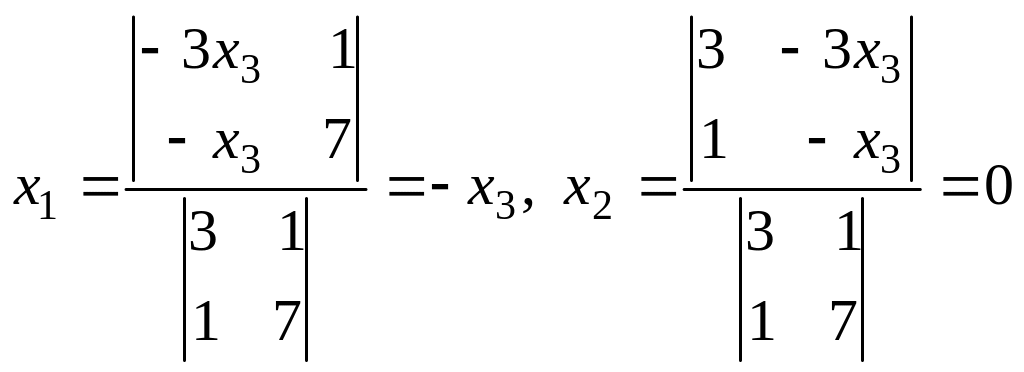 .
.