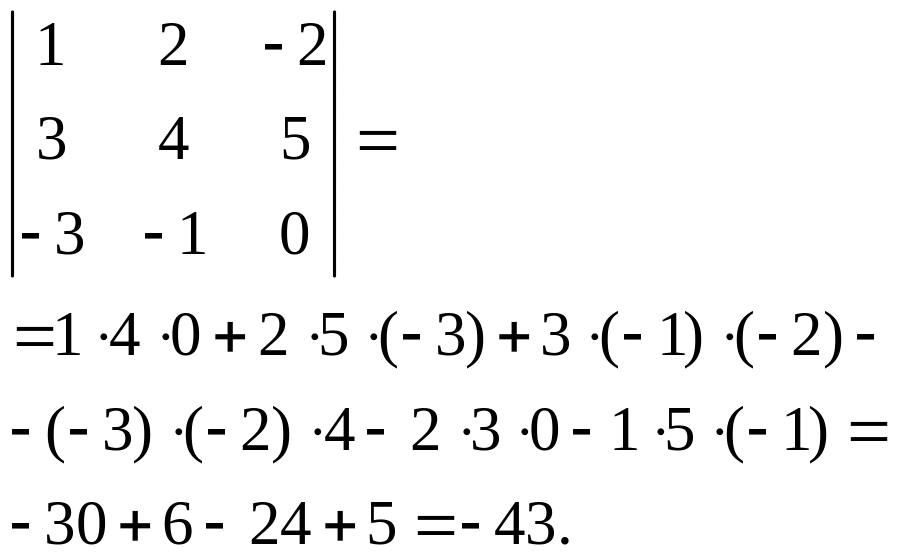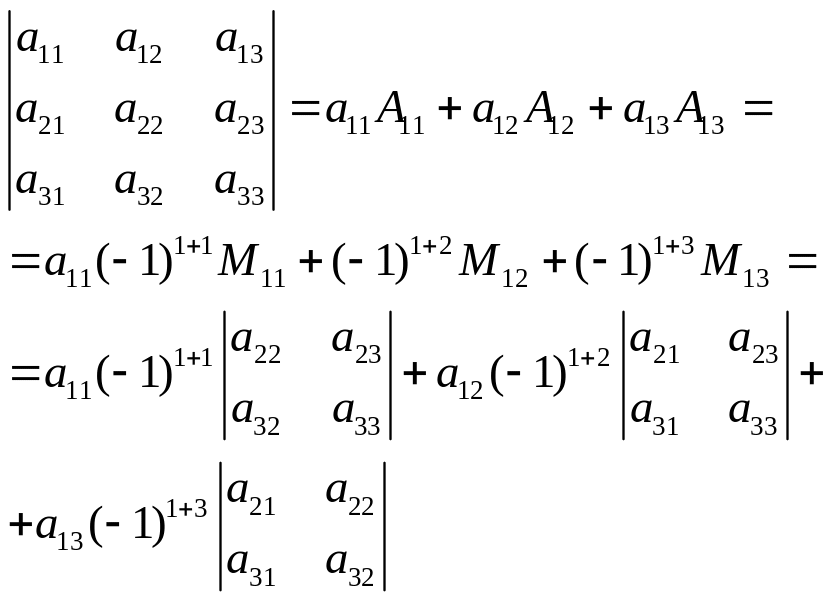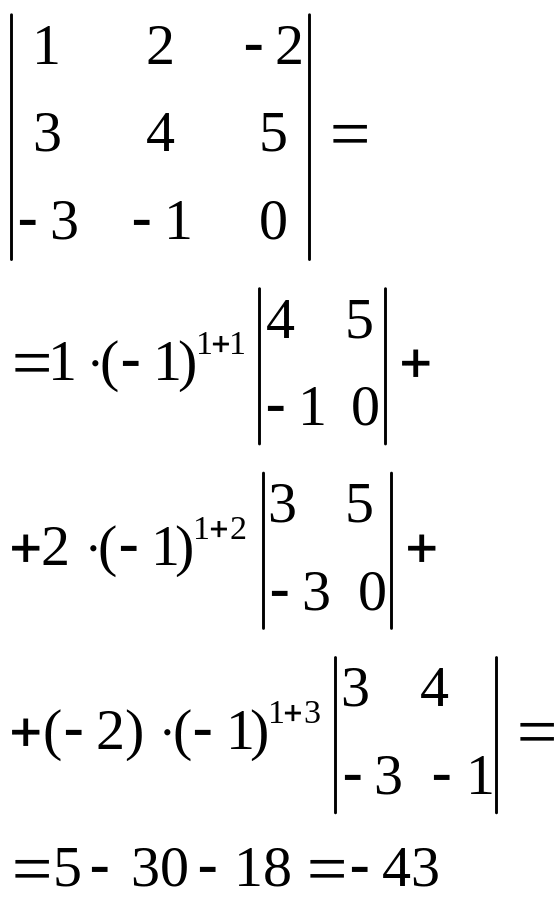19

Методические указания и задания

к изучению раздела курса прикладной математики

«Системы. Собственные числа и собственные вектора матрицы.»

(для студентов всех специальностей заочной и дневной форм обучения)

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

ДОНБАССКАЯ НАЦИОНАЛЬНАЯ АКАДЕМИЯ СТРОИТЕЛЬСТВА И АРХИТЕКТУРЫ

Методические указания и задания

к изучению раздела курса прикладной математики

«Системы. Собственные числа и собственные вектора матрицы.»

(для студентов всех специальностей заочной и дневной форм обучения)

Утверждено на заседании кафедры

Высшей и прикладной математики и

информатики

протокол № 9 от 17.04. 2013 г.

Макеевка 2013

УДК 512.64(07)

Методические указания и задания к изучению раздела курса прикладной математики

«Системы. Собственные числа и собственные вектора матрицы» (для студентов всех специальностей заочной и дневной форм обучения)/ Сост.: О.В. Александрова, Т.В. Жмыхова., Е.Ю. Чудина – Макеевка: ДонНАСА, 2013 г., - 19 с.

Содержат задачи по разделу курса прикладной математики «Системы. Собственные числа и собственные вектора матрицы» с примерами решений.

Составители: О.В, Александрова, доц.,

Т.В. Жмыхова, доц.,

К.Ю. Чудина, асс.

Рецензент: Ю.В. Грицук, к.т.н., доцент

Содержание

Предисловие……………………………………………………………………….5

Раздел 1. Понятие матрицы. Определитель матрицы…..............…..…….6

Задачи для тренинга........………………………………………………....…………………….8

Раздел 2. Понятие системы. Решение систем уравнений методом

Гаусса………………………………………………………………………………………….8

Задачи для тренинга...........……………………………………………....……………………11

Раздел 3. Понятие собственного числа и собственного вектора ….11

Задачи для тренинга...........……………………………………………....……………………14

Раздел 4. Приведение кривой второго порядка к каноническому виду...........……………………………………………....…………………………………….14

Задачи для тренинга...........….…………………………………………....……………………17

Раздел 5. Приложения собственных векторов и собственных значений в планировании эксперимента...........….……………………………17

Список использованной литературы…………………………………………18

Предисловие

Данное методическое пособие обеспечивает методическую поддержку раздела прикладной математики «Системы. Собственные значения и собственные вектора матриц» и может быть использовано для самостоятельного изучения этого раздела.

Каждый раздел пособия содержит логические части:

краткая теоретическая справка, в которой излагаются основные теоретические положения;

алгоритм решения задач с пошаговым описанием действий;

задачи для самостоятельного решения;

алгоритм решения задачи;

рекомендуемая литература.

При расчете строительных конструкций оценку величин критических нагрузок также проводят на основе информации о собственных значениях и собственных векторах матриц и поскольку математическое моделирование находит широкое приложение, то овладение методами решения проблемы определения собственных значений станет необходимым элементом инженерного образования.

Раздел 1 Понятие матрицы. Определитель матрицы.

• Матрица

• Определитель матрицы

Определение 1.1. Матрицей называется прямоугольная таблица, составленная из элементов некоторого множества. Записывается матрица в виде

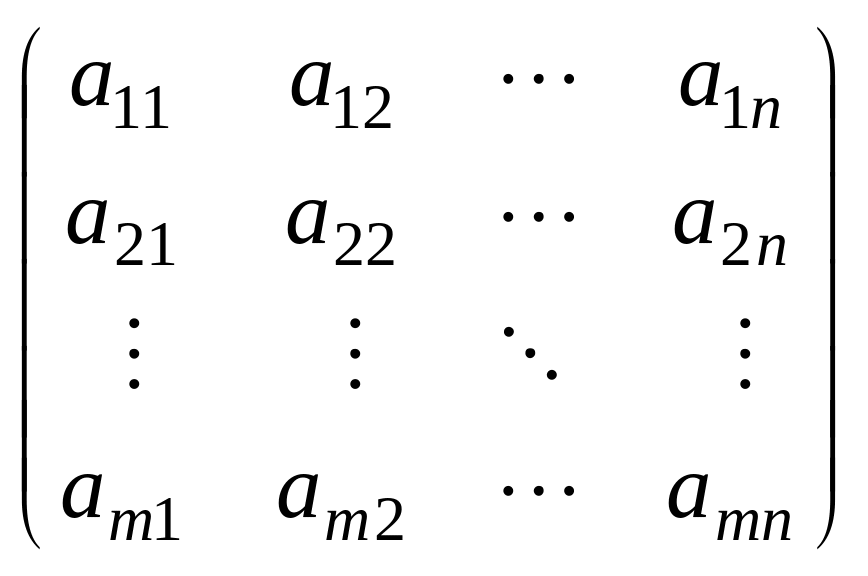. (1.1)

Здесь - элементы матрицы, нумеруемые двумя индексами. Индекс i элемента обозначает номер строки, индекс j – номер столбца, на пересечении которых находится этот элемент в матрице.

Определение 1.2. Матрица размера называется квадратной матрицей n-го порядка. Элементы образуют главную диагональ матрицы. Если у матрицы m строк и n столбцов, то, по определению, она имеет размерность .

Определение 1.3. Определитель, составленный из элементов квадратной матрицы, называется определителем матрицы и обозначается или .

Матрица E с элементами называется единичной матрицей n-го порядка.

Определение 1.4. Определителем (детерминантом) квадратной матрицы второго порядка называется число и обозначается:

(1.2)

Определение 1.5. Определителем квадратной матрицы третьего порядка 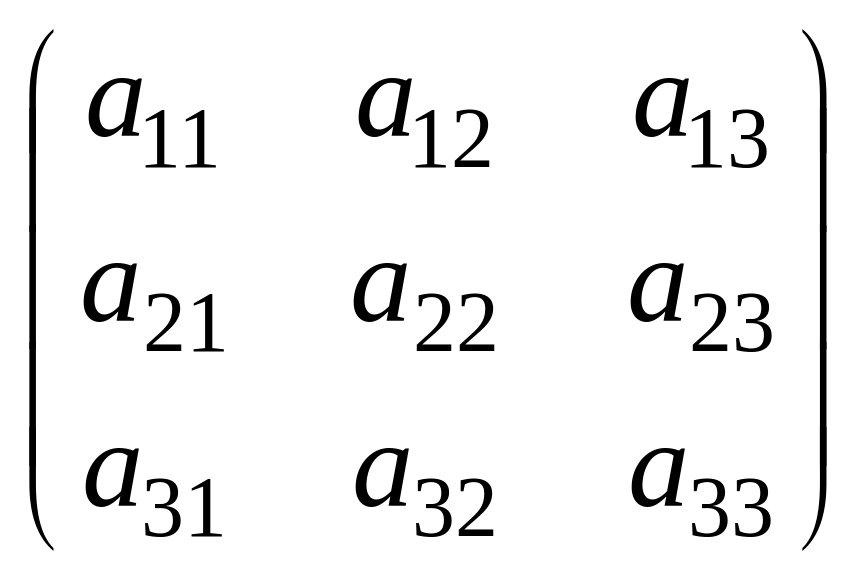называется число и обозначается:

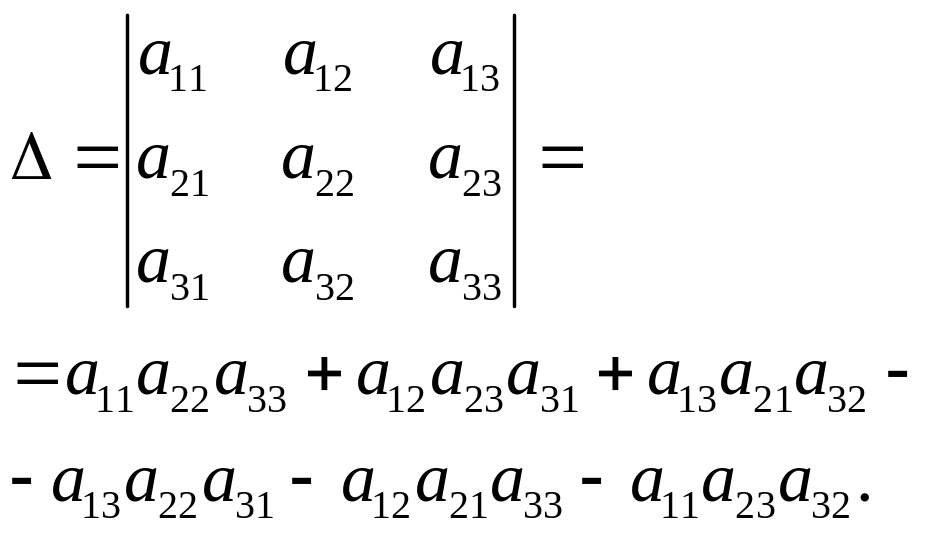(1.3)

Правила вычисления определителей:

Правило	Пример
Правила вычисления определителей матриц порядков 2 и более.
Схема вычисления определителя матрицы второго порядка:	Вычислить определитель . Решение:
Схема вычисления определителя матрицы третьего порядка (правило треугольника):	Вычислить определитель . Решение.
Схема вычисления определителя матрицы третьего порядка (разложение определителя по строке /столбцу): тут - минор элемента , - алгебраическое дополнение элемента .	Вычислить определитель . Решение.
Вычисление определителей выше третьего порядка производится путем использования различных свойств, которыми обладают определители.

Замечание. Определителем матрицы n-го порядка называется сумма всех произведений элементов этой матрицы, взятых по одному из каждой строки и по одному из каждого столбца; при этом каждое произведение снабжено знаком «плюс» или «минус» по некоторому правилу.
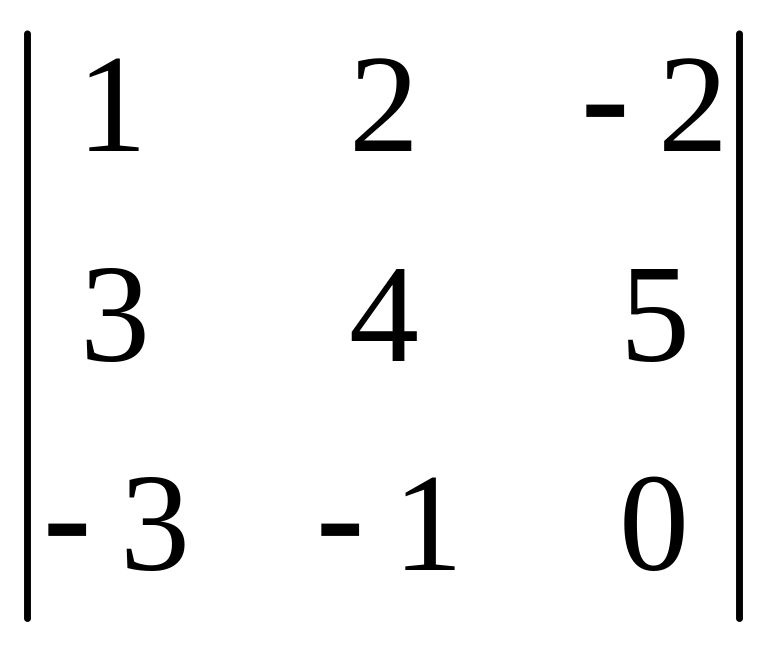