12. Випадкова величина х задана функцією щільності розподілу:
.
Якою формулою виражатиметься функція розподілу випадкової величини?
C)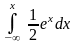 
;
13. З партії таблеток обсягом n = 40 знайдено середню массу m = 0,5 г таблетки та оцінки дисперсії 2,5∙10-5 г2. Значення середньо-квадратичного відхилення рівне:
E)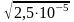 
.
14. При визначення рівня тиску в крові (мм. Водн.Ст.) в капілярах отримані дані: 16, 16, 15, 20, 20, 18, 35, 17, 19, 38. Чому дорівнює точкова оцінка середнього значення даних вимірювань?
A) 19,6;
15. Математичне сподівання випадкових величин M(X) = 4, а M(Y) = 1. Математичне сподівання M(X - Y) рівне:
C) 3;
1. Ряд розподілу випадкової величини це:
B) таблиця, в якій кожному значенню випадкової величини ставиться у відповідність її ймовірність;
2. Неперервна випадкова величина задається функцією: .
Функція щільності розподілу на проміжку 0 ≤ x ≤ 1 дорівнює:
D)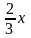 
;
3. Емпірична функція розподілу F(x) для дискретної випадкової величини визнача-ється як:
A) нагромадження
відносної частоти
;
4. Для контролю якості розчинів в ампулах для ін’єкцій із серії 8000 ампул вибрали 630. Яка із сукупностей є генеральною?
A) n = 8000;
5. Математичне сподівання для неперевної випадкової величини розраховують за формулою:
B) 
;
6. При дослідженні сироватки крові на холестерин (мг %) у n = 9 чоловіків (46-50 років) під час гіпертонічного кризу вибіркове середнє значення = 23%. Чи є дане вибіркове середнє оцінкою математичного сподівання?
B) так;
7. Яка випадкова величина є неперервною?
A) яка приймає будь-яке значення з інтервалу в якому вона існує;
8. Якому закону можуть підпорядковуватися неперервні випадкові величини?
C) нормальному закону;
9. Що таке точкове оцінювання хара-ктеристик розподілу досліджуваної ознаки?
A) визначення оптимальної оцінки статистичної характеристики;
10. Дисперсія неперервної випадкової величини дорівнює 3,5. Чому дорівнює середньоквадратичне відхилення:
A)
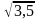
11. Заданий ряд розподілу незалежної випадкової величини y:
Y |
1 |
2 |
3 |
Py |
0,3 |
0,5 |
0,2 |
Математичне сподівання рівне:
A) 1, 9;
12. Дисперсія від
константи
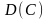рівна:
C) 0;
13. Вакцина формує імунітет від деякого захворювання з ймовірністю 0,999. Провакциновано 4000 мешканців міста. Якому середньому значенню відповідає число непровакцинованих?
D) 4;
14. Випадкова величина X задається функцією щільності розподілу:
.
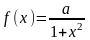Якою формулою виражатиметься функція розподілу?
D)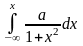 
;
15. Дисперсія неперервної випадкової вели-чини X дорівнює 9. Чому дорівнює середньо-квадратичне відхилення величини X?
D) 3;