
- •Елементи математичної статистики
- •5. Для якого варіаційного ряду графічно будують гістограму частот?
- •4. Протягом 20 тижнів число невиконаних замовлень фармацевтичною фірмою складає ряд: 12, 15, 18, 16, 12, 15, 18, 16, 14, 12, 14, 12, 16, 13, 13, 14, 16, 15, 4, 8. Як побудувати ряд розподілу?
- •12. Випадкова величина х задана функцією щільності розподілу:
- •14. При визначення рівня тиску в крові (мм. Водн.Ст.) в капілярах отримані дані: 16, 16, 15, 20, 20, 18, 35, 17, 19, 38. Чому дорівнює точкова оцінка середнього значення даних вимірювань?
- •2. Неперервна випадкова величина задається функцією: .
- •11. Заданий ряд розподілу незалежної випадкової величини y:
- •Поняття про диференціальні рівняння
- •Основи диференціального числення
- •2. Похідна функції рівна:
- •3. Перша похідна функції продукту хімічної реакції визначає:
- •Основи інтегрального числення
- •Елементи теорії ймовірності
- •7. Які події називають незалежними?
- •8. Які значення може приймати ймовірність випадкової події р(а):
- •1. Які події називаються залежними?
- •2. Події а і в незалежні і несумісні. Ймовірність появи однієї з цих двох подій визначається формулою:
- •3. Задані ймовірності , . Ймовірність дорівнює:
- •3. Яку подію називають неможливою?
- •4. Статистичне означення ймовірності випадкової події виражається так:
- •7. Якщо події а1, а2, ... Аn утворюють повну групу, то
- •10. Предметом вивчення теорії ймовірностей є:
- •8. Які події називаються протилежними?
- •11. Гральний кубик підкидають один раз. Яка ймовірність того, що випаде парне число?
- •15. Деяке захворювання, яке зустрічається у 5% населення, важко діагностувати. Яка ймовірність того, що пацієнт здоровий?
Елементи математичної статистики
1. Випадкові величини Х поділяються на:
E) дискретні і неперервні.
2. Сила стуму вимірюється амперметром класу точності 1,5. Отримані такі результати: 0,3; 0,28; 0,31; 0,31; 0,3; 0,29; 0,28; 0,32; 0,3 А. Істинне значення сили струму становить:
C) 0,3;
3. Дискретна випадкова величина має розподіл:
х |
-1 |
0 |
3 |
8 |
р |
0,2 |
0,3 |
0,3 |
0,2 |
Математичне сподівання М(х) = 2,3; дисперсія D(х) = 10,4. Яке середньо-квадратичне відхилення?
3,2;
4. Якщо випадкова величина задається біномним законом розподілу, то ця величина
B) дискретна;
C) інтервальна;
5. Функція розподілу
є неспадною при
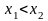 ,
то має місце нерівність:
,
то має місце нерівність:
C) 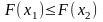 ;
;
6. Для яких числових характеристик задається точкова оцінка?
B) для математичного сподівання, дисперсії, середньоквадратичного відхилення;
.
7. Оцінку дисперсії для дискретної випадкової величини розраховують за формулою:
B) 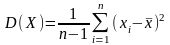 ;
;
8. Неперервна
випадкова величина задана функцією
розподілу:
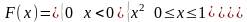 .
Чому дорівнює функція щільності
розподілу f(x)?
.
Чому дорівнює функція щільності
розподілу f(x)?
C) 2х;
9. Якщо випадкова
величина задається функцією щільності
розподілу:
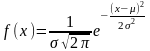 ,
то це:
,
то це:
B) неперервна випадкова величина;
10. Дисперсія дискретної випадкової величини дорівнює 1,7. Чому рівне середньо-квадратичне відхилення випадкової величини?
A)
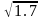
11. Заданий ряд розподілу незалежної випадкової величини Y:
Y |
1 |
2 |
3 |
Py |
0,3 |
0,5 |
0,2 |
Математичне сподівання рівне:
1,9;
12. Випадкова величина Х задана функцією щільності розподілу:
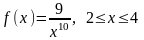 .
.
Якою формулою виражатиметься функція розподілу?
B)
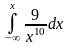 ,
x
є (-
,
x
є (-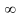 ;
);
;
);
13. Для розрахунку дисперсії неперервної випадкової величини використовують формулу:
A) 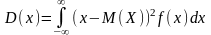
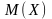 –
математичне
сподівання;
–
математичне
сподівання;
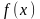 – функція щільності розподілу.
– функція щільності розподілу.
14. Вимірювання
об’єму ампул 1% розчину аскорбінової
кислоти в 40% розчині глюкози дало середнє
значення
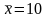 мл
з дисперсією
мл
з дисперсією
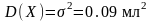 .
Чому дорівнює середньоквадратичне
відхилення?
.
Чому дорівнює середньоквадратичне
відхилення?
B) 0,3;
15. До якого типу випадкових величин можна віднести вагу і зріст людини?
C) неперервні;
1. Дано закон розподілу незалежної випадкової величини:
Х |
-5 |
2 |
3 |
4 |
Р |
0,4 |
0,3 |
0,1 |
0,2 |
Математичне сподівання випадкової величини дорівнює:
C) -0,3;
2.
Функція розподілу випадкової величини
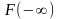 і
і
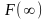 дорівнює:
дорівнює:
D) = 0; = 1;
3. Для яких випадкових величин має місце функція щільності розподілу?
B) неперервних;
4. Яка
із заданих формул дозволяє обчислити
ймовірність попадання випадкової
величини в заданий інтервал
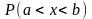 :
:
E) 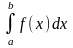 .
.
