Формулы равнопромежуточных нкп

,

₀

, , ,

m=1,

, ,

p=n, Рис.16

. Рис. 16

Рис.16

Сетка и эллипсы искажений данной проекции, изображены на рисунке 16.

3.6.Азимутальные проекции.

Нормальные азимутальные проекции (НАП).

а) б)

Рис.17

Геометрический смысл НАП показан на рисунке 17а. Картографическая сетка в этой проекции (рис. 17б) сходна с сеткой НКП: здесь параллели – концентрические окружности, а там – части концентрических окружностей; здесь меридианы – прямые, пересекающиеся в полюсе, а там – прямые, сходящиеся к полюсу. Поэтому НАП в теории проекций рассматривается как частный случай нормальных конических проекций, в которых параметр , поэтому их формулы выводятся аналогично формулам НКП с учетом данного условия. Поскольку в НАП искажения отсутствуют в точке полюса, то они применяются для картографирования полярных областей Арктики и Антарктики. Также как рассмотренные конические проекции НАП бывают равноугольные, равновеликие и равнопромежуточные с соответствующими для каждого вида формулами, сеткой и распределением искажений.

Перспективно-азимутальные проекции (пап).

Рис.18

В ПАП поверхность земного шара с радиусом R проецируется по закону линейной перспективы на плоскость К из точки зрения Т. Если точка зрения находится перед плоскостью (Т_п), то проекция образует позитивное изображение поверхности, а если за шаром (Т_н)- негативное изображение. Последний вид проекций подразделяется на подвиды в зависимости от расстояния (Д) от точки Т_н до центра шара, О: 1) Д=0 – гномонические; 2)Д=R –стереографические 3) R<Д<∞ - внешние;) Д=∞ -ортографические. Они показаны на рисунке 19 и обладают следующими свойствами.

1

) В гномонической ПАП ортодромии (геодезические линии) изображаются прямыми линиями, поэтому по сетке данной проекции легко определять промежуточные координаты ортодромий.

2

) В стереографической ПАП любая окружность изображается окружностью, поэтому ее применяют для карт звездного неба и графического решения по ним задач сферической астрономии.

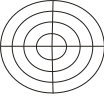3) Внешние ПАП подобны НАП и используются для карт северного и южного полушарий Земли или полушарий других планет.

4

) Ортографические ПАП хорошо передают сферичность, поэтому их применяют для картографирования планет и других шарообразных небесных тел.

Рис.19

7. Проекции и разграфки топографических карт и планов. Равноугольная поперечно-цилиндрическая (рпц) проекция Гаусса-Крюгера.

РПЦ проекция, геометрическая иллюстрация которой показана на рис. 20, применяется для отечественных топографических карт. В ней отображается поверхность меридианной зоны (координатной зоны) протяженностью 6⁰ или 3⁰ при следующих условиях: 1) средний меридиан отображаемой зоны принимается за осевой и является на плоскости осью абсцисс (Х) с сохранением длины дуги этого меридиана, а экватор – осью ординат (Y); 2) полюс используемой сферической системы координат располагается на географическом экваторе, ’_p=_э=0^о; 3) m=n сохраняются углы отображаемых фигур и направлений.

а) б) в)

Рис.20

Упрощенные формулы X и Y, а также формулы других величин проекции имеют вид:

,

,

,

m=n, p=m², =0, где , , , , S- длина дуги меридиана от экватора до текущей параллели; r – радиус текущей параллели; L₀ – долгота осевого меридиана зоны; N_K, N_З- номера меридианных колонки и зоны. Прямоугольные координаты и другие параметры картографической сетки РПЦ проекции определяются по книге «Таблицы координат …», в которой, кроме координат и параметров сетки, методики их определения, также изложена теория данной проекции.

РПЦ относится к проекциям двойного отображения - эллипсоида на шар, а шара на плоскость. Геометрически это выглядит следующим образом (рис. 20а,б):географическая сетка координатной зоны на эллипсоиде отображается сначала на шар (полярную сферическую систему координат с полюсом на географическом экваторе), а затем с поверхности шара на поверхность цилиндра (прямоугольную систему координат). Образуемая проекцией картографическая сетка схематически показана на рисунке 20в. Значения искажений длин и площадей (рис.20в), как следует из формул и рисунка проекции (рис.20б), зависят существенно от и незначительно от В: чем больше | | и меньше В, тем значения искажений больше и наоборот. На осевом меридиане искажения равны 0, а максимальные значения и находятся в точках пересечения крайних меридианов зоны с экватором ( , ).