Картография – отрасль научной и практической деятельности, которая занимается изучением, созданием и использованием различных видов карт и другой картографической продукции (планов, атласов, глобусов и т.д.).

Географическая карта – изображение информации об объектах Земли (геоинформации), построенное с применением картографической проекции, методов генерализации и графических обозначений. Объекты Земли – компоненты и комплексы географической оболочки и ее частей.

Картографическая проекция – уравнения, описывающие законы отображения поверхности земного эллипсоида или шара на плоскости.

Картографическая генерализация – обработка исходных планово-картографических материалов методами и приёмами обобщения и отбора информации для формирования содержания создаваемой карты.

Картографический знак – графический носитель информации об объектах Земли; имеет три составляющие: графическую, информационную и предметную.

План – изображение информации об объектах Земли, построенное в крупном масштабе (1: 5000 и крупнее), с применением ортогональной проекции, методов генерализации и графических обозначений.

Атлас – сборник взаимосвязанных географических карт.

Цифровая карта – цифровой аналог традиционной карты, представленный в виде структур геоданных в памяти компьютера или на внешнем носителе.

Картографическая проекция – математический закон отображения поверхности земного эллипсоида (или шара) на плоскости, который выражается системой уравнений, связывающих прямоугольные координаты с географическими. Общие формулы уравнений имеют вид:

,

.

Картографическая сетка – отображенная по формулам картографической проекции, построенная и графически изображенная на плоскости сетка географической системы координат.

Географическая система координат служит для определения положения точки на поверхности земного эллипсоида или шара значениями угловых величин широты и долготы. Широта определяется значением угла, заключенного между плоскостью экватора и направлением отвесной линии или нормали в данной точке. Долгота – это двугранный угол, заключенный между плоскостями, проходящими через начальный меридиан и меридиан данной точки. В случае использования при определении географических координат нормали координаты называются геодезическими и обозначаются B и L; а в случае применения отвесной линии они называются астрономическими и обозначаются  и . Параллель – линия, соединяющая точки одинаковых значений широты; меридиан – линия, соединяющая точки равных значений долготы. Сеть параллелей и меридианов (как правило, регулярная) на эллипсоиде или шаре называется сеткой географической системы координат или географической сеткой.

Масштабы: частный масштаб длин, μ – отношение бесконечно малого отрезка в любой точке карты к соответствующему бесконечно малому отрезку на поверхности эллипсоида и является функцией географических координат и азимута, ; главный масштаб или масштаб карты, - частный масштаб длин на главных элементах картографической сетки, например, на осевом меридиане в проекции равноугольной поперечно-цилиндрической (РПЦ) Гаусса-Крюгера; частный масштаб длин по меридиану - m; частный масштаб длин по параллели - n; масштаб площадей, p – отношение бесконечно малой трапеции в любой точке карты к соответствующей бесконечно малой трапеции на эллипсоиде, .

Искажения – это измеряемые отклонения в отображении проекцией длин, площадей и углов, которые определяются по формулам: искажения длин - , где за 1 принято значение μ₀; искажения площадей - , где 1=р_o, искажение углов - , где и - азимуты, соответственно на эллипсоиде и на карте.

Эллипс искажений – закон распределения значений в любой данной точке карты в зависимости от азимута ; закон описывается математически и изображается графически эллипсом (рис. 1); частным случаем эллипса, когда при комфорном отображении значений частного масштаба по всем направлениям равны, является окружность. Формула закона основана на понятии главных направлений. Главные направления – это два взаимно перпендикулярных направления на карте (X, Y), значения частного масштаба длин по которым являются экстремальными (по одному – максимальным, , а по другому – минимальным, ).В проекциях с ортогональными сетками и .

Х

У



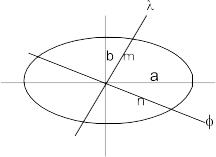
Рис.1

Изокола – линия, построенная на картографической сетке, соединяющая точки с равными значениями искажений , , ; изоколы, также как эллипсы искажений, применяются для изображения распределения значений искажений проекции на картах. Используются такие изображения при выборе проекций и для введения поправок в измеренные по картам значения длин, площадей и углов.

3.2.Классификации картографических проекций

Картографические проекции можно классифицировать по различным признакам, главными из которых являются: вид нормальной картографической сетки, характер (вид) искажений, положение полюса сферической системы координат.

На основании первого признака все КП подразделяются на цилиндрические, конические и азимутальные проекции и сходные с ними псевдоцилиндрические, псевдоконические и поликонические. Формулы цилиндрических проекций могут быть проиллюстрированы геометрически в виде цилиндра (рис. 7а), описывающего эллипсоид и касающегося его поверхности по линии экватора или по линиям двух близких к нему параллелей (рис. 8). Цилиндрические проекции образуют картографическую сетку

Р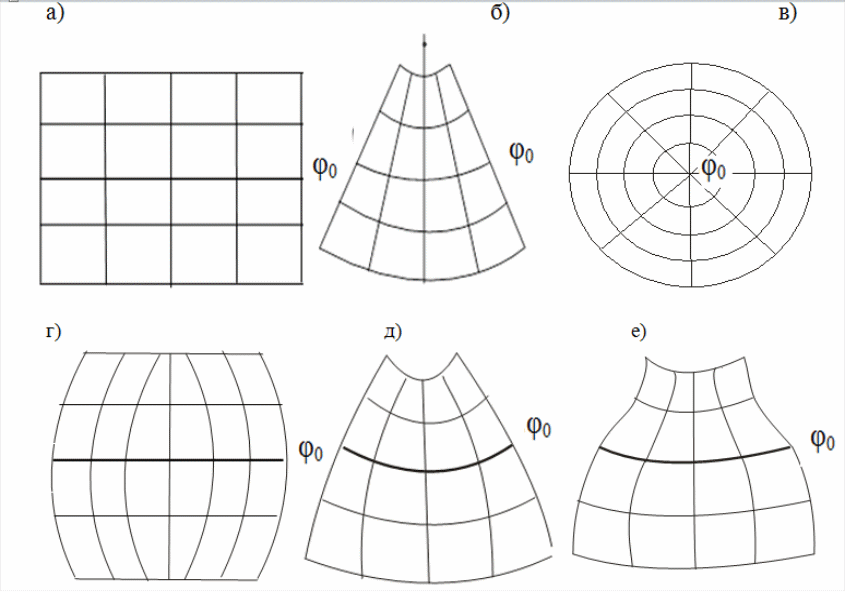 ис.2

прямоугольной формы (рис. 2а). В псевдоцилиндрических проекциях параллели совпадают с цилиндрическими, а меридианы – дуги, симметричные относительно среднего меридиана (рис. 2г).

Конические проекции иллюстрируются конусом, касающимся поверхности эллипсоида по линиям одной или двух параллелей (рис. 13а); образуют сетку, меридианы которой – прямые линии, сходящиеся к точке плюса, а параллели – дуги концентрических окружностей с центром в точке полюса (рис. 2б). В псевдоконических проекциях параллели совпадают с коническими, а меридианы являются дугами, симметричными относительно среднего меридиана (рис. 2д). В поликонических проекциях параллели - дуги разноцентровых окружностей, а меридианы – кривые, имеющие точку перегиба (рис. 2е). Азимутальные проекции иллюстрируются плоскостью, которая касается эллипсоида в точке полюса, и образуeт сетку, параллели которой - концентрические окружности, а меридианы – прямые, пересекающиеся в точке полюса (рис. 2в).

По характеру искажений различают равноугольные, равновеликие и равнопромежуточные проекции. Равноугольные проекции не искажают горизонтальные углы, но существенно искажают площади; главным условием получения этих проекций является равенство частных масштабов по всем направлениям, в том числе по параллелям и меридианам, .

Равновеликие проекции не искажают площади, но существенно искажают углы. Главное условие этих проекций - во всех точках карты p=1.

Равнопромежуточные проекции являются самым распространенным вариантом класса произвольных проекций; в них присутствуют все виды искажений, но их значения небольшие; главное условие этих проекций – m=1.

Картографическая проекция, которая непосредственно ( без использования вспомогательной сферической системы координат) отображает сетку географической системы координат, и образуемая ею картографическая сетка называются нормальными; в нормальных проекциях географическая и используемая полярная сферическая системы и соответственно их полюсы совпадают ( ).

Картографическая проекция, в которой используется полярная сферическая система координат с полюсом, расположенным относительно географической системы координат на ее экваторе ( ), называется поперечной. Картографическая проекция, в которой используется полярная сферическая система с полюсом, расположенным между географическим полюсом и экватором ( ), называется косой. Пример полярной сферической системы, используемой в поперечных и косых проекциях, изображен на рисунке 3. Положение точки А в системе определяется азимутом, который равен двугранному углу между плоскостями начального вертикала и вертикала, проходящего через точку А, а также зенитным расстоянием Z , равным длине дуги вертикала от полюса p` до точки А. Малые круги, ерпендикулярные к вертикалам, называются альмукантаратами.

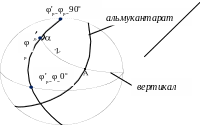
Рис.3.