11. Проверка гипотезы о соответствии наблюдаемых значений равномерному распределению.

Для того, чтобы при уровне значимости α, проверить гипотезу о равномерном распределении выборочной совокупности 2, надо [2]:

1. Оценить параметры а и b – концов интервала, в котором наблюдались возможные значения случайной величины X, по формулам (28) и (29).

2. Найти плотность вероятности предполагаемого равномерного распределения по формуле (9).

3. Определить теоретические частоты по формулам:

;  ;

(32)

4. Найти наблюдаемое значение критерия Пирсона по формуле (30).

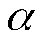5. Найти критическую точку (;r) по заданному уровню значимости а и числу степеней свободыr. Критическую точку(;r) находят по таблице критических точек распределения (приложение 4)

6. Принять или не принять гипотезу о равномерном распределении выборочной совокупности 2.

12. Построение доверительного интервала для генеральной средней и генеральной доли по большим выборкам.

Для построения доверительных интервалов для параметров генеральных совокупностей могут быть реализованы два подхода, основанных на знании точного (при данном объеме выборки п) или асимптотического(при п -> оо) распределения выборочных характеристик (или некоторых функций от них). Первый подход реализован далее при построении интервальных оценок параметров для малых выборок. В данном параграфе рассматривается второй подход, применимый для больших выборок (порядка сотен наблюдений).

Теорема. Вероятность того, что отклонение выборочной средней (или доли) от генеральной средней (или доли) не превзойдет число  (по абсолютной величине), равна:

_{, где  (23)}

_{, где  (24)}

 _{- функция (интеграл вероятности) Лапласса}

Выше (§ 9.4) показано, что выборочная средняя  и выборочная доля  повторной выборки представляют сумму n независимых случайных величин _{, где}  имеет один и тот же закон распределения — соответственно (13) и (10) с конечными математическим ожиданием и дисперсией. Следовательно, на основании теоремы Ляпунова при  распределения  и  неограниченно приближаются к нормальным (практически при  распределения  и  можно считать приближенно нормальными).

Для бесповторной выборки  и  представляют сумму зависимых случайных величин. Однакоможно показать, что и в этом случае при  закон распределения  и  как угодно близко приближается к нормальному.

Формулы (23) и (24) следуют непосредственно из свойства 2 нормального закона формулы.

Формулы (23) и (24) получили название формул доверительной вероятности для средней и доли.

Определение. Среднее квадратическое отклонение выборочной средней и выборочной доли собственно-случайной выборки называется средней квадратической (стандартной) ошибкой выборки. (Для бесповторной выборки обозначаем соответствено  и ).

Из рассмотренной теоремы вытекают следующие следствия.

Следствие 1. При заданной доверительной вероятности  предельная ошибка выборки равна (-кратной величине средней квадра-тической ошибки, где, т.е.

13. Сравнение двух средних нормальных генеральных совокупностей с неизвестными дисперсиями (зависимые выборки).

десь рассматриваются выборки одинакового объема, варианты которых попарно зависимы. Например, если х_i (i=1,2, ...,n)—результаты измерений деталей первым прибором, а y_i — результаты измерений этих же деталей, произведенные в том же порядке вторым прибором, то х_i и y_i попарно зависимы и в этом смысле сами выборки зависимые. Поскольку, как правило, х_i ≠ у_i, то возникает необходимость установить, значимо или незначимо различаются пары этих чисел. Аналогичная задача ставится при сравнении двух методов исследования, осуществленных одной лабораторией, или если исследование произведено одним и тем же методом двумя различными лабораториями.

Итак, пусть генеральные совокупности Х и Y распределены нормально, причем их дисперсии неизвестны. Требуется при уровне значимости α проверить нулевую гипотезу Н₀:М () = М () о равенстве генеральных средних нормальных совокупностей с неизвестными дисперсиями при конкурирующей гипотезе Н₁:М () ≠ М () по двум зависимым выборкам одинакового объема.

Сведем эту задачу сравнения двух средних к задаче сравнения одной выборочной средней с гипотетическим значением генеральной средней, решенной в § 13, п. Б. С этой целью введем в рассмотренные случайные величины—разности D_i = Х_i—Y_i и их среднюю

.

Если нулевая гипотеза справедлива, т.е. М () = М (),то М () - М () = 0 и, следовательно,

М () == М (—) = М () — М () = 0.

Таким образом, нулевую гипотезу Н₀:М () = М () можно записать так:

H₀:М() = 0.

Тогда конкурирующая гипотеза примет вид Н₁:М() ≠ 0.

Замечание 1. Далее наблюдаемые неслучайные разности x_i—y_i будем обозначать через d_i в отличие от случайных разностей D_i = Х_i—Y_i. Аналогично выборочную среднюю этих разностей обозначим черезв отличие от случайной величины.

Итак, задача сравнения двух средних  и сведена к задаче сравнения одной выборочной среднейс гипотетическим значением генеральной среднейМ() = а₀ = 0. Эта задача решена ранее в§ 13, п. Б, поэтому приведем лишь правило проверки нулевой гипотезы и иллюстрирующий пример.

Замечание 2. Как следует из изложенного выше, в формуле (см. § 13. п. Б)

надо положить

.

Тогда .

Правило. Для того чтобы при заданном уровне значимости α проверить нулевую гипотезу Н₀:М() = M() о равенстве двух средних нормальных совокупностей с неизвестными дисперсиями (в случае зависимых выборок одинакового объема) при конкурирующей гипотезе М() ≠ M(), надо вычислить наблюдаемое значение критерия:

и по таблице критических точек распределения Стьюдента, по заданному уровню значимости α, помещенному в верхней строке таблицы, и по числу степеней свободы k = п - 1 найти критическую точку t_{двууст.кр} (α; k).

Если |T_иабл|< t_{двууст.кр} — нет оснований отвергнуть нулевую гипотезу.

Если |T_иабл|> t_{двууст.кр} — нулевую гипотезу отвергают.