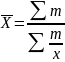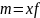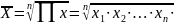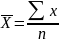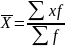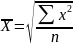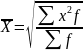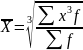Закон распределения случайной величины

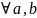Законом распределения случайной величины Х называется любая функция (правило, таблица и т.п.), устанавливающая соответствие между значениями случайной величины и вероятностями их наступления и позволяющая находить вероятности всевозможных событий p{a≤X b}, связанных со случайной величиной.

Для практической деятельности важно уметь сравнивать события по степени возможности их наступления. Например, интуитивно ясно, что при последовательном извлечении из колоды пяти карт более возможна ситуация, когда появились карты разных мастей, чем появление пяти карт одной масти; при десяти бросках монеты более возможно чередование гербов и цифр, нежели выпадение подряд десяти гербов, и т.д. Поэтому для сравнения событий нужна определенная мера.

Вероятность

Численная мера степени объективной возможности наступления события называется вероятностью события и является, наряду с понятием случайного события, вторым основным понятием теории вероятностей. Это определение, качественно отражающее понятие вероятности события, не является математическим. Чтобы оно таковым стало, необходимо определить его количественно.

Виды средних

Средняя величина — это обобщающий показатель, характеризующий типический уровень явления в конкретных условиях места и времени. Он выражает уровень признака, типический для каждой единицы совокупности.

Средние широко применяются в различных плановых, прогнозных, финансовых расчетах.

Главное значение средних величин состоит в их обобщающей функции, т.е. замене множества различных индивидуальных значений признака средней величиной, характеризующей всю совокупность явлений. Всем известны особенности развития современных людей, проявляющиеся в том числе и в более высоком росте сыновей по сравнению с отцами, дочерей в сравнении с матерями в том же возрасте. Но как измерить это явление?

В разных семьях наблюдаются самые различные соотношения роста старшего и младшего поколения. Далеко не всякий сын выше отца и не каждая дочь выше матери. Но если измерить средний рост многих тысяч лиц, то по среднему росту сыновей и отцов, дочерей и матерей можно точно установить и сам факт акселерации, и типичную среднюю величину увеличения роста за одно поколение.

На производство одного и того же количества товара определенного вида и качества разные производители (заводы, фирмы) затрачивают неодинаковое количество труда и материальных ресурсов. Но рынок осредняет эти затраты, и стоимость товара определяется средним расходом ресурсов на производство.

Все средние величины делятся на два больших класса:

• степенные средние; к ним относятся такие известные и часто применяемые виды, как средняя арифметическая величина, средняя квадратическая и средняя геометрическая;

• структурные средние величины, в качестве которых рассматриваются мода и медиана.

Степенные средние величины исчисляются в двух формах — простой и взвешенной.

Простая средняя величина считается по несгруппированным данным и имеет следующие общий вид:

где X_i – варианта (значение) осредняемого признака;

m – показатель степени средней;

n – число вариант (наблюдений).

Взвешенная средняя величина считается по сгруппированным данным, представленным в виде дискретных или интервальных рядов распределения:

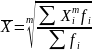
где X_i – варианта (значение) осредняемого признака или серединное значение интервала, в котором измеряется варианта;

m – показатель степени средней;

f_i – частота, показывающая, сколько раз встречается i-e значение осредняемого признака.

Приведем в качестве примера расчет среднего возраста студентов в группе из 20 человек.

№	Возраст (лет)	№	Возраст (лет)	№	Возраст (лет)	№	Возраст (лет)
1	18	6	20	11	22	16	21
2	18	7	19	12	19	17	19
3	19	8	19	13	19	18	19
4	20	9	19	14	20	19	19
5	19	10	20	15	20	20	19

Средний возраст рассчитаем по формуле простой средней:

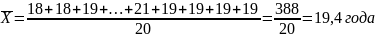
Сгруппируем исходные данные. Получим следующий ряд распределения:

Возраст, Х (лет)	18	19	20	21	22
Число студентов	2	11	5	1	1

В результате группировки получаем новый показатель — частоту, указывающую число студентов в возрасте X лет. Следовательно, средний возраст студентов группы будет рассчитываться по формуле взвешенной средней:

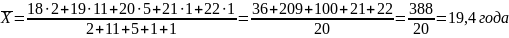
Общие формулы расчета степенных средних имеют показатель степени (m). В зависимости от того, какое значение он принимает, различают следующие виды степенных средних:

средняя гармоническая, если m = - 1;

средняя геометрическая, если m → 0;

средняя арифметическая, если m = 1;

средняя квадратическая, если m = 2;

средняя кубическая, если m = 3.

Если рассчитать все виды средних для одних и тех же исходных данных, то значения их окажутся неодинаковыми. Здесь действует правило мажорантности: с увеличением показателя степени т увеличивается и соответствующая средняя величина:

Xгарм ≤ Xгеом ≤ Xарифм ≤ Xквадр ≤ Xкуб.

Пользуясь этим правилом, статистика может в зависимости от настроения и желания ее "знатока" либо "утопить", либо "выручить" студента, получившего на сессии оценки 2 и 5. Каков его средний балл?

Если судить по средней арифметической, то средний балл равен 3,5. Но если декан желает "утопить" несчастного и вычислит среднюю гармоническую:

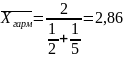
то студент остается и в среднем двоечником, не дотянувшим до тройки. Однако студенческий комитет может возразить декану и представить среднюю кубическую величину:

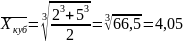
Студент уже выглядит "хорошистом" и даже претендует на стипендию! И только в том случае, если лентяй провалил оба экзамена, статистика помочь не в состоянии: увы, все средние из двух двоек равны все той же двойке!

Формулы степенных средних величин приведены таблице.

В формулах средних значений n — это число единиц совокупности (число индивидуальных значений осредняемого признака X); x — индивидуальное значение признака у каждой единицы. Если совокупность объектов распределена по группам разной численности, то x — это значение признака, общее для всей группы; f — численность группы (частота повторения данного значения признака).

Вид степенной средней	Показатель степени(m)	Формулы расчета средней
		Простой	Взвешенной
Гармоническая	-1
Геометрическая	→0
Арифметическая	1
Квадратическая	2
Кубическая	3