2.6. Предельные теоремы в схеме Бернулли.

Часто в лингвистических исследованиях приходится проводить большое число независимых испытаний n. При этом величина n может быть велика, что делает вычисление по формуле Бернулли слишком трудоёмким. В таких случаях применяют асимптотические формулы для вычисления биномиальной вероятности при n→∞.

1. Формула Пуассона , где параметр .

Формула применяется при большом количестве испытаний n (n≥100) и малой вероятности события А р (p≤0,1). При этом а≤10.

Если количество испытаний n велико, а вероятность р не близка к нулю, то для нахождения вероятности используются теоремы Муавра - Лапласа .

2. Локальная теорема Муавра-Лапласа

,

применяется при больших n и р≠0; р≠1.

Выражение называется функцией Гаусса, значения которой можно найти в таблице (табулированы).

При равенство дает удовлетворительное приближение.

3. Интегральная теорема Муавра-Лапласа

,

где - функция Лапласа, значения которой табулированы,

Теорема применяется в тех случаях, когда требуется вычислить вероятность, что в n независимых испытаниях событие А появится от до раз включительно, при больших n и р≠0; р≠1 ( ).

Примеры.

1) Вероятность появления числительного в художественной речи равна 0, 01 [Головин, 1971, с.123]. Исследуется текст, длиной 500 знаменательных слов. Найти вероятность, что в данном тексте окажется… а) 3 числительных; б) более 3 числительных.

Решение: a) так как вероятность появления каждого числительного мала, а число слов (количество испытаний) велико, то применим формулу Пуассона. Здесь n=500, p=0,01, a=500 0,01=5; m=3; 0,14.

б) обозначим событие А – «в тексте более 3 числительных», тогда событие – «в тексте не более 3 (т.е 0, 1, 2 или 3) числительных».

2) Вероятность появления существительного в русской художественной речи равна 0,40 [Головин, 1971, с.123]. Исследуется текст, длиной 200 знаменательных слов. Найти вероятность, что в данном тексте окажется а) 70 существительных; б) от 70 до 90 существительных.

Решение: так как n – велико (n=200), а вероятность р не близка к нулю (p=0,4; q=1-p=0,6), то для нахождения искомых вероятностей используется теоремы Муавра – Лапласа: локальная и интегральная.

а) .

Значение функции Гаусса при х=-1,44 равно 0,14 ;

б) . Φ(2,89)=0,498; Φ(1,44)=0,425; 0,073.

Лекция 3. Случайная величина

Случайное лингвистическое событие – результат лингвистического испытания и является качественной его характеристикой. Количественная характеристика результата опыта есть случайная величина. Например, случайная величина «число букв в слове» может принимать значения 1; 2; 3;…, а случайная величина «число гласных букв в слове» может принимать значения 1; 2; 3; …; 11. Появление одного из значений случайной величины – это случайное событие, появление всех значений случайной величины – совокупность случайных событий, образующих полную группу. Сумма вероятностей всех этих событий равна единице.

3.1. Начальные понятия

1) Случайная величина (СВ )– величина, которая может принимать определённые числовые значения в зависимости от исхода опыта. Обозначается заглавной буквой латинского алфавита. Например, СВ Х= «число сложноподчинённых предложений в тексте объёмом 500 словоформ».

2) Дискретная случайная величина (ДСВ) может принимать только отделённые друг от друга значения. Число значений дискретной случайной величины конечно или счётно.

Например, ДСВ Y = «количество глаголов в отрывке текста «Евгений Онегин», длиной 500 словоупотреблений».

3) Непрерывная случайная величина (НСВ) может принимать все значения из некоторого числового промежутка.

Например, HСВ Z= «высота звука человеческой речи»;

V = «интенсивность звука человеческой речи».

4) Случайная лингвистическая величина: длина слова, количество гласных и согласных фонем, число словоупотреблений в предложении и т.д. Когда фонолог, лексиколог или грамматист исследует структуру планов содержания или выражения, то он всегда имеет дело с дискретными СВ. Обращаясь к фонетическим или семантическим исследованиям лингвист должен оперировать непрерывными СВ.

5) Семантическая интерпретация непрерывной СВ

Между некоторыми родственными универсальными значениями нет чётких границ, и между ними всегда можно найти бесконечное число переходных смысловых оттенков. Особенно наглядно эта ситуация прослеживается в непрерывности цветового спектра. В каждом языке можно найти средства для обозначения тонких и ещё более тонких оттенков цветов, т.е. семантические интервалы цветового спектра сужаются. Если считать непрерывной СВ некоторое цветовое значение, то окажется, что СВ обязательно примет одно из своих возможных значений при извлечении предложения из соответствующего текста, хотя при многократном повторении опыта это значение будет появляться очень редко [Пиотровский, 1977, с.144].

6) Закон распределения СВ – правило, связывающее значения СВ и соответствующие им вероятности. Для ДСВ закон распределения можно представить в виде таблицы:

Х			…
P			…

где

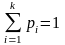
p_i

7) Многоугольник распределения –

л оманая линия, последовательно х_i

соединяющая точки с координатами