Определения вероятности событий

Сами события, которые могут произойти в данном испытании, вызывают ограниченный интерес. Гораздо важнее определить степень уверенности, что событие произойдёт. Для этого используется вероятность события. В обыденной жизни под вероятностью некоторого события понимают меру возможности появления этого события. Например, интуитивно мы можем сказать, что возможность появления буквы к в русских текстах больше, чем буквы ц, так как по нашим наблюдениям буква к появляется чаще. Это интуитивная вероятность. В теории вероятностей установлена чёткая процедура нахождения вероятности события. Существует несколько определений вероятности. В языкознании интерес представляет классическое и статистическое определение вероятности.

Классическое определение вероятности

1) Пусть в некотором опыте может произойти n равновозможных, несовместных событий (исходов), причём одно из них обязательно наступит.

2) Интересующее нас событие А наступит, если наступит одно из m (m ≤ n) равновозможных, несовместных, событий.

Тогда вероятность события А равна 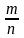, что записывается в виде 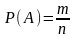- формула классической вероятности события А,

m – число событий , благоприятных событию А (из n),

n – число всего возможных исходов: равновозможных, несовместных, событий.

Свойства вероятности:

Исходя из классического определения вероятности, осуществляется, например, вероятностная обработка частотных словарей отдельных произведений или всего творчества писателя. В этих случаях все словоупотребления, составляющие текст, образуют полную группу равновозможных элементарных событий.

Пример. Текст «Капитанской дочки» А.С.Пушкина состоит из 29343 словоупотреблений. Формы слова «быть» встречаются здесь 430 раз. Найти вероятность появления в тексте «Капитанской дочки» форм слова «быть» [Пиотровский, 1977, с.118].

Введём обозначение: событие А= «появилась форма слова быть». Так как у каждого словоупотребления имеется одинаковая возможность быть выбранным, то выбор любой словоформы – равновозможные события. Для нахождения вероятности события А применим формулу классической вероятности, где n =29343 – число всего равновозможных несовместных событий (исходов), m=430 – число событий, благоприятных событию А. Тогда .

Вывод: 1,5% всех слов в произведении А.С. Пушкина «Капитанская дочка» составляют формы слова быть, что является отличительной характеристикой данного произведения

Статистическое определение вероятности

На практике редко можно найти вероятность события по формуле классической вероятности (из-за невозможности определения числа исходов или доказательства их равновозможности). В этих случаях используют статистическую вероятность события.

Пусть производится 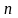одинаковых независимых испытаний.

Событие А появилось в них 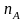раз ( - частота события А).

Тогда отношение 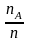называется относительной частотой события А.

При увеличении количества испытаний , относительная частота группируется около числа p (сходится по вероятности к р):

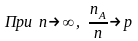
Число p называется статистической вероятностью события А.

Эта закономерность носит название устойчивости относительных частот. Устойчивость относительных частот наблюдается при многократном проведении большого числа одного и того же опыта.

Например, относительная частота глагола «быть» в русской художественной прозе при увеличении объёма исследуемого материала приобретает определённую устойчивость, приближаясь к числу 0,01.

n (объём выборки)	m (частота глагола «быть»)	Относительная частота	n (объём выборки)	m (частота глагола «быть»)	Относительная частота
10	0	0,000	6000	57	0,010
100	3	0,030	7000	71	0,010
1000	15	0,015	8000	74	0,009
2000	17	0,008	9000	88	0,010
3000	31	0,010	10000	95	0,010
4000	33	0,008	15000	153	0,010
5000	47	0,009	40000	4186	0,011

Таблица 1. Относительная частота глагола «быть»

в произведениях Пушкина, Тургенева, Бунина. [22,с.119].

Я. Бернулли в 1713 году доказал теорему, которая носит название «закона больших чисел в форме Бернулли» и объясняет близость относительной частоты к числу р, которое и является истинной вероятностью события А: как бы ни было мало число 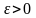_, , где р - вероятность события А в каждом отдельном испытании. Говорят, что относительная частота сходится по вероятности к вероятности этого события:

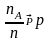
В лингвистике часто за приближённое численное значение статистической вероятности принимается при большом количестве испытаний либо сама относительная частота события А, либо некоторое число, близкое к этой относительной частоте (например, среднее арифметическое относительных частот, полученных из нескольких, достаточно больших серий испытаний). Этот подход имеет практическое значение для прикладных лингвистических исследований, например, при составлении частотных словарей.

Пример. Исследуется частотность употребления частей речи в прозе К. Федина. Взято 10 однородных фрагментов по 500 знаменательных слов каждая. Получены следующие частоты имён существительных: 182, 187, 218, 173, 158, 201, 222, 233, 213, 194. Так как количество испытаний велико (5000 слов), за приближённое значение статистической вероятности р можно взять среднюю частоту появления существительного:

Ответ: Проза Федина характеризуется частым (40%) употреблением существительных, т.е. повествование является предметным.