Вектором називається напрямлений відрізок. Позначається: , А – початок, В – кінець вектора, або .Довжина вектора або називається його модулем і позначається:

Вектори називаються рівними, якщо однаково напрямлені, а їх модулі рівні .Нульовий вектор – вектор, модуль якого дорівнює нулю, позначається: . Ортом вектора називається вектор ; , . Додавання векторів визначається за правилом паралелограма або многокутника. Сума векторів замкнутого многокутника: .

Закони додавання векторів:

Протилежні вектори. Два вектора і називаються взаємно протилежними, якщо їх модулі рівні і напрямлені протилежно

Протилежний вектору позначається - . Із . Сума протилежних векторів .

Віднімання векторів і ( позначається: ) – обернена операція додавання векторів: .

Множення вектора на скаляр. Добуток вектора і скаляра λ (позначається: λа) є вектор, який має:

Закони множення вектора на скаляр:

Вираз вектора через його модуль і орт:

Лінійна комбінація векторів. Якщо над векторами виконуються операції додавання, віднімання і множення на скаляр, то вектор вигляду

називається лінійною комбінацією заданих векторів. Тому операції додавання, віднімання і множення на скаляр називаються лінійними операціями.

Лінійні залежності між векторами. Вектори називаються лінійно залежними (незалежними), якщо їх лінійна комбінація є нуль-вектор при не всіх скалярах (при всіх скалярах) λ₁, λ₂, ..., λ_n, рівних нулю.

Колінеарні вектори. Вектори називаються колінеарними, якщо вони паралельні між собою, однаково або протилежно напрямлені.

Колінеарні вектори , і тільки колінеарні, належать одній прямій l з спільним на ній початком O.

Нехай лінійна комбінація 0 . Звідси тобто вектор колінеарний вектору .

Отже, два лінійно залежні вектори колінеарні. Якщо вектори незалежні, то лінійна комбінація: при і .

Компланарні вектори. Вектори, паралельні до однієї площини, називаються компланарними.

Компланарні вектори зі спільним початком належать площині .

Нехай три вектори - компланарні. Тоді .

Звідки 0

тобто три компланарні вектори лінійно залежні, і навпаки: три вектори лінійно залежні тоді і тільки тоді, коли вони компланарні.

Розклад вектора по трьом не компланарним векторам. Нехай - довільний вектор і вектори - не компланарні, всі вони з спільним початком. Тоді вектор єдиним способом розкладається по трьом не компланарним векторам :

,

де коефіцієнти визначаються однозначно і називаються координатами вектора .

Отже, будь-які чотири вектора простору лінійно залежні.

Метод координат.

Із однозначного розкладу будь-якого вектора по трьом не компланарним векторам дає можливість вектори, а також точки простору визначать трійками чисел (координатами).

Завдяки цьому стає можливим у векторній алгебрі застосовувати такі скалярні аналітичні методи, які заміняють операції з векторами операціями над координатами їх – трійками чисел. Тому стає можливим застосування векторної алгебри в аналітичній геометрії, взагалі, в різних областях математики.

Трійка не компланарних ортів з спільним початком в точці О називається базисом векторного простору (позначається: ( ). Будь-який вектор в цьому базисі розкладається скаляри х₁, х₂, х₃ називаються координатами вектора і позначаються:

( х₁, х₂, х₃ ).

Положення будь-якої точки М в просторі визначається в базисі ( ) радіусом-вектором

Координати радіус-вектора називаються і координатами точки М (х₁, х₂, х₃) в цьому базисі простору.

Орти відповідно визначають осі Ох, Оу, Оz косокутної системи координат Оxyz.

Таким чином, між точками простору в базисі ( ) і трійками скалярів – їх координат існує взаємно однозначна відповідність. Це перший принцип аналітичної геометрії в просторі.

Якщо не компланарні орти базису ( ) взаємно ортогональні, то вони утворюють ортогональний базис векторного простору: , який визначає прямокутну систему координат Оxyz. Орти відповідно визначають осі координат: Ох – вісь абсцис, Оу - вісь ординат, Оz – вісь аплікат. В базисі радіус-вектор точки М (х, у, z) записується у вигляді: .

На площині косокутна і ортогональна системи координат визначаються відповідно базисами: і ( ).

У базисі радіус-вектор є діагоналлю прямокутного паралелепіпеда. Тому модуль радіус-вектора дорівнює Позначимо в прямокутних трикутниках і відповідно кути: = . Косинуси цих кутів: називаються напрямленими косинусами вектора У цих трикутниках: З цих рівностей випливає:

Отже,

1.11 Лінійні операції над векторами в координатній формі.

1. Алгебраїчне додавання (сума і різниця векторів).

Нехай . Тоді

,

2. Множення вектора на скаляр

3. Визначення вектора за його початком і кінцем. Нехай (рис.1.14) Тоді

4. Модуль вектора визначається як віддаль між двома точками

5. Напрямні косинуси вектора :

1.12Поділ відрізка в заданому відношенні. Знайти точку М (х,у) яка лежить між точками М₁(х₁,у₁) і М₂(х₂,у₂) відрізка М₁,М₂ або поза ними на прямій М₁М₂ і ділить відрізок у відношенні (рис.1.15):

Якщо , то (точка М ділить внутрішньо відрізок М₁М₂).

Якщо то (точка М ділить зовнішньо відрізок М₁М₂).

Отже мають місце рівності: і

Звідси

або в координатній формі:

Зокрема, якщо λ=1, то точка М(х,у,z) – середина відрізка М₁М₂. Тоді

Тут: із відношення М₁М : ММ₂ = λ випливає, якщо довільна точка М переміщається від М₁ до М_2, то λ якщо вона переміщається в напрямі поза точкою М₂(М₁) то (рис.1.16). Отже, .

7) Знайти модуль вектора і його проекції на координатні площини і напрямні косинуси.

Розвязання. Модуль вектора дорівнює: . Проекції вектора на координатні площини дорівнюють.

Напрямні косинуси:

§ 2. Скалярний добуток двох векторів.

2.1 Кут між двома векторами з спільним початком О позначається:

Якщо , то відповідно: ; якщо один з векторів або нульовий, то кут між ними невизначений.

Означення. Скалярним добутком векторів і (позначається: ) називається число (скаляр), що дорівнює добуткові модулів цих векторів на косинус кута між ними:

Якщо , то при скалярний добуток відповідно: Якщо , то відповідно:

Вираз скалярного добутку через добуток модуля одного вектора на його проекцію другого вектора :

Закони скалярного добутку:

- переставний,

- розподільчий,

- сполучний відносно скалярного множника.

Скалярний квадрат вектора дорівнює квадрату модуля: Отже,

Кут між векторами визначається рівністю

Таблиця скалярного добутку ортів:



1 0 0

0 1 0

0 0 1

2.2 Вираз скалярного добутку через координати. Нехай . Тоді

За таблицею скалярного добутку ортів і закону сполучення відносно скалярних множників має місце рівність:

Скалярний добуток двох векторів дорівнює сумі добутків однойменних координат.

Проекція вектора на вісь :

Формула косинуса кута між векторами

Напрямні косинуси вектора

Напрямні косинуси зв’язані співвідношенням:

Модуль вектора

Необхідною і достатньою умовою перпендикулярності векторів

Приклади:

2) Задано точки А(3, 1, 0), В(0, -2, 6), С(3, -2, 0) і D(1, -2, 4). Обчислити проекцію на вісь .

Розвязання. Знаходимо . Тоді

.

3) Знайти модуль вектора

Розвязання. За формулою квадратного скаляра, дістаємо:

.

8) Обчислити довжину діагоналей паралелограма ABCD , якщо

Розвязання. Діагоналі паралелограма:

Довжина діагоналей:

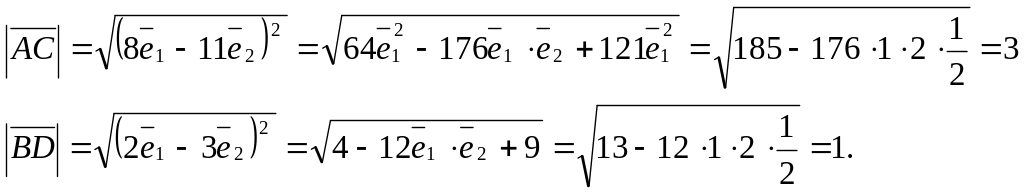
9)Обчислити скаляр: , якщо .

Розвязання. За законами скалярного добутку знаходимо:

17. Векторний добуток.

3.1 Означення. Векторним добутком векторів (позначається: ) називається вектор , який визначається трьома умовами:

1) модуль

2) вектор ;

3) напрям вектора такий, що упорядкована трійка векторів є права (має однакову орієнтацію з правим ортонормованим базисом:

3.2 Геометричні властивості векторного добутку.

1. - площі паралелограма, побудованого на векторах з спільним початком; , коли .

2. Площа S_ трикутника, визначеного векторами з спільним початком, дорівнює:

.

3. тобто , де .

4. (вектори - колінеарні, )

3.3 Алгебраїчні властивості векторного добутку.

1. відсутність переставного закону:

.

Вектори які мають однакові модулі, колінеарні, перпендикулярні до площини , але трійки: протилежної орієнтації. Отже, вектори є протилежними векторами, тобто

.

2. Сполучний закон по відношенню до скалярного множника:

3. Розподільний закон відносно додавання:

3.4 Таблиця векторних добутків ортів. У таблиці для визначення знаків користуються такою схемою:

			-
	-
		-