2 Кусочно-лінійна апроксимація статичної характеристики звт

Кусочно-лінійною апроксимацією називають заміну кривої y = f (х), заданої на інтервалі (Хn; Хv), кусочною ламаною, яка складається з N відрізків прямих. Інтервал (Хn; Хv) розбивається на N ділянок та на кожній з них нелінійна функція y=f(х) замінюється лінійною функцією.

Корегуючу ланку з кусочно-лінійною характеристикою можливо реалізувати за допомогою операційного підсилювача і набору типових діодно-резисторних схем.

3 Сплайн-апроксимація статичної характеристики звт

Кусочно-лінійна апроксимація має два суттєвих недоліка:

1. похідна КЛА- функції має розриви, що в деяких випадках може бути

недопустимим;

2. у випадках складної характеристики у=f(х) може знадобитися велика кількість лінійних ділянок N, що ускладнює схему корегуючої ланки.

Ці недоліки практично усуваються при переході від кусочно-лінійної апроксимації до СПЛАЙН – апроксимації статичної характеристики корегуючої ланки. У цьому випадку, функція у=f(х) на кожній ділянці апроксимації замінюється поліномом ступеня n >1, наприклад кубічним поліномом:

Sк(х) = Ак + Вк ·Х +Ск · Х² + Dк · Х³

Тема методи розрахунку градуювальної статичної характеристики звт

План

1 Розрахунок градуювальної статичної характеристики ЗВТ

2 Розрахунок градуювальної характеристики ЗВТ методом середніх

3 Розрахунок градуювальної характеристики ЗВТ методом найменших квадратів

4 Розрахунок градуювальної характеристики методом Асковиця

5 Розрахунок градуювальної характеристики ЗВТ методом найменших модулів

1 Розрахунок градуювальної статичної характеристики звт

Розрахунок градуювальної статичної характеристики ЗВТ зводиться до визначення в аналітичній формі залежності у=fг(х), якщо відомі значення хi, які вимірюють або встановлюють на вході ЗВТ, та деякі значення вихідного сигналу уi.

Рішення задачі проводиться в два етапи:

1. Обирають загальний вид формули у=fг(х). Для цього використовують

відому або близьку залежність х і у.

2. Знаходять такі значення коефіцієнтів q1,q2,…qn за яких залежність у=fг(х;q1,q2,…qn) забезпечує найкращу відповідність між розрахунковим і експериментальними даними та оцінюють ступінь цієї відповідності, тобто розраховують похибку апроксимації (у формі максимальної зведеної похибки апроксимації або у формі середньоквадратичної зведеної похибки апроксимації).

Якщо похибка апроксимації перевищує допустиму похибку, робиться висновок про те, що математична модель ЗВТ, яка представлена рівнянням у=fг(х;q1,q2,…qn), побудована невірно та розроблюється нова модель.

2 Розрахунок градуювальної характеристики звт методом середніх

При використанні методу середніх, параметри q1,q2,…qn прагнуть вибрати так, щоб виявилася рівною нулю середня похибка апроксимації. Для цього складають систему N рівнянь

у=fг(х;q1,q2,…qn) – у1 = e1,

у=fг(х;q1,q2,…qn), – у2 = e2,

у=fг(х;q1,q2,…qn) – уN = eN,

де eі – похибка апроксимації в точці хi.

Праворуч цих рівнянь накладають умову:

N

∑ еі = 0

і=1

Оскільки число рівнянь, що співпадає із числом експериментальних точок, звичайно більше числа параметрів, всі рівняння системи розбивають на n груп рівнянь. У кожній такій групі рівняння почленно складають один з одним.

Вирішують цю систему рівнянь, знаходять значення параметрів.

Приклад

У таблиці показані експериментальні точки (хі, уi). Необхідно методом середніх визначити параметри А,В,С градуювальної характеристики у=Ах²+Вх+С.

хі	7	12	17	22	27	32	37
уі	83,7	72,9	63,2	54,7	47,5	41,4	36,3

Рішення: підставляючи табличні дані в рівняння градуювальної характеристики ЗВТ, одержуємо систему, що складається із семи рівнянь

49А +7 В+С- 83,7 = е1,

144А+ 12В + С – 92,9 = е2,

289 А+ 17В + С – 63,2 =е3

_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

484 А + 22В + С – 54,7 = е4,

729А + 27В + С – 47,5 = е5,

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

1024 А + 32В + С – 41,4 = е6,

1369 А + 37В + С - 36,3 = е7

Оскільки невідомих параметрів три (n = 3), розіб’ємо ці системи рівнянь на три групи. Почленно складаємо рівняння в кожній групі, одержуємо нову систему

484А+ 36В+3С = 219,8,

1213А + 49В +2С = 102,2,

2393А + 69В+ 2С = 77,7

Вирішуємо цю систему рівнянь: А= 0,0235, В= - 2,6115, С= 100,8295.

Отже градуювальна статична характеристика ЗВТ має вигляд

У= 0,0235 х² - 2,6115х + 100,8295

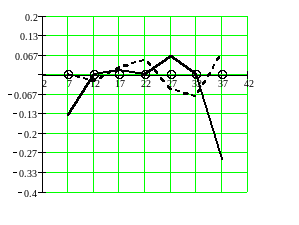
Суцільною кривою показаний розподіл похибки, получений методом інтерполяції. Використання метода середніх (на графіку – пунктирна) знижує максимальну похибку апроксимації.