Вопросы для самоконтроля:
1. Дайте определение вектора.
2. Дайте определение скалярной величины.
3. Линейные операции над векторами. Длина вектора.
4. Дайте определение базиса.
5. Разложение вектора по базису.
6. Определение скалярного произведения векторов.
7. Свойства скалярного произведения векторов.
8. Скалярное произведение векторов в векторной и координатной формах.
Лекции 5-6. Различные виды уравнения прямой
Уравнение прямой с угловым коэффициентом
у = k x + b, (1)
где
,
- называется угловым коэффициентом
у М (х,у)
у-b
α
N (0, b)
x
α
0
х
Рисунок 1. Уравнение прямой с угловым коэффициентом
Пример
1.
Уравнение
перепишем в виде
Следовательно,
это уравнение определяет прямую с
угловым коэффициентом
,
пересекающую ось
в точке с координатой
.
Для того, чтобы изобразить эту прямую, найдем ее точку пересечения с осью ОХ. Подставив в уравнение у=0, получим, что х=2,5.
2)Уравнение прямой через данную точку (х0,у0) с угловым коэффициентом k имеет вид:
(2)
С помощью угловых коэффициентов определяются углы между прямыми.
Теорема.
Тангенс
угла
между прямыми
и
определяется формулой:
(3)
Условия параллельности и перпендикулярности прямых:
прямые
и
параллельны
в том случае, когда
(4)
прямые
и
перпендикулярны,
когда
(5)
Пример
2.
Для
прямой
запишем уравнения прямых
||
и L3
перпендикулярной
,
проходящих через точку М0
(1,2).
Прямая имеет тот же угловой коэффициент, что и , т.е. k2=3,
поэтому ее уравнение имеет вид: у – 2 = 3( х - 1), т.е. у=3х - 1
Прямая L3 имеет угловой коэффициент k2=-1/k, т.е. k2=-1/3,
ее уравнение записывается в виде: у – 2 = -1/3( х - 1), т.е. у=-1/3х +7/3
3) Параметрическое уравнение прямой на плоскости имеет вид:
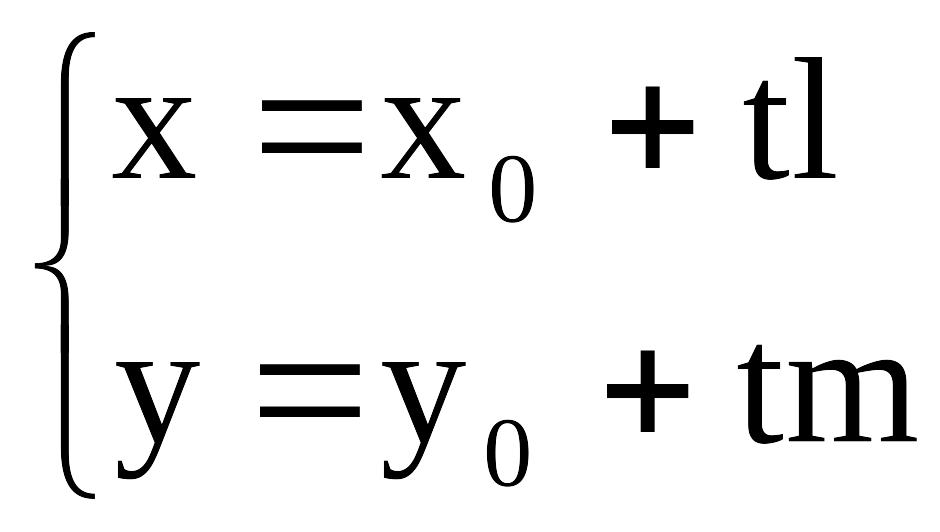(6)
4) Уравнение прямой с направляющим вектором имеет вид
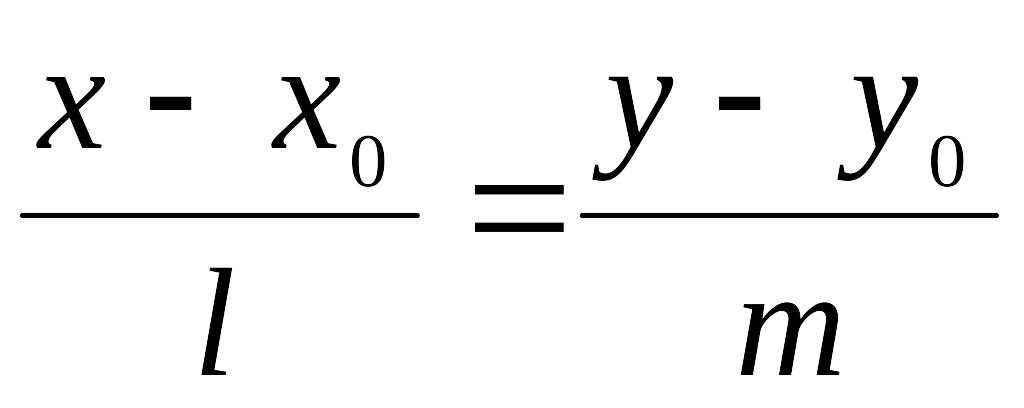(7)
Любой ненулевой вектор а(l,m) на прямой L называется направляющим. Этот вектор является базисным вектором этой прямой.
Пример
3.
Напишем уравнение прямой, проходящей
через точку
параллельно вектору
.
Подставим координаты точки и вектора
в уравнение, получим
;
x
- 1 = (-1)(y
- 2); х+y
– 3 = 0; y
= - х+3
5)
Уравнение
прямой, проходящей через две заданные
точки
М0(х0,у0)
и
имеет вид:
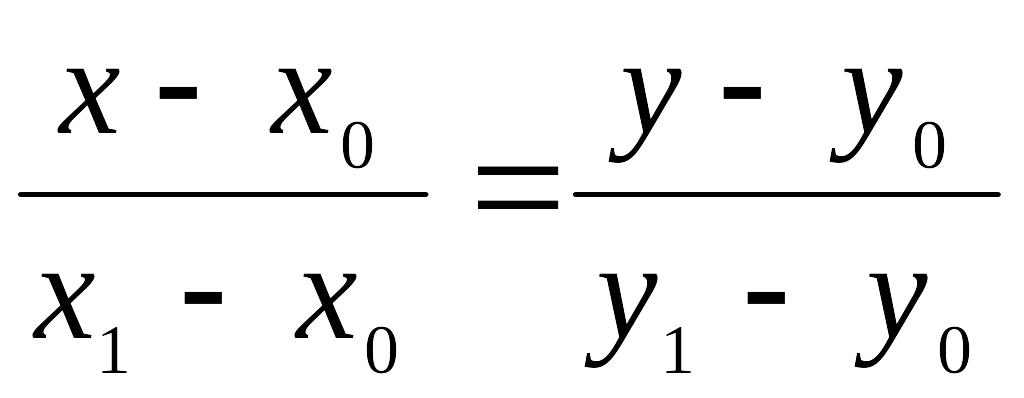(8)
Пример
4.
Запишем
уравнение прямой, проходящей через
точки
и
.
Подставив координаты точек в уравнение,
получим:
6)
Общее уравнение
прямой имеет вид:
(9)
Если
,
то
,
что есть уравнение прямой с угловым
коэффициентом.
Если
,
то
получим:
- это уравнение определяет вертикальную
прямую, проходящую через точку
на оси
.
7)
Вектор
,
перпендикулярный прямой L,
называется нормальным
вектором этой
прямой.
Теорема
о
нормальном векторе прямой.
Вектор
с
координатами
является нормальным
для прямой L с уравнением
на плоскости
(см. рисунок 2).
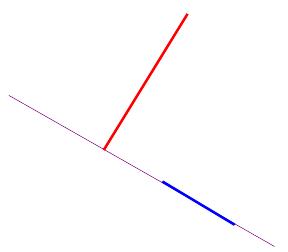
M0
M1 L
Рисунок 2.
Пример 5. Найти нормальный вектор для прямой y = 2x + 3
Уравнение
прямой в общем виде: 2x
– y
+ 3 = 0. Отсюда
= (2,-1).
Следствие
1.
Косинус
угла
между
прямыми
:
x
+
y+
=
0
и
:
x
+
y
+
=0
с
нормальными векторами
и
находится
по
формуле:
cos
=
=
(10)
Следствие 2. Эти прямые перпендикулярны только в том случае, когда
(11)
Следствие 3. Эти прямые параллельны только в том случае, когда
(12)
Прямые и совпадают, если
(13)
Пример
6.
Найдем
угол между прямыми
и
Здесь
(1,2),
(-2,1) и cos
=
,
следовательно, эти прямые перпендикулярны.
8)
Пусть прямая L
проходит через точку
(
)
перпендикулярно
вектору
тогда ее уравнение
имеет
вид:
(14)
Это уравнение называется уравнением прямой с нормальным вектором.
Пример
7.
Дана
прямая
и точка
Запишем
уравнения прямых
и
,
проходящих через точку
,
где
║
а
.
Пусть
- нормальные векторы прямых
.
Поскольку
║
,
то можно положить
=(2,3).
Запишем уравнение прямой с этим нормальным вектором, проходящей через точку , получим уравнение :
Поскольку
,
то
║
,
следовательно, вектор
(2,3)
является направляющим для
и ее уравнение имеет вид:
и
