Степенные ряды
Степенным рядом называется функциональный ряд вида
,
(1)
где
постоянные
называются коэффициентами
степенного ряда.
n-ным
членам
степенного ряда называют член
,
хотя он стоит в степенном ряде на n
+1- месте.
Теорема
Абеля. Если
степенной ряд (1) сходится
в точке
,
то он сходится абсолютно
в интервале (-
)
т.е. при всяком х, удовлетворяющем
условию
; если степенной ряд (1) расходится
точки
,
то он расходится
при всяком х, удовлетворяющим условию
.
Из теоремы Абеля следует, что все точки сходимости расположены от начала координат не дальше, чем любая из точек расходимости и заполняют некоторый интервал с центром в начале координат.
Для
каждого степенного ряда, имеющего
точки сходимости и расходимости,
имеются положительное число R, что
для всех х, удовлетворяющих условию
,
ряд сходится
а для всех х, удовлетворяющих условию
,
ряд расходится.
И
это число R называется радиусом
сходимости
степенного ряда (1), а интервал (-R,R)
–интервалом
сходимости.
При R=
х
ряд может сходиться, может и расходиться.
Радиусы сходимости степенных рядов устанавливаются следующими способами.
Составляется
ряд из абсолютных величин членов степного
ряда (1):
(2)
Для определения сходимости ряда с положительными членами (2) применяется признак Даламбера. Пусть существует предел
.
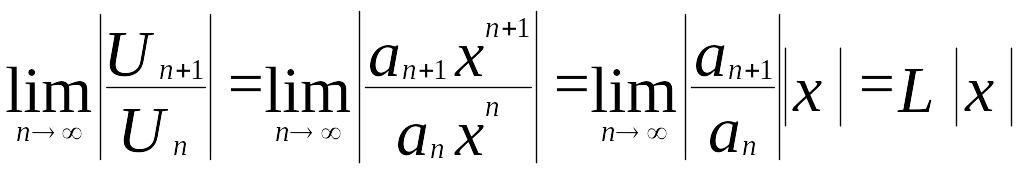Тогда
по признаку Даламбера ряд (2) сходится
при
,
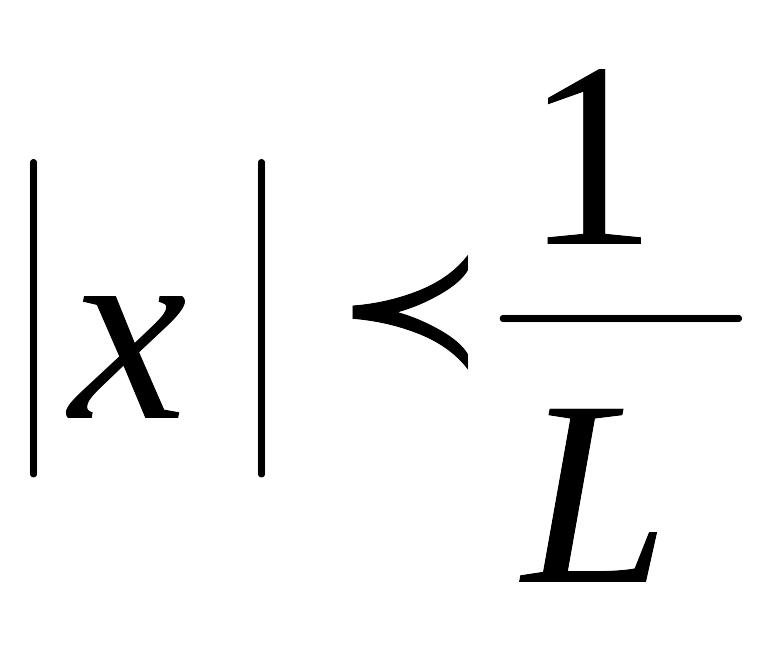и расходится при
.
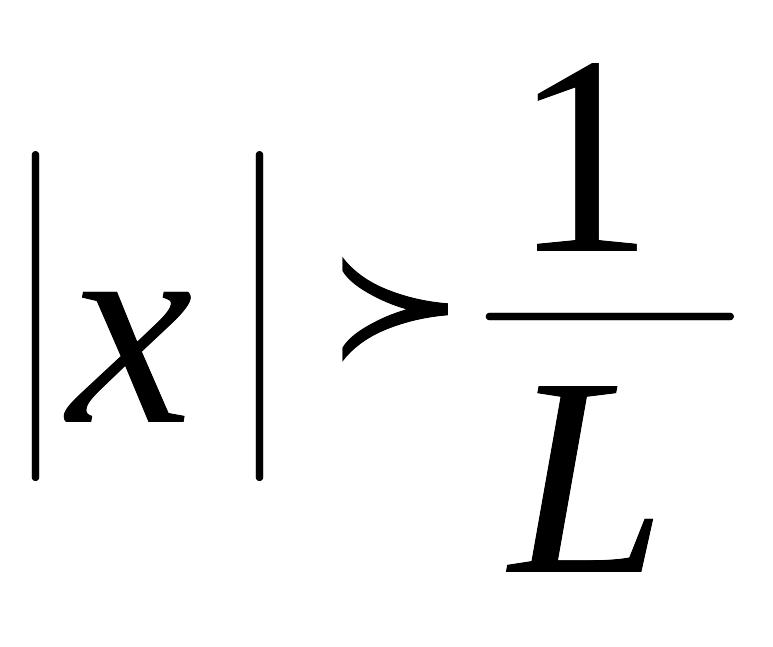Следовательно, исходный ряд (1)
сходится абсолютно, если
, и расходится если
.
Поэтому интервалом сходимости степенного ряда (1) будет (-R,R) , где
.
(3)
Радиус сходимости степенного ряда (1) определяется также с применением признаком Коши по формуле
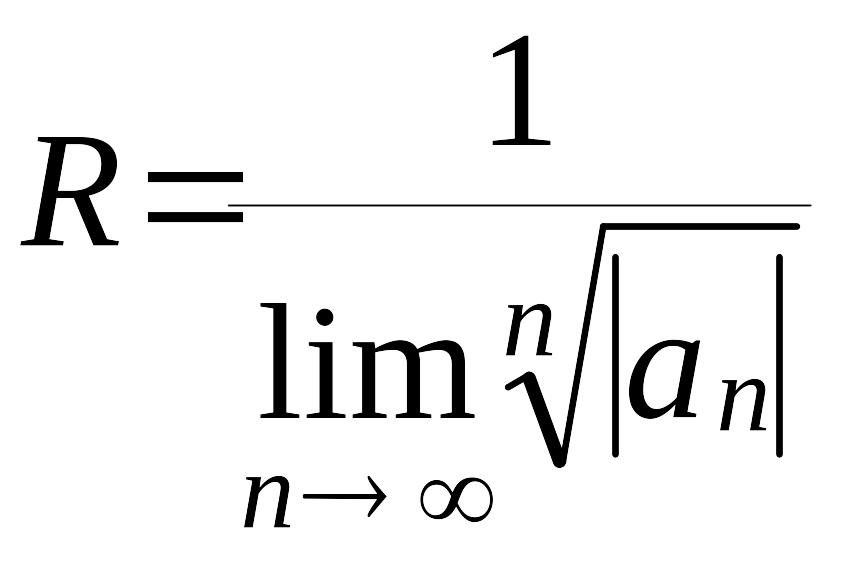(4)
Теорема 1. Степенные ряды можарируемы на любом отрезке [-α, α], целиком лежащем внутри интервала сходимости (- R,R).
Теорема 2. Сумма можарируемого степного ряда S(x) есть функция, имеются внутри интервала сходимости (-R,R) производные любого порядка, каждая из которых есть сумма ряда, полученного почленным дифференцированием данного ряда соответствующее число раз, при этом каждый ряд имеет один и тот же интервал сходимости (-R,R).
Теорема 3. Можарируемый степенной ряд (1) можно почленно интегрировать, если пределы интегрирования α, β лежат внутри интервала сходимости (-R,R) , и интеграл от суммы S(x) ряда равен сумме интегралов о членов ряда.
Степенным рядом также называется функциональный ряд вида
(5)
ряд (5) есть степенной ряд по степеням двучлена (x-a).
Для определения области сходимости ряда (5) вводится замена переменного x-a=X и он принимает вид
(6)
Пусть интервал сходимости ряда (6) есть (-R,R). Тогда интервалом сходимости данного ряда (5) будет интервал (a-R, a+R) с центром в точке a. Все свойства степенного ряда (1) внутри интервала сходимости (-R,R) сохраняется и для степенного ряда (5) внутри интервала сходимости (a-R, a+R).
Вопросы для самоконтроля
1.Понятие числового ряда.
2.Свойства сходящихся рядов.
3.Необходимое условие сходимости ряда.
4.Сходимость положительных рядов.
5.Первая теорема сравнения
6.Вторая теорема сравнения.
7.Достаточные признаки сходимости положительных рядов.
8. Признак Даламбера
9.Признак Коши
10.Знакопеременные ряды.
11. Теорема Лейбница
12.Абсолютная и условная сходимости
13.Функциональные ряды
14.Степенные ряды.
15.Теорема Абеля