
- •Линейная алгебра и элементы аналитической геометрии Лекция 1-2. Матрицы. Определители
- •Матрицы, виды матриц
- •Линейные операции над матрицами, свойства матриц
- •Умножение матриц
- •Обратная матрица. Необходимое и достаточное условие существования обратной матрицы.
- •Ранг матрицы
- •Метод окаймляющих миноров
- •Метод элементарных преобразований
- •Свойства определителей:
- •Вычисление определителей
- •Лекция 3. Системы линейных алгебраических уравнений (слау)
- •Совместность систем уравнений. Теорема Кронекера – Капелли
- •Правило Крамера
- •Метод обратной матрицы
- •Системы m линейных уравнений с n неизвестными. Метод Гаусса. Однородная слау
- •Вопросы для самоконтроля:
- •Лекция 4. Векторы
- •Скалярное произведение векторов в r3 и его свойства
- •Скалярное произведение в координатной форме
- •Свойства скалярного произведения
- •Вопросы для самоконтроля:
- •Лекции 5-6. Различные виды уравнения прямой
- •9) Уравнение прямой в отрезах
- •10) Нормальное уравнение прямой
- •Общее уравнение плоскости в пространстве и его частные случаи
- •14) Уравнение плоскости с нормальным вектором:
- •Понятие функции. Способы задания и свойства функции
- •Односторонние пределы
- •Основные теоремы о пределах.
- •Замечательные пределы
- •Лекция 8. Производная и дифференциал функции
- •Механический смысл производной.
- •Геометрический смысл производной
- •Правила дифференцирования (Производная суммы, произведения и частного)
- •Дифференцирование неявных функций
- •Логарифмическое дифференцирование
- •Дифференциал функции
- •Лекция 9. Приложения производной. Производные и дифференциалы высших порядков. Исследование функций
- •Приложения производной.
- •2. Производные и дифференциалы высших порядков
- •Правило Лопиталя
- •3. Исследование функций
- •Асимптоты
- •Общая схема исследования функции:
- •Вопросы для самоконтроля:
- •Непрерывность функции двух переменных
- •Частные производные
- •Частные производные высших порядков.
- •Полный дифференциал функции
- •Применение полного дифференциала к приближенным вычислениям
- •Формула Тейлора
- •Необходимое и достаточное условие экстремума.
- •Необходимое условие экстремума
- •2) Достаточное условие экстремума
- •Лекция 12. Интегральное исчисление Неопределенный интеграл
- •Основные свойства неопределенного интеграла
- •Интегрирование по частям
- •Интегрирование дробно - рациональных выражений. Интегрирование тригонометрических выражений и иррациональных функций
- •Интегрирование функций, содержащих квадратный трехчлен.
- •Интегрирование дробно - рациональных выражений.
- •3. Интегрирование тригонометрических выражений
- •Универсальная подстановка
- •4. Интегрирование иррациональных функций
- •Задания
- •Лекция 13. Определённый интеграл и его приложения. Несобственные интегралы
- •Свойства определенного интеграла
- •Формула Ньютона – Лейбница
- •Замена переменной в определенном интеграле
- •Нахождение определенного интеграла по частям
- •Приложения определенного интеграла Вычисление площадей плоских фигур
- •Вычисление длины дуги кривой
- •Вычисление объемов тел
- •Несобственные интегралы
- •Признаки сходимости несобственных интегралов
- •Задания
- •Лекция 14 Дифференциальные уравнения. (Дифференциальные уравнения. Общие понятия и определения. Задача Коши. Уравнения с разделенными переменными. Уравнения с разделяющимися переменными)
- •Лекция 15. Теория рядов
- •§1 Понятие числового ряда
- •§2 Свойства сходящихся рядов
- •§3 Необходимое условие сходимости ряда
- •§4 Сходимость положительных рядов
- •§5 Теоремы сравнения рядов.
- •§6 Достаточные признаки сходимости положительных рядов
- •Теорема 3. (Интегральный признак сходимости ряда).
- •§6 Знакопеременные ряды. Теорема Лейбница
- •Абсолютная и условная сходимости
- •Функциональный ряд
- •Мажорируемые ряды
- •Степенные ряды
Несобственные интегралы
Непременными условиями существования определенного интеграла являются требования:
- промежуток интегрирования [а,b] конечный,
- подынтегральная функция непрерывна на отрезке [а,b].
При нарушении хотя бы одного из этих условий определенный интеграл теряет свой собственный смысл и превращается в так называемый несобственный интеграл.
В зависимости от того, какое из указанных условий нарушается, различают несобственные интегралы I и II-рода.
К несобственным интегралам 1-рода относятся интегралы с бесконечными пределами интегрирования:
|
(1) |
Говорят, что первые два несобственных интеграла из (1) сходятся, если существуют соответствующие конечные пределы от определенного интеграла:
|
(2) |
Последний из несобственных интегралов (по всей числовой оси) будет сходящимся только в том случае, когда сходятся оба слагаемых в правой части равенства.
Заметим, что несобственный интеграл есть предел определенного интеграла, а не интегральной суммы.
Следовательно, они обладают основными свойствами определенного интеграла.
Пример 1.

В зависимости от того, где подынтегральная функция терпит разрыв: в начале, в конце или во внутренней точке отрезка, рассматриваются несобственные интегралы II-рода:

О сходимости этих интегралов можно сказать то же самое, что для собственных интегралов 1-рода:
Пример
2.

Признаки сходимости несобственных интегралов
Теорема
1.
(Первый признак сравнения) Пусть
функции
и
![]() непрерывны в промежутке
непрерывны в промежутке
![]() и в этом промежутке выполняется
неравенство
и в этом промежутке выполняется
неравенство
![]() .
.
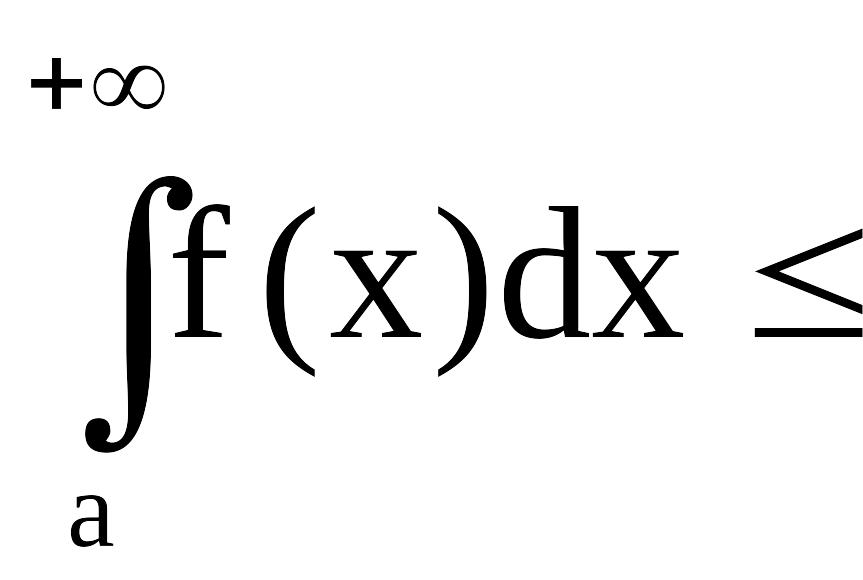
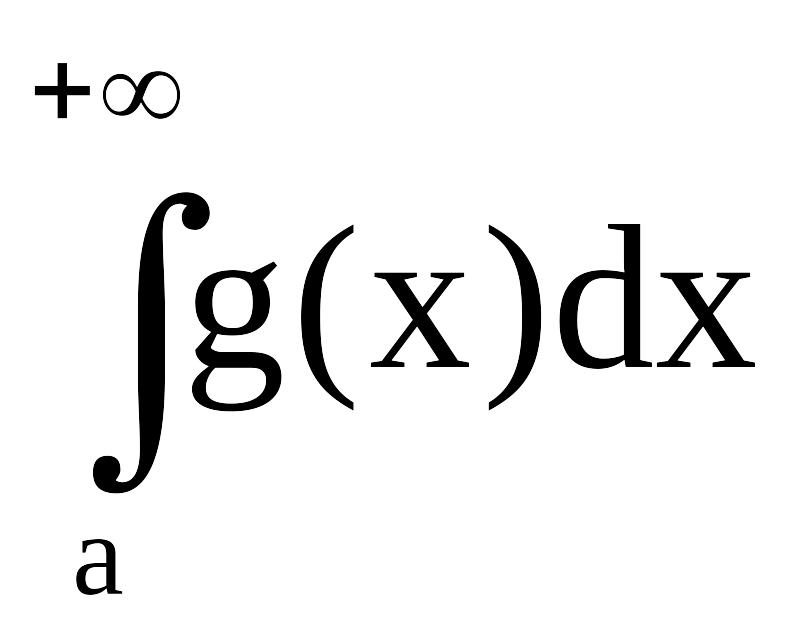
а)
Если
сходится,
то
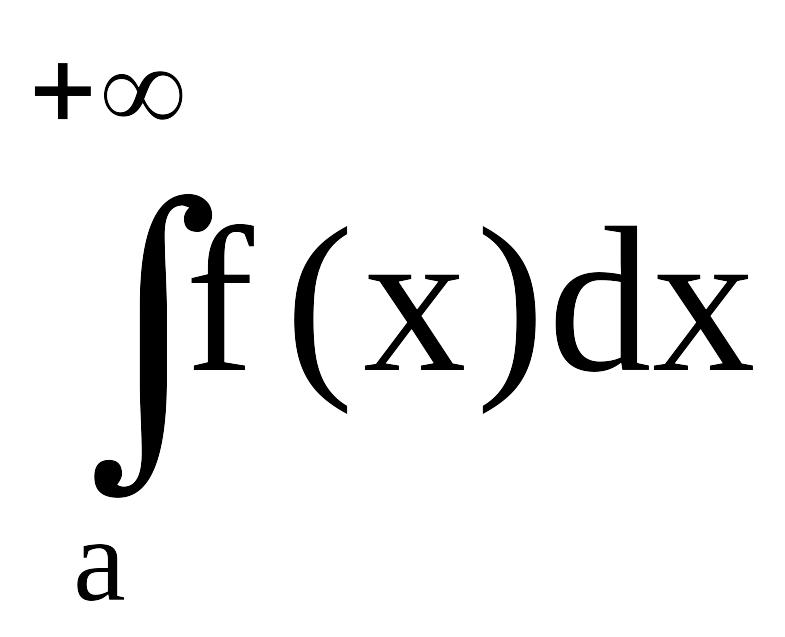 также
сходится
также
сходится
б)
Если
расходится,
то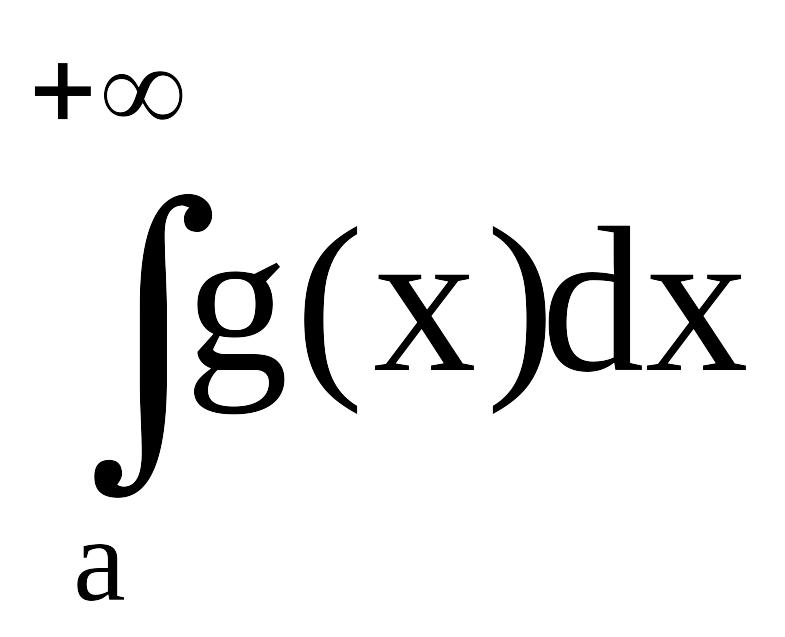 также
расходится.
также
расходится.
Пример
3.
Исследуем сходимость интеграла
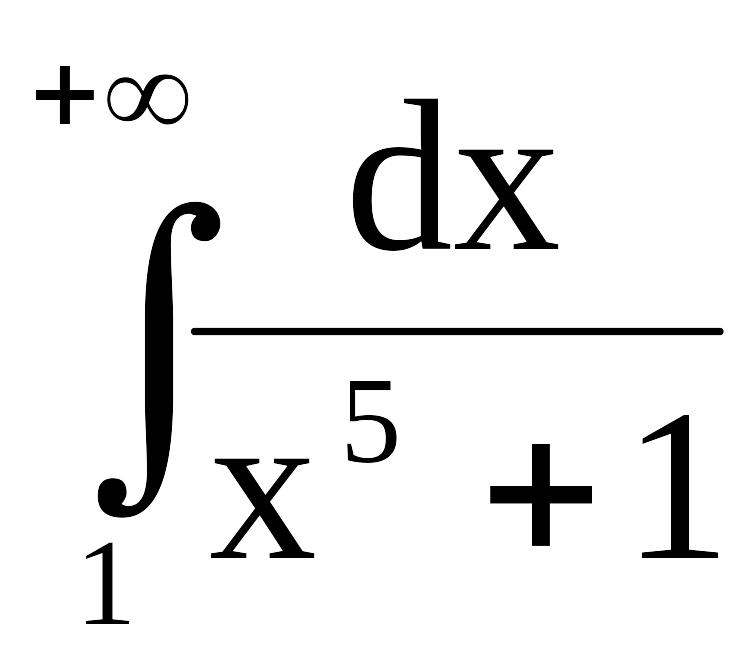 .
.
![]() ,
,
 .
.
Тогда по первому признаку сравнения исходный интеграл сходится.
Теорема
2.
(Предельный признак сравнения) Пусть
неотрицательные в промежутке
функции
,
непрерывны в этом промежутке и существует
предел
![]() ,
который не равен 0 и
,
который не равен 0 и
![]() .
Тогда
несобственные интегралы
и
сходятся и расходятся одновременно.
.
Тогда
несобственные интегралы
и
сходятся и расходятся одновременно.
Пример
4.
Исследуем сходимость
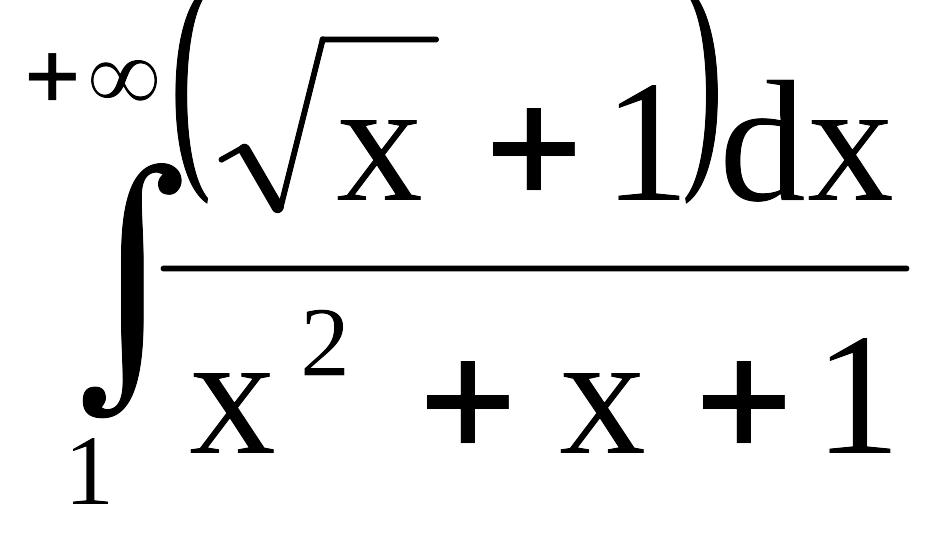 .
.
![]()
Поскольку

и интеграл
 -
сходится,
то исходный интеграл также сходится по
предельному признаку сравнения.
-
сходится,
то исходный интеграл также сходится по
предельному признаку сравнения.
Задания
|
Вычислить определенный интеграл: 1.
4.
7.
8.
Вычислить несобственный интеграл, или установить его расходимость: 10.
12.
14.
|
16.Вычислить площадь фигуры, ограниченной линиями
![]()
![]()
17. Вычислить площадь фигуры, ограниченной линиями
![]()
18. Вычислить площадь фигуры, ограниченной первой аркой циклоиды
![]() и
осью
и
осью
![]()
![]()
19. Вычислить площадь фигуры, ограниченной петлей линии
![]()
![]()
20.
Вычислить длину дуги параболы
![]() между точками с
между точками с
абсциссами
![]() и
и
![]()
![]()
21.Вычислить
длину астроиды![]()
![]()
22.Вычислить
длину кардиоиды
![]()
![]()
Вопросы для самоконтроля:
1.Первообразная, неопределенный интеграл. Их свойства.
2.Непосредственное интегрирование.
3.Замена переменной в неопределенном интеграле.
4.Подведение под знак дифференциала.
5.Интегрирование по частям в неопределенном интеграле.
6.Интегрирование рациональных выражений. Метод неопределенных коэффициентов.
7.Интегрирование тригонометрических выражений.
8.Интегрирование тригонометрических выражений с помощью универсальной подстановки.
9.Определенный интеграл: определение и геометрический смысл.
10.Свойства определенного интеграла.
11.Формула Ньютона-Лейбница.
12.Замена переменной в определенном интеграле. Подведение под знак дифференциала.
13.Формулы вычисления площадей плоских фигур в декартовых и полярных координатах.
14. Формулы вычисления длины дуги кривой, объема тела.
15. Несобственный интеграл. Признаки сходимости.
Литература
1. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. - М.: Наука, 1988.-190 с.
2. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. -М.: Наука, 1988.- 430 с.
3. Пискунов Н.С. Дифференциальное и интегральное исчисление. Т.1,2- М.: Наука, 1985.-270 стр.
4.Сборник индивидуальных заданий по математике. Под редакцией
Рябушко А.П., Ч. 1,2,3 Минск: высшая школа, 2001.- 400 с.
5. Искакова С.К.,Мустахишев К.М. Интегральное исчисление функции одной переменной: Учебное пособие.- Алматы: «Эверо», 1999.- 64 с.
6. Искакова С.К., Мустахишев К.М. Интегральное исчисление функций многих переменных. Векторный анализ.- Алматы:


 2.
2.
 3.
3.
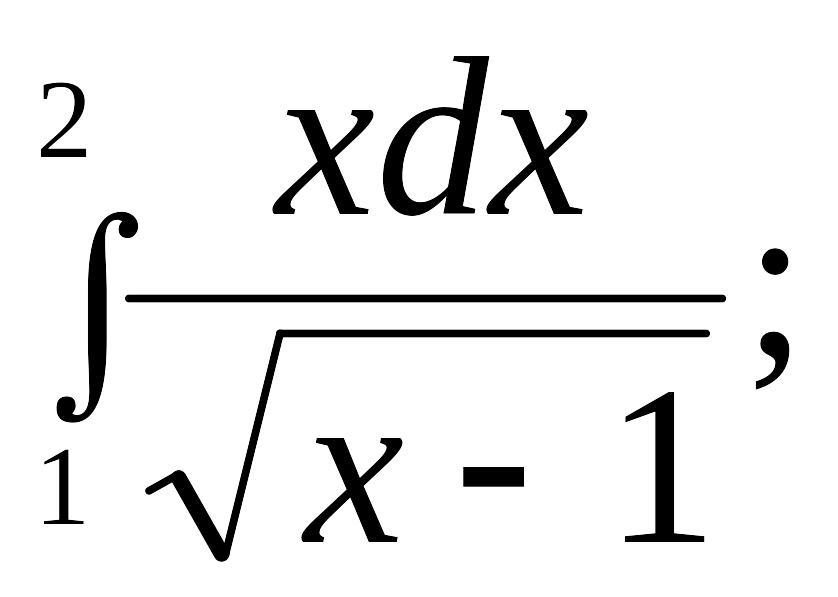
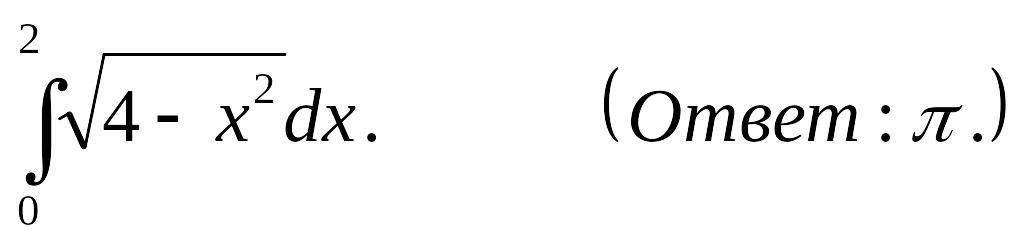
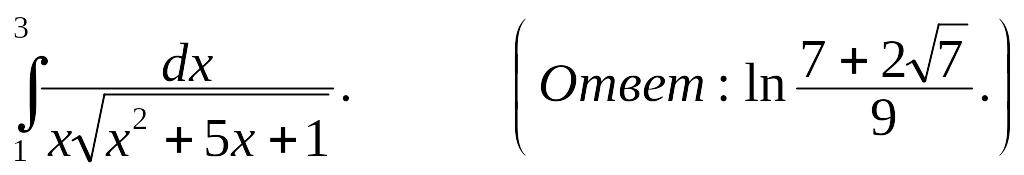
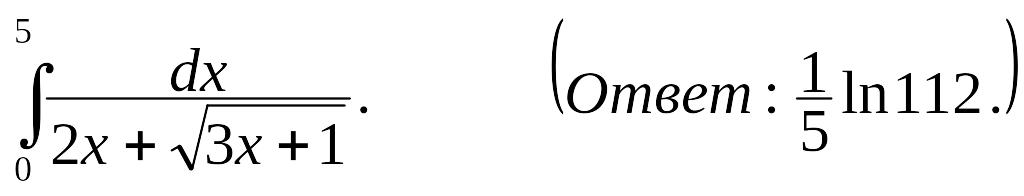
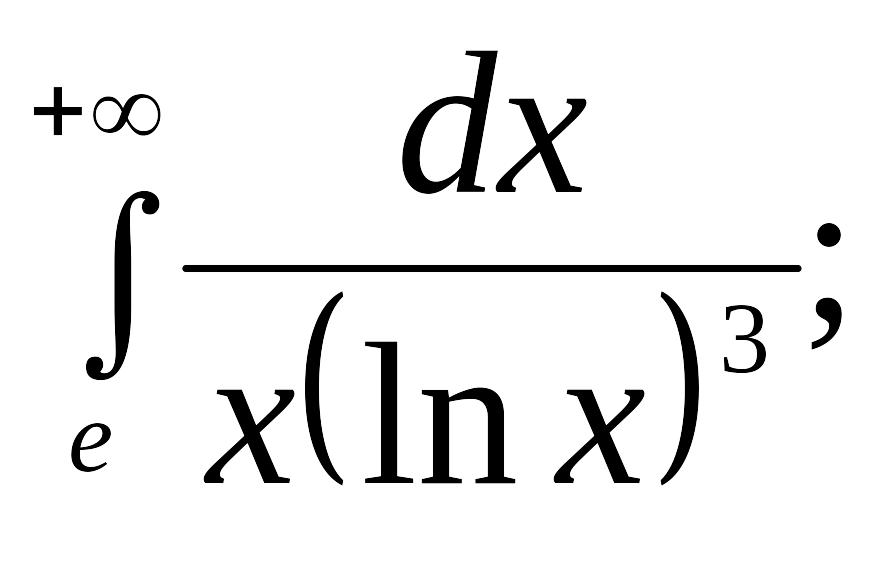 (Ответ:
0,5)
11.
(Ответ:
0,5)
11.
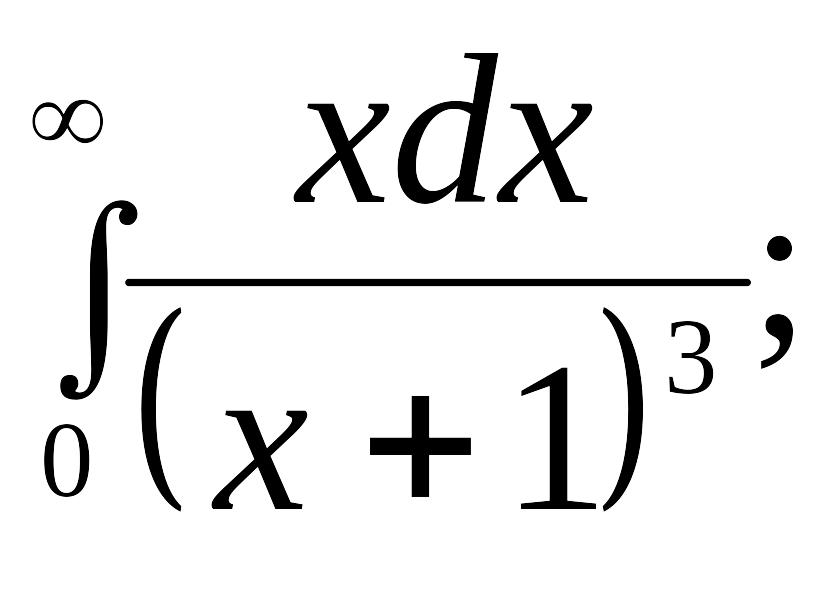 (Ответ:
0,5)
(Ответ:
0,5)