3. Интегрирование тригонометрических выражений
I.
Рассмотрим интегралы, содержащие
подынтегральные функции типа
,
где m,
n
– const.
Подынтегральные функции приводятся к сумме первых степеней синусов и косинусов с помощью формул:
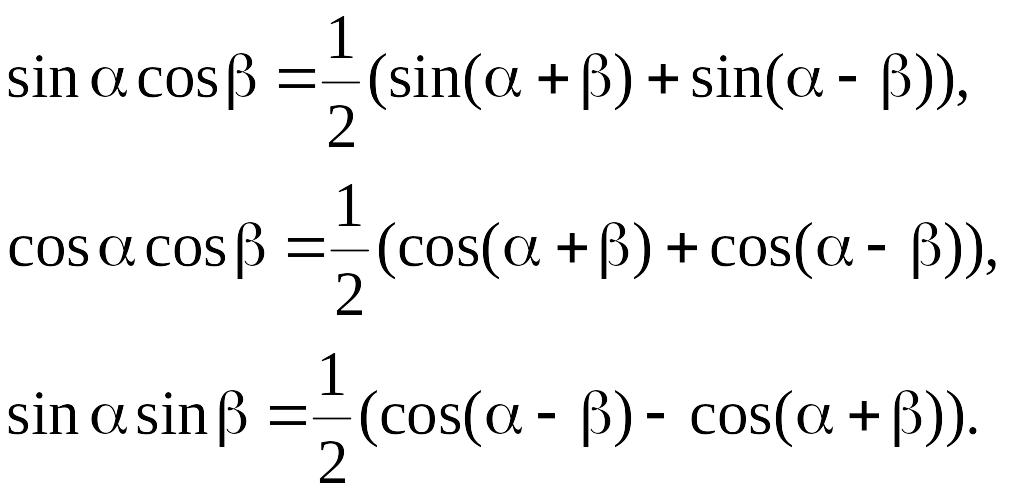(3)
Пример 5.
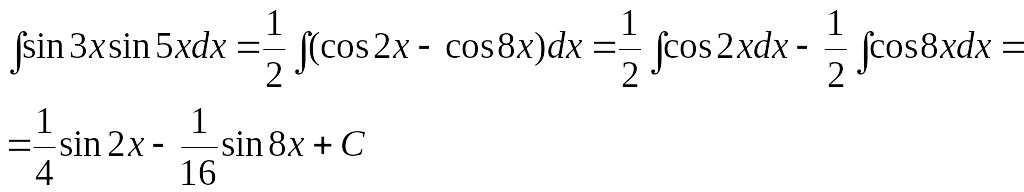
II.
Интегралы вида
,
где m
и n
–целые числа вычисляются просто в
четырех случаях.
1 случай. Если m или n – нечетные, целые, положительные числа, то отделяя от нечетной степени один сомножитель и выражая с помощью формулы sin2x+cos2x=1 оставшуюся четную степень, применяют подстановку cosx=t или sinx=t.
Пример 6.
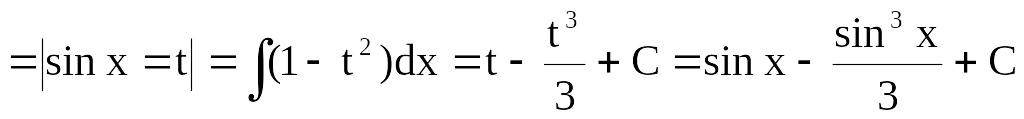
Пример 7.
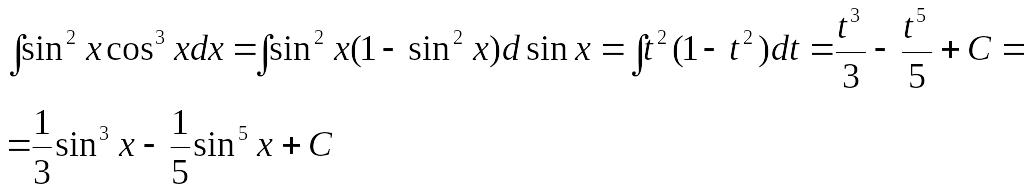
2 случай. Если m, n – четные, целые, положительные числа, то можно понизить степень с помощью преобразований:
2sinxcosx=sin2x
,
(4)
Пример 8.
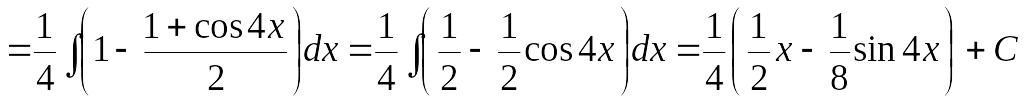
3 случай. Если m+n–четное, отрицательное число, то применяется подстановка
tg
x = t, x = arctg t,
,
,
(5)
которая сводит этот интеграл к табличному.
4 случай. Если m+n=0, где m,n –целые числа, то есть степени sinx, cosx равны по величине и противоположны по знаку, применяется подстановка
tg x = t, x = arctg t, , tg2x=sec2x-1, sec2x=1/cos2x или
ctg x t, x=arcctg t, ctg2x=cosec2x-1, cosec2x=-1/sin2x
Пример 9.
∫
.
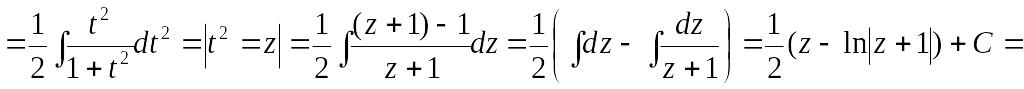
Универсальная подстановка
III.
Интегралы вида
,
(где R-
рациональная функция) приводятся к
интегралу от рациональной функции
подстановкой
,
,
Пример
10.
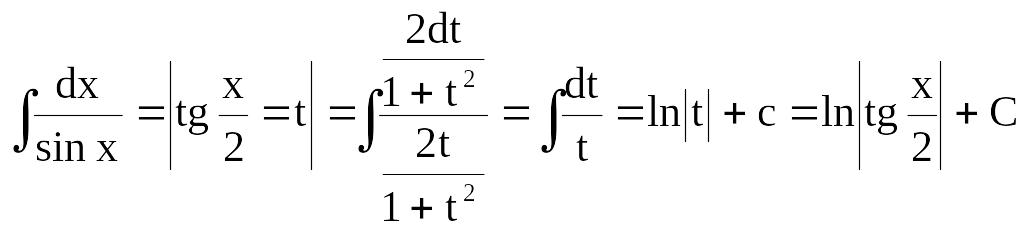
Пример
11.
=
|
|
=
Хотя
данный метод формально может быть
применен к любым указанным интегралам,
в случаях, когда функция содержит
переменные
или
в
степени выше первой,
часто получаются достаточно громоздкие
выражения.
В этих случаях разумнее применять следующие частные подстановки:
.
Если подынтегральная функция является
нечетной
по синусу,
т. е.
,
то выгодна подстановка
.
20.
Если подынтегральная функция является
нечетной
по косинусу,
т. е.
,то
выгодна подстановка
.
.
Если
подынтегральная функция является четной
по синусу и косинусу,
т.е.
,
то
применяется подстановка
,
,
,
sinx=t∕√1+t2,
cosx=
1∕√1+t2
4. Интегрирование иррациональных функций
I.
Интегралы вида
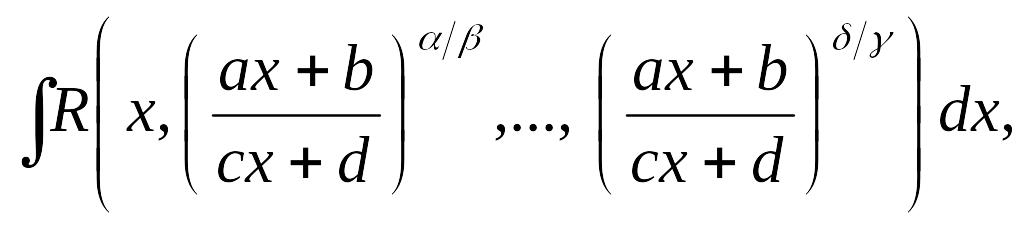
где
R–
рациональная функция, a,b,c,d
–
действительные числа,
-
натуральные числа, сводятся к интегралам
от рациональной функции с помощью
подстановки
.
(k-
наименьшее общее кратное знаменателей
дробей (НОК)
).
В
частности, интеграл вида
приводится
к интегралу от рациональной функции
новой переменной с помощью подстановки
.
Пример
12.
Найти интеграл
.
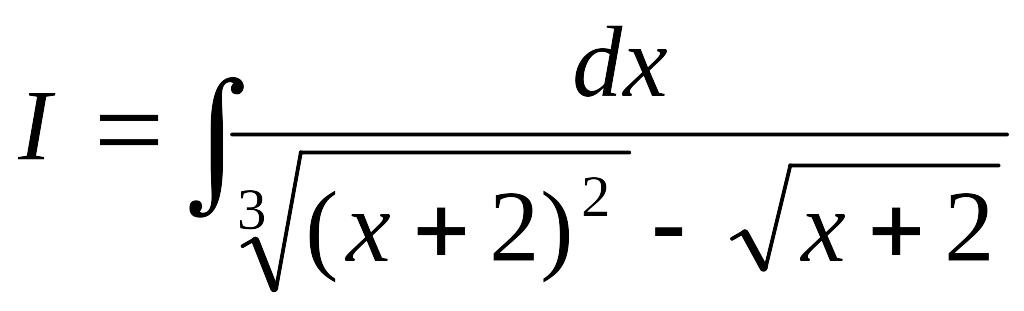НОК
есть 6.
Поэтому
полагаем
Следовательно,
.
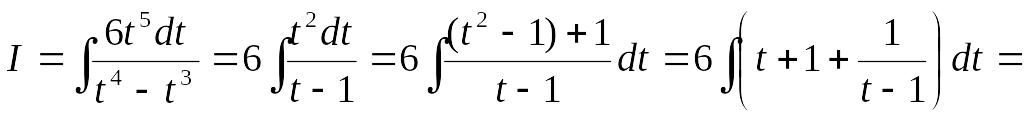
II. Интегралы вида
1)
,
2)
,
3)
приводятся к интегралам от функций, рационально зависящих от тригонометрических функций, с помощью следующих соответствующих тригонометрических подстановок:
;
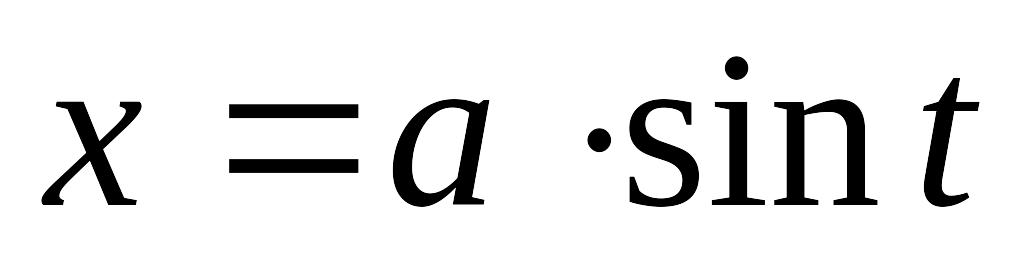2)
;
3)
.
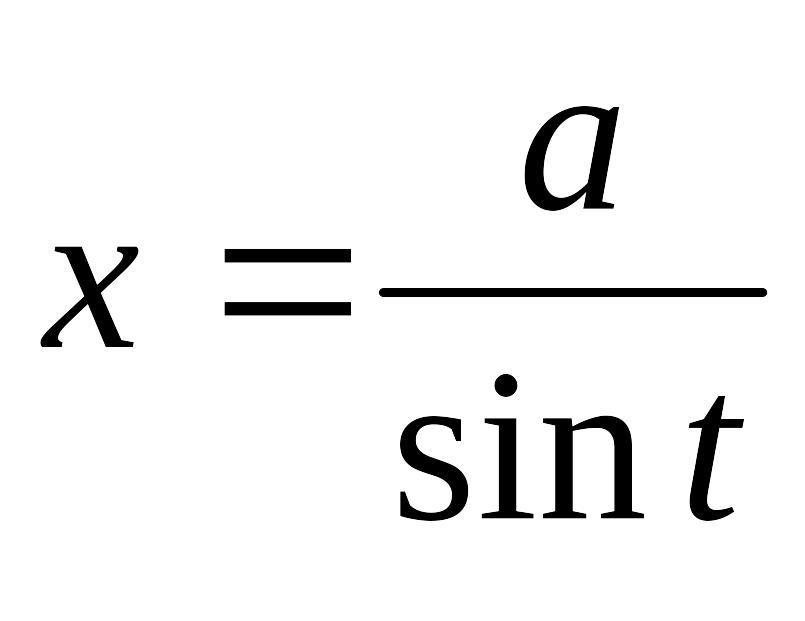III.
Интегралы
вида
приводятся к интегралам вида II.
Выделив под радикалом полный квадрат и сделав подстановку , интегралы указанного вида приводятся к уже рассмотренным интегралам II.
Пример
13.
Найти
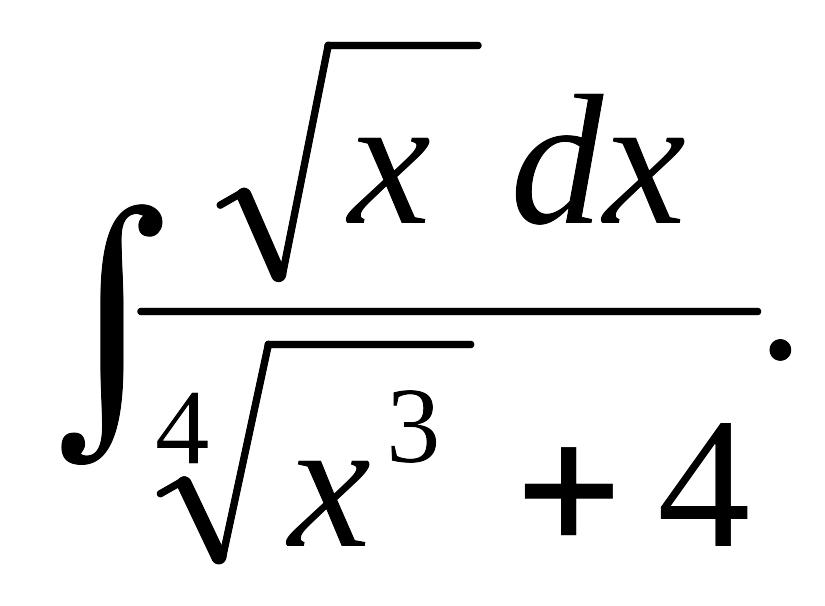
Так
как НОК (2, 4) = 4, то
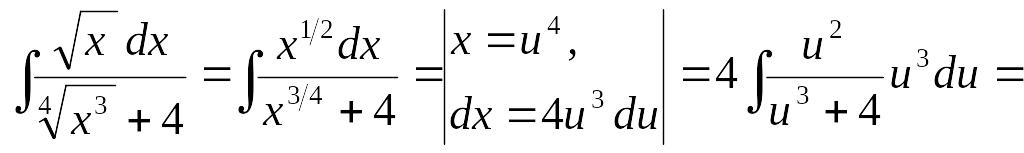
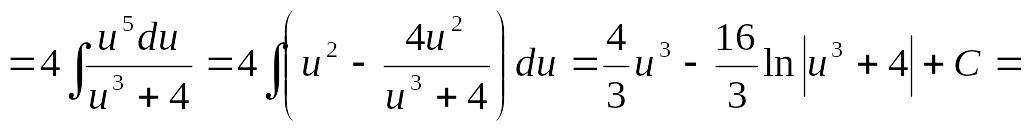
поскольку
.
Пример
14.
Найти
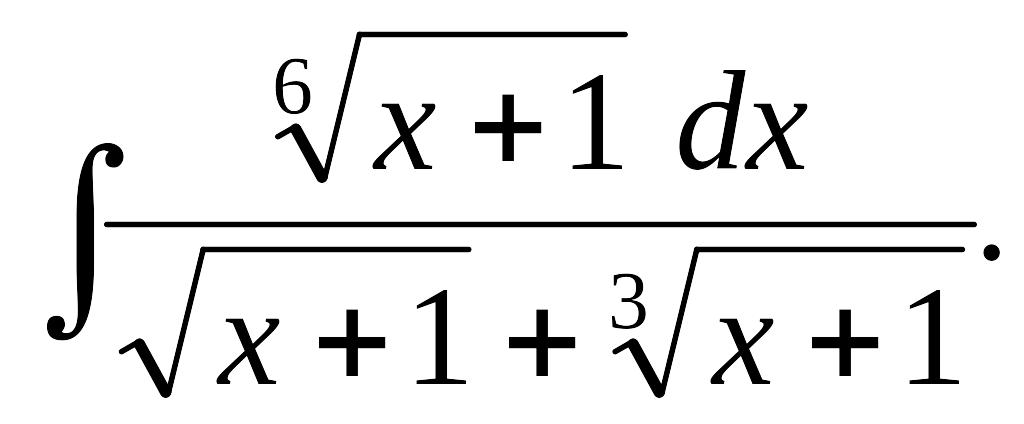
Так
как НОК (2,3,6) = 6, то
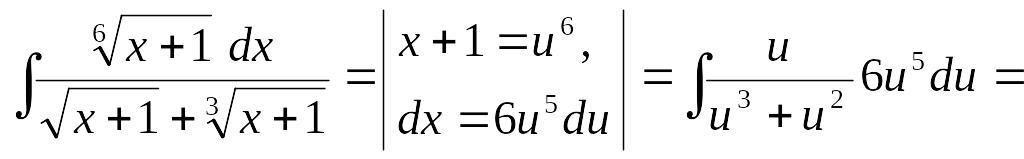
