Лекция 12. Интегральное исчисление Неопределенный интеграл

Функция F(x) называется первообразной функцией для функции f (x) на интервале (а,b), если F(x) дифференцируема на (а,b) и dF(x)=f(x)dx

.

(1)

Теорема. Если функция является первообразной функции на , то множество всех первообразных для задается формулой , где С – постоянное число.

Множество всех первообразных функций для называется неопределенным интегралом от функции и обозначается символом

,

(2)

где  - знак интеграла, - подынтегральная функция, - подынтегральное выражение, х - переменная интегрирования.

Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.

Геометрически неопределенный интеграл представляет собой семейство кривых (каждому числовому значению С соответствует определенная кривая семейства (рис.1). График каждой первообразной (кривой) называется интегральной кривой.

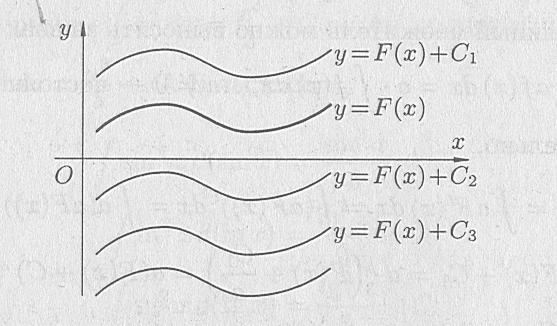
Рисунок 1

Основные свойства неопределенного интеграла

Если , то

1. 2. .

3. 4. .

5. .

6. Если , то и ,

где - произвольная функция, имеющая непрерывную производную.

Таблица неопределенных интегралов

1. 2.

3. 4.

5. 6.

7. 8.

9. 10.

11. 12.

13. 14.

15. 16.

17. 18.

19.

20. 21.

Правила интегрирования

Если , то

; ;

2. Методы интегрирования

Непосредственное интегрирование

Метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегрального выражения и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием.

Пример 1. ;

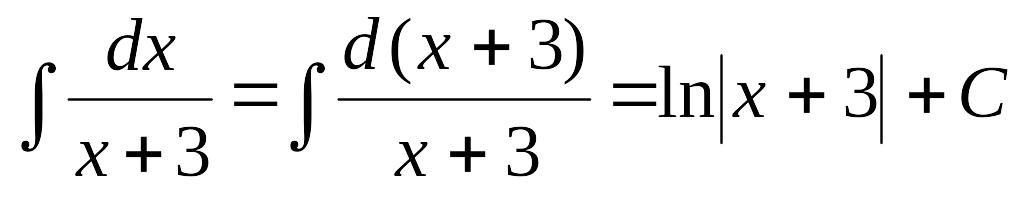Пример 2.

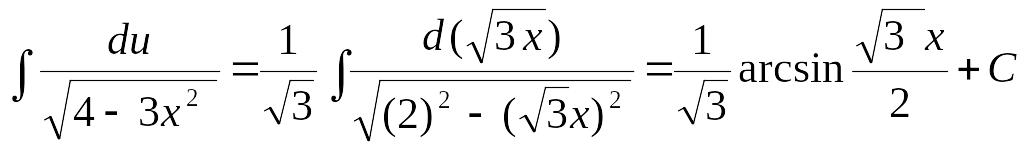
Метод подстановки (замены переменной)

Если заданная подынтегральная функция непрерывна на промежутке , то для замены перменной интегрирования по схеме

подбирается некоторая непрерывно дифференцируемая на соответствующем промежутке функция .

Так как , то формула замены переменной (подстановки) в неопределенном интеграле выглядит так:

.

(3)

Подстановка целесообразна лишь в том случае, когда интеграл в правой части по новой переменной t вычисляется легче по сравнению с заданным.

По определению дифференциала функции dφ(x).

Переход в этом равенстве слева направо называют «подведением под знак дифференциала». Это действие позволяет в несложных случаях применять метод подстановки без введения новой переменной интегрирования и найти неопределенный интеграл в виде сложной функции:

.

(4)

В частности, если функция, непрерывно дифференцируема на (а,b) и , то можем составить «логарифмический интеграл»

.

(5)

Пример 3. Найти .

Положим , тогда . Следовательно, .

Пример 4. Найти .

Пусть , тогда , поэтому

Пример 5. =