Частные производные высших порядков.

Частные производные и называют частными производными первого порядка. Их можно рассматривать как функции от .

Эти функции могут иметь частные производные, которые называются частными производными второго порядка.

Они определятся и обозначаются следующим образом:

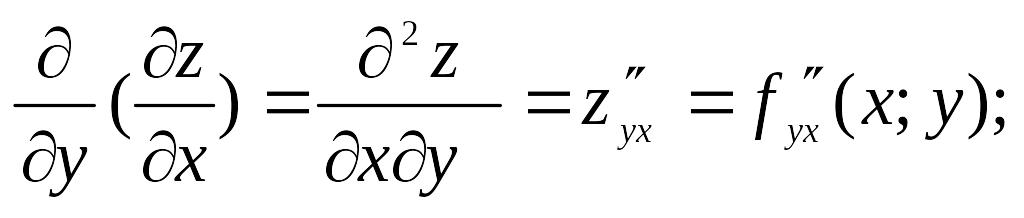
Аналогично определяется производные частные производные 3-го, 4-го и т.д. порядков. Так,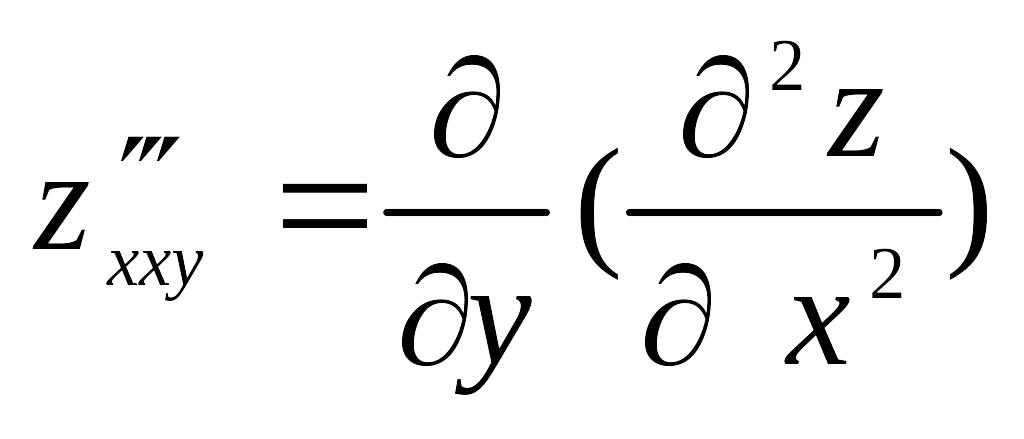 , и т. д.

Частная производная второго и более высокого порядка, взятая по различным переменным, называется смешанной частной производной. Таковыми являются, например .

Пример 4. Найти частные производные второго порядка функций .

Решение. , , . Оказа­лось, что . Этот результат не случаен. Имеет место теорема:

Теорема о смешанной производной (Шварца): Если частные производные высшего порядка непрерывны, то смешанные производные одного порядка, отличающиеся лишь порядком дифференцирования, равны между собой. В частности, для z = f(x,y) имеем:

Полный дифференциал функции

Пусть функция z=f(x,y) определена в некоторой окрестности точки M(x,y).

Составим полное приращение функции в точке М:

.

Функция z=f(x,y) называется дифференцируемой в точке M(x,y) ,если её полное приращение в этой точке можно представить в виде:

(1)

где и стремится к нулю при , . Сумма первых двух слагаемых в равенстве (1) представляет собой главную часть приращения.

Главная часть приращения, линейная относительно и , называется полным дифференциалом и обозначается символом:

(2)

Выражение называется частным дифференциалом. Для независимых переменных и полагают и . Тогда:

(3)

Теорема 1 (необходимое условие дифференцируемости функции):

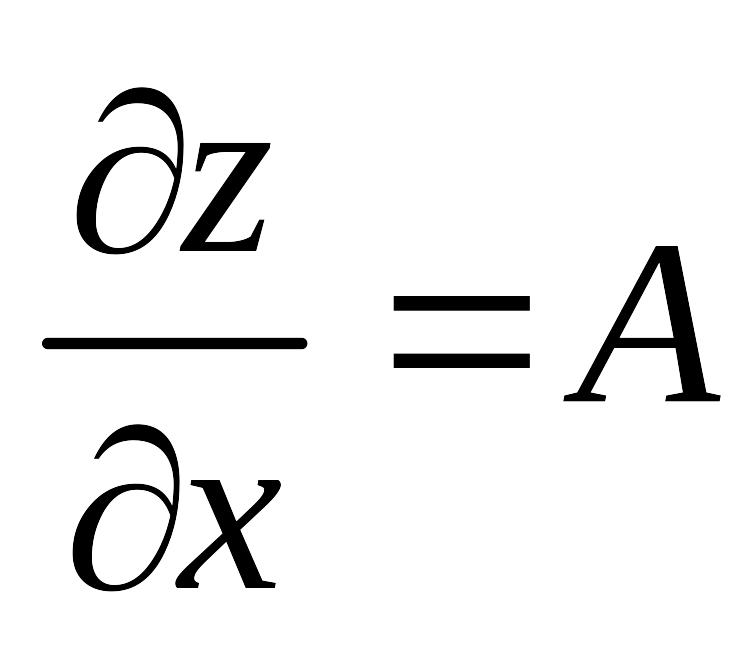Если функция z=f(x,y) дифференцируема в точке M(x,y) ,то она непрерывна в этой точке, имеет в ней частные производные и , причем и .

Теорема 2 (достаточное условие дифференцируемости функции): Если функция z=f(x,y) имеет непрерывные частные производные и в точке M(x,y), то она дифференцируема в этой точке и ее полный дифференциал выражается формулой:

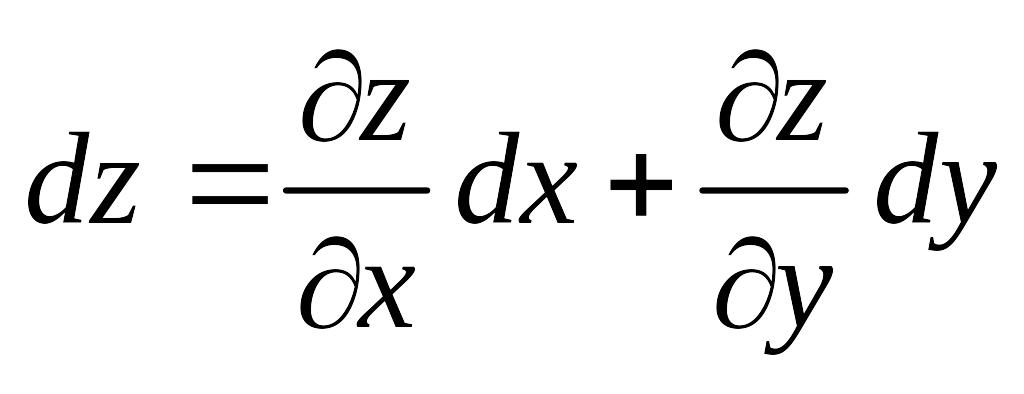или (4)

(5),

где и - частные дифференциалы функции z = f (x, y).

Применение полного дифференциала к приближенным вычислениям

Из определения дифференциала функции z=f(x,y) следует, что при достаточно малых | | и | | имеет место, приближенное равенство:

(6)

Отсюда имеем:

(7)

Этой формулой пользуются в приближенных расчетах.

Формула Тейлора

Приведем аналог формулы Тейлора для функции двух переменных. Если функция z =f(x,y) дифференцируема (n+1) раз в некоторой окрестности точки , то для каждой точки (x,y) из этой окрестности справедлива формула Тейлора

f(x.y) = f + + + +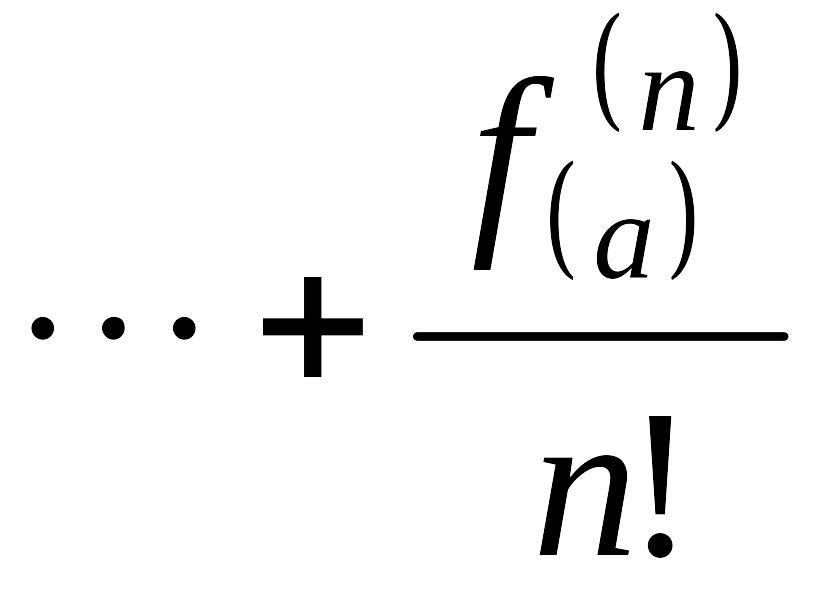r_n

Экстремум функции нескольких переменных

Пусть функция z =f(x,y) определена в некоторой области D,

Определение 1. Точка называется точкой максимума функции , если существует такая -окрестность точки , что для каждой точки (x,y) отличительной от точки из этой окрестности выполняется неравенство .

Определение 2. Точка называется точкой минимума функции , если существует такая -окрестность точки , что для каждой точки (x,y) отличительной от точки из этой окрестности выполняется неравенство .

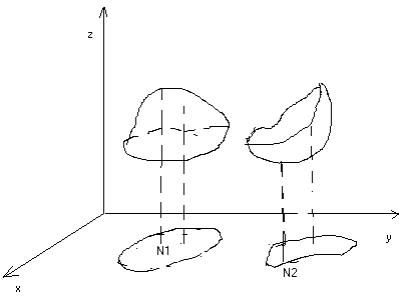
На рисунке 1 N₁ –точка максимума, N₂ –точка минимума.

Значение функции в точке максимума (минимума) называется макси­мумом (минимумом) функции. Максимум и минимум функции называют ее экстремумами.

Отметим, что в силу определения, точка экстремума функции лежит внутри области определения функции; максимум и минимум имеют локальный (местный) характер: значение функции в точке сравнивается с ее значениями достаточно близких к . В общем D функция может иметь несколько экстремумов или не иметь ни одного.