Асимптоты

Если график функции как угодно близко приближается к некоторой прямой, то такая прямая называется асимптотой функции.

Прямая называется вертикальной асимптотой графика непрерывной функции , если хотя бы один из односторонних пределов равен бесконечности

.

Как правило в точке а функция терпит разрыв 2 рода.

Прямая называется горизонтальной асимптотой (при ) к графику функции , если

Прямая называется наклонной асимптотой (при ) к графику функции , если , где

Теорема 6. Для того, чтобы прямая являлась наклонной асимптотой кривой , необходимо и достаточно, чтобы существовали конечные пределы:

.

(6)

Заметим, что прямая только при служит горизонтальной асимптотой. Если при , то кривая асимптот не имеет, например, парабола .

Общая схема исследования функции:

1. Исследуем функцию

1. найдем область определения функции;

2. четность;

3. периодичность;

4. точки пересечения с осями;

5. точки разрыва, поведение на бесконечности;

6. асимптоты.

2. Исследуем функцию

1) промежутки монотонности;

2) экстремумы.

3. Исследуем функцию

1) выпуклость вогнутость графика;

2) точки перегиба.

4. График.

Пример. Исследовать функцию

1. Исследуем функцию

1) , ;

2) , , т.е. функция четная;

3) непериодическая;

4) пересечение с осью ОХ: , ,

ОY: , ;

5. , ;

6. горизонтальная асимптота; наклонных асимптот нет.

2. .

,

точка максимума,

2. 

, точки перегиба.

График. Таким образом проведено полное исследование функции и построен её график.

Вопросы для самоконтроля:

1.Сформулируйте определение предела функции.

2.Сформулируйте определение предела последовательности.

3.Определение бесконечно малой и ее основные свойства.

4. Основные теоремы о пределах функций.

5. Первый замечательный предел.

6. Второй замечательный предел.

7.Сформулируйте определения непрерывности функции.

8. Какие точки называются точками разрыва функции?

9.Определение приращения аргумента и приращения функции.в точке х.

10.Определение непрерывной функции.

11.Определение производной функции у = f (х) в точке х.

12.Геометрический смысл производной.

13.Механический смысл производной.

14.Таблица производных.

15.Правила дифференцирования.

16. Производные сложной функции и обратной функций.

18. Дифференциал функции. Инвариантность его формы применения.

19. Производные высших порядков. Примеры.

20.Правило Лопиталя.

21.Производные функций, заданных параметрически.

22.Исследование функции.

Лекции 10 - 11. Функции нескольких переменных

(Определение функции нескольких переменных. Область определения функции многих переменных. Предел, непрерывность и дифференцируемость функции многих переменных. Частные производные, полный дифференциал функции многих переменных. Теорема о смешанной производной. Формула Тейлора. Экстремум функции нескольких переменных).

Функции нескольких переменных - естественное обобщение функций одной переменной. Рассмотрим функции двух переменных, т.к. во-первых, принципиального различия между двумя и большим числом переменных нет. Увеличение числа переменных ведет лишь к громоздкости выкладок. Во-вторых, случай двух переменных допускает наглядную геометрическую интерпретацию.

Пусть задано множество D упорядоченных пар чисел (x;y). Соответствие f, которое каждой пaре чисел (x;y)D сопоставляет одно и только одно число zR, называется функцией двух переменных, с областью определения D и областью значений в R, и записывается в виде z = f(x;y). Функцию z = f(x;y) часто записывают в виде: f: DR.

При этом x и y называются независимыми переменными (аргументами), а z - зависимой переменной (функцией).

Определение 1. Множество D=D(f) называется областью определения функции.

Определение 2. Множество значений, принимаемых Z в области определе­ния, называется областью изменения этой функции, обозначается E(f) или E.

Примером функции двух переменных может служить площадь S прямо­угольника со сторонами, длины которых равны x, y: S = x y. Областью опре­деления функции, является множество {(x; y)| x>0,y>0} .

Функцию z=f(x,y), где (x,y)D можно понимать как функцию точки M(x,y) координатной плоскости Oxy. В частности, областью определения может быть вся плоскость или ее часть, ограниченная некоторыми линями.

Определение 3. Линию, ограничивающую область, называют границей области.

Определение 4. Точки области, не лежащие на границе, называется внутренними.

Определение 5. Область, состоящая из одних внутренних точек, называется открытой.

Определение 6. Область с присоединенной к ней границей называется замкнутой. Значение функции z=f(x,y) в точке M₀(x₀; y₀) обозначают z₀ = f(x₀; y₀) или z₀=f(M₀) называют частными значениями.

Функция двух независимых переменных допускает геометрическое истол­кование. Каждой точке M₀(x₀; y₀) области в системе координат соответствует точка M₀(x₀; y₀; z₀), где z₀ = f (x₀; y₀) - аппликата точки М. Совокупность всех таких точек представляет собой некоторую поверхность, которая и будет геометрически изображать данную функцию z=f(x,y).

Пример 1. Функция имеет область определение круг и изображается верхней полусферой с центром в точке О(0;0;0) и радиусом R=1. (рисунок 1)

Функция двух переменных, как и функция одной переменной, может быть задана разными способами: таблицей, аналитически, графиком.

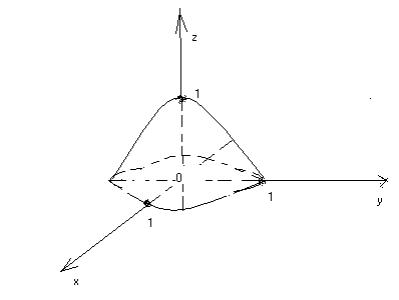
Рис. 1.

Предел функции двух переменных

Для функции двух (и большего числа) переменных вводится понятия предела функции и непрерывности, аналогично случаю функции одной переменной.

Введем понятие окрестности точки.

Определение 7. Множество всех точек M(x,y) плоскости, координаты которых удовлетворяют неравенству , называется

окрестностью точки M(x,y).

Другими словами, - окрестность точки Мо –это все внутренние точки с центром Мо и радиусом  (рисунок 2).

Пусть функция z = f(x,y) определена в некоторой окрестности точки Mо(xо;yо) ,кроме, быть может, самой этой точкой.

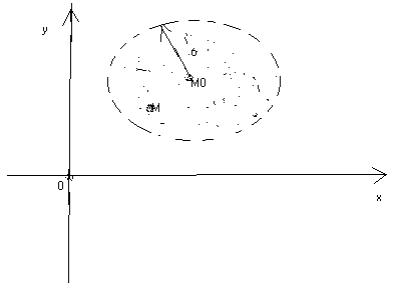Рис. 2.

Определение 8. Число называется пределом функции z = f(x,y) при и (или, что то ж самое, при M(x,y)  Mо(xо;yо)), если для и удовлетворяющих неравенству выполняется неравенство

Записывают:

Из определения следует, что если предел существует, то он не зависит от пу­ти, по которому М стремится к М₀ (число таких направлений бесконечно, для функции одной переменной ) по двум направлениям: справа и слева.

Геометрический смысл предела функции двух переменных состоит в следующем: Каково бы ни было число >0 ,  - окрестность точки

Mо(xо; yо), что во всех ее точках M(x,y), отличается от М₀, аппликат соответствующих точек поверхности z = f(x,y) отличаются от числа по модулю меньше чем на .

Предел функции двух переменных обладает свойствами, аналогичными свойствам предела функции одной переменной. Это означает, что справедливы утверждения: если функции и определены на множестве D и имеют в точке M₀ пределы соответственно, то и функции имеют в точке пределы, которые соответственно равны