Односторонние пределы

Если при стремлении х к а переменная х принимает значения, меньшие а, то такой предел называется левым и обозначается

(Обозначается или ).

Если же переменная х принимает только значения, большие а, то такой предел называется правым и обозначается

(Обозначается или ).

(Обозначается или )

Рисунок 21.

Пределы функции слева и справа наз. односторонними пределами

Теорема. существует в том и только в том случае, когда существуют пределы , и они равны между собой.

Основные теоремы о пределах.

Теорема 1. Предел суммы (разности) двух функций равен сумме (разности) их пределов:

Следствие. Функция может иметь только один предел при .

Теорема 2. Предел дроби равен пределу числителя, деленному на предел зна­менателя, если предел знаменателя не равен нулю:

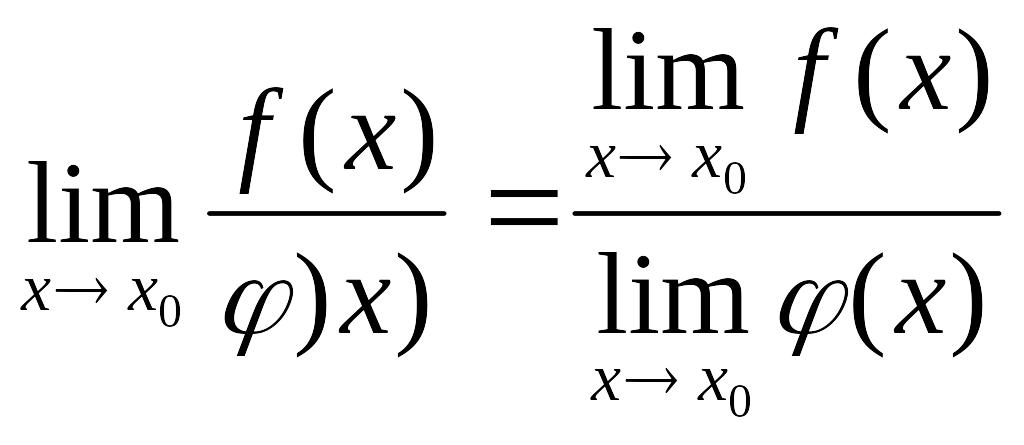
Теорема 3. Предел произведения двух функций равен произведению их пределов:

Следствие. Постоянный множитель можно выносить за знак предела:

Следствие. Предел степени с натуральным показателем равен той же степени предела

Бесконечно малые (б.м) и бесконечно большие (б.б) функции

Определение 4. Функция называется бесконечно малой (б. м.) при , если её предел равен нулю

Определение 5. Функция y=β(x) называется бесконечно большой (б.б.) при , если её предел при равен бесконечности

Пример 7.

Функция является б.м. при и не является таковой при .

Функция является б.б. функцией при

Теорема 1. Пусть — б.м. при , тогда их сумма также является б.м. при .

Теорема 2. Пусть б. м. при , а ограничена в некоторой окрестности точки а, тогда является б. м. при .

Если б.м. при и при то является б.б. при .

Бесконечно малые при называются эквивалентными, если . Обозначение .

Подобное определение дается и для б.б. функции.

Непрерывность функции

Определение 6. Функция называется непрерывной в точке х₀, если выполняются три условия:

1)существует (ф. определена в т. х ₀ )

2)существует конечный предел

3) .

Очевидно, что функция является непрерывной в точке в том и только в том случае, когда она непрерывна в этой точке слева и справа.

График непрерывной функции представляет из себя непрерывную линию.

Точка x₀, в которой нарушается хотя бы одно условие непрерывности функции , называется точкой разрыва этой функции.

Возможны три случая:

1. Если , то точка x₀ называется точкой разрыва первого рода функции .

2. Если хотя бы один из пределов не существует или равен бесконечности, то точка x₀ называется точкой разрыва второго рода функции .

3. Если не определена или , то x₀ называется точкой устранимого разрыва.

В простейших случаях нахождение предела сводится к подстановке в данное выражение предельного значения аргумента.

Часто, однако, подстановка предельного значения аргумента приводит к неопределенным выражениям вида , 0. ∞, 0⁰ , ∞⁰, 1^∞.

Нахождение предела функции в этих случаях называют раскрытием неопределенности.

Для раскрытия неопределенности вида , необходимо каждый член выражения разделить на х в старшей степени.

Для раскрытия неопределенности вида , прежде чем перейти к пределу, необходимо провести алгебраические преобразования, сократить дробь.

Для раскрытия неопределенности вида 0. ∞, ∞ - ∞, необходоимо при помощи тождественных преобразований свести их к одному из ранее рассмотренных случаев или .