Добавил:

A_ZCARD Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Российский химико-технологический университет им. Д.И. Менделеева

Предмет:

Математический анализ

Файл:

1 курс 2 семестр / Лекция 8

.pdf

Скачиваний:

Добавлен:

28.03.2020

Размер:

697.96 Кб

Скачать

☆

ЛЕКЦИЯ 8.

ДВОЙНОЙ ИНТЕГРАЛ: ОПРЕДЕЛЕНИЕ, ГЕОМЕТРИЧЕСКИЙ СМЫСЛ, ДОСТАТОЧНОЕ УСЛОВИЕ СУЩЕСТВОВАНИЯ, СВОЙСТВА, ТЕОРЕМА О СРЕДНЕМ ЗНАЧЕНИИ.

Двойной интеграл в декартовых координатах

Рассмотрим геометрическую задачу, приводящую к понятию двойного интеграла

Пусть на замкнутой области D		R² [область предполагаем

ограниченной и измеримой по Жордану. Мы не будем давать определение измеримости по Жордану, так как эти тонкие моменты выходят за рамки нашего курса. Данные определения можно посмотреть, например, в

прекрасном учебнике Г.И.Архипов, В.А. Садовничий, В.Н.Чубариков

«Лекции по математическому анализу», часть IV. Простыми словами,

измеримость по Жордану области означает возможность найти ее площадь,

для кривой – длину, для пространственной области - объем] задана непрерывная функция z f (x; y), f (x; y) 0 для (x; y) D . В системе координат 0xyz функция z f (x; y) задаёт некоторую поверхность z f (x; y

Из каждой граничной точки области D восстанавливаем перпендикуляры к плоскости 0xy до пересечения с поверхностью z f (x; y) . При этом в пространстве R³ получаем объёмное цилиндрическое тело, у которого нижним основанием является область D, верхним – часть поверхности

z f (x; y) и боковая поверхность параллельна оси 0z. Такое тело будем называть цилиндроидом.

Ставим задачу: вычислить объём V этого цилиндроида (рис. 1).

С этой целью проведём следующие операции:

а) область D разделим на n частей (произвольно) – D1, D2, D3,...,Dn;

[на самом деле не совсем произвольно. Полученные области должны быть измеримыми по Жордану.]

)

б) обозначим площади каждой из этих частей	S	, S	2	, S	,..., S			n	;
	1			3
в) на каждой из частей разбиения области D выберем точку						M	(x			;
						i		i

строим ряд цилиндрических «столбиков», имеющих основания Di

y )	и
i

и высоты

h f (M )		;
i	i

г) вычислим объёмы полученных «столбиков»:

V f (x ; y ) S ;
i	i	i	i

д) в результате построено тело, состоящее из n «столбиков», приближенно равное объёму цилиндроида, который равен:

	n	n	i	i	i
V	i		i	i	i
V	V		f (x ; y ) S			;
	i 1	i 1

е) для повышения точности равенства:

i 1

будем уменьшать размеры

частей разбиения области D, увеличивая их количество, т.е. n , но при

условии стремления к нулю max				S
условии стремления к нулю max				i , стягивающегося в точку. Тогда можно
записать точное равенство:
			n
V	lim		f (xi ; yi ) Si ;
	n		i 1
	max S	0	i 1
	max S	0
	i

ж) этот предел и даёт объём V заданного цилиндроида.

Замечание: проще всего начать с рассмотрения случая, когда область D –

прямоугольная. И разбивать ее на прямоугольники меньшего размера. Когда для такой области все станет понятно, то можно переходить к рассмотрению общего случая.

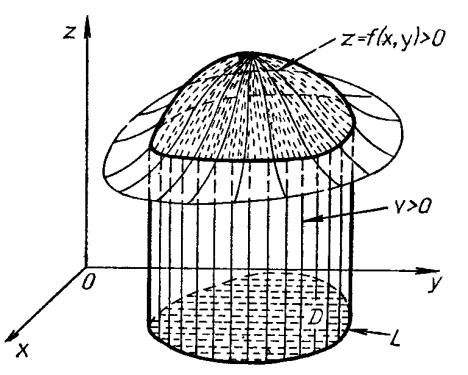
Рис. 1

Определение двойного интеграла

n Определение. Сумма f (xi ; yi ) Si , построенная в разделе 1 пункт д)

i 1

называется интегральной суммой для функции	f (x; y) на замкнутой области
D.
Определение. Двойным интегралом от функции f (x; y) по замкнутой

				n
области D называется предел интегральной суммы f (xi ; yi ) Si					при
				i 1
условиях:
а) n и			max	S
а) n и			max	i 0 (стягиваясь в точку);
б) этот предел существует и не зависит ни от способа разбиения области D на
части [измеримые по Жордану], ни от выбора внутри этих частей точек
M	(x ; y ) D .
i	i	i	i

Обозначение двойного интеграла:

					n	i	i	i
	f (x; y)dS		f (x; y)dxdy			i	i	i
	f (x; y)dS		f (x; y)dxdy	lim		f (x	; y	) S	.
D		D		n	i 1
D		D		max S 0	i 1
				max S 0
				i

Теорема (достаточное условие существования двойного интеграла)

Если в замкнутой области D		R² функция

двойной интеграл от этой функции по области

z f (x; y)

непрерывна, то

D существует.

Геометрический смысл двойного интеграла
1) Если функция z f (x; y) непрерывна в области D		R² и f(x;y) 0, то
1) Если функция z f (x; y) непрерывна в области D		R² и f(x;y) 0, то

двойной интеграл от этой функции по области D равен объёму цилиндроида,

у которого нижнее основание – область D Oxy , верхнее – часть поверхности z f (x; y) и боковая поверхность параллельна 0z (рис. 1), т.е.

Vцилиндроида f (x; y)dxdy

Если f(x;y) 0 в области D, то двойной интеграл численно равен объему цилиндрического тела, находящегося под плоскостью Oxy (рис. 2), взятому со знаком «–» (–V). Если же функция f(x,y) в области D меняет знак, то двойной интеграл численно равен разности объемов цилиндрических тел,

находящихся над плоскостью Oxy и под ней (рис. 3), т.е.

f (x, y)dS V1 V2 .

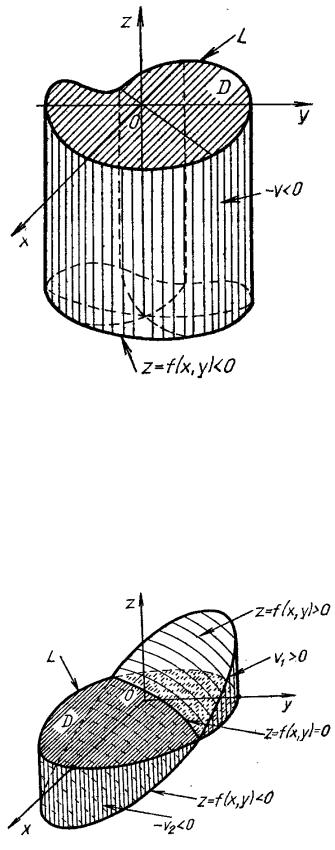
Рис. 2

2) Если

по области D

S	D		dxdy .
S			dxdy .
		D

Рис. 3

f (x; y)

равен

1	для любых	(x;
	для любых

площади области

, то двойной интеграл от z = 1

Основные свойства двойного интеграла

1) Пусть функция

f (x; y)

непрерывна в области D

R², причём

D1 D2	, тогда
f (x; y)dS f (x; y)dS f (x; y)dS.
	D	D
	1	2

Это свойство, как и последующие, можно доказать путём рассмотрения интегральных сумм и последующего перехода к пределам.

2) Постоянный множитель k выносится за знак двойного интеграла:

k f (x; y)dS k f (x; y)dS.
D	D

3) Двойной интеграл от суммы конечного числа функций равен сумме двойных интегралов от этих функций:

	1		2	(x; y) dS		1				2
	f	(x; y) f		(x; y) dS		f	(x; y)dS		f		(x; y)dS.
D					D			D

4) Если для двух непрерывных в области D функций f(x;y) и g(x;y)

выполняется неравенство f(x;y) g(x;y), то

f (x; y)dS D

g(x; y)dS D

Теорема (о среднем значении двойного интеграла)

	Если функция z f (x; y)		непрерывна в замкнутой области D, то внутри
области D найдется, хотя бы одна точка				0	0		, в которой выполняется
				(x	; y	)
равенство:
		f (x; y)ds f (x0 ; y0 ) SD ,
		D
где	S	D – площадь области D.
где		D – площадь области D.

Доказательство: По свойству непрерывной функции в замкнутой области,

функция z f (x; y) в области D достигает своих наименьшего (m) и

наибольшего (M) значений. Значит: m f(x;y) M для (x; y) D .

Тогда для всех (xi ; yi ) D можно записать

m f (xi ; yi ) M, где i 1; n.

Умножая последнее неравенство на

, получим:

m Si f (xi ; yi ) Si M Si .

Суммируем все n неравенств ( i 1; n ):

n	i	n	i i	i	n	i
	i		i i	i		i
	m S		f (x ; y ) S			M S	.
i 1		i 1			i 1

Вынесем пределам при

m lim Si

n i 1 max Si 0

m и М за знаки сумм (как постоянные величины) и перейдём к

n и max Si 0			(стягиваясь в точку):
		n		n
	lim	f (xi ; yi	) Si M lim	Si .
	n i 1		n i 1
	max S 0		max S 0
	i		i

Вспоминаем определение двойного интеграла, получаем двойное

неравенство:

m ds f (x; y)ds M ds
D	D	D
m SD f (x; y)ds M SD .
	D

Разделим последнее неравенство на

, где

. Тогда

m	f (x; y)ds
	D	M .

	S
	D
	По свойству непрерывной функции в замкнутой области, функция
z f (x; y)		в области D принимает все промежуточные значения между

наименьшим (m) и наибольшим (М) значениями. Следовательно, существует точка (x0 ; y0 ) D , в которой:

			f (x; y)ds				S D f (x; y)dS f (x0 ; y0 ) S D
f (x0	; y	0 )	D		,	умножаем на
			S
				D			D

Теорема доказана.

Геометрический смысл теоремы о среднем значении двойного интеграла

Если	f (x; y) 0	в области D, то объём цилиндроида V		f (x; y)dS

			D

можно заменить на объём цилиндра,

нижним будет область D, а высота f (

которого основаниями верхним и

0	.
; y )

Соседние файлы в папке 1 курс 2 семестр

#
28.03.2020444.39 Кб1Лекция 6.pdf
#
28.03.2020319.23 Кб1Лекция 7.pdf
#
28.03.2020697.96 Кб1Лекция 8.pdf
#
28.03.2020152.06 Кб3Первая КР.doc