
1 курс 2 семестр / Лекция 6
.pdfЛЕКЦИЯ 6.
ЭКСТРЕМУМЫ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Вжизни постоянно приходится сталкиваться с необходимостью принять наилучшее возможное решение. Огромное число подобных проблем возникает в экономике и технике. При этом часто случается так, что полезно прибегнуть к математике.
Вматематике исследование задач на максимум и минимум началось давно – двадцать пять веков назад. Долгое время к задачам на отыскание экстремумов не было единых подходов. Но примерно триста лет назад – в эпоху формирования математического анализа – были созданы первые общие методы решения и исследования задач на экстремум.
Накопление методов дифференциального исчисления приняло наиболее явную форму у Ферма. В 1638 году он сообщил в письме Декарту, что решил задачу определения экстремальных значений функции f (x) . Ферма нашел это условие алгебраическим путем. К
сожалению, Ферма не стремился публиковать свои работы, кроме того, пользовался труднодоступными для усвоения алгебраическими средствами Виета с его громоздкой символикой. Видимо, поэтому он не сделал последнего, уже небольшого, шага на пути к созданию дифференциального исчисления.
Накопление фактов дифференциального исчисления происходило быстро. В «Дифференциальном исчислении» (1755) Эйлера это исчисление появляется уже в весьма полном виде.
Правила определения экстремумов функции одной переменной y f (x) были даны Маклореном. Эйлер разработал этот вопрос для
функции двух переменных. Лагранж показал (1789), как отличать вид условного экстремума для функции многих переменных.
В XVIII веке возникло исчисление вариаций. В трудах Эйлера и Лагранжа оно приобрело вид логически стройной математической теории. Главной задачей, решаемой средствами этого исчисления, являются отыскание экстремумов функционалов.
Определение. Точка M 0 (x0 , y0 ) называется точкой минимума (максимума) функции z f (x, y) , если существует такая окрестность точки M 0 , что для всех точек M (x, y) из этой окрестности выполняется неравенство f (x0 , y0 ) f (x, y)
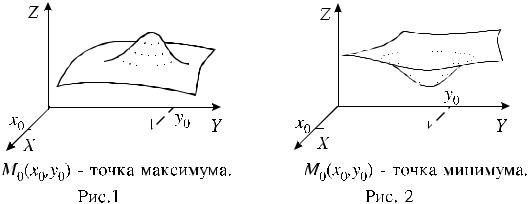
( f (x0 , y0 ) f (x, y) ).
Точки минимума и максимума функции |
z f |
экстремума, а значения функции в этих точках (минимумом и максимумом соответственно).
(
–
x, y) называются точками
экстремумами функции
Заметим, что минимум и максимум функции имеют локальный характер,
так как значение функции в точке |
M |
0 |
сравнивается с ее значениями в точках, |
|
достаточно близких к |
M |
0 . |
|
Теорема
экстремума
производные
(необходимое условие экстремума).
дифференцируемой функции |
z f ( |
|
|
в этой точке равны нулю: |
zx и z y |
||
Если x, y) ,
(x |
0 |
, y |
0 |
) |
|
|
|
то ее
– точка частные
z |
(x |
0 |
, y |
0 |
) 0, |
x |
|
|
|
z |
(x |
0 |
, y |
0 |
) |
y |
|
|
|
0
.
Точки, в которых частные производные первого порядка равны нулю, называются критическими или стационарными. В критических точках функция z f (x, y) может иметь экстремум, а может и не иметь.
Теорема (достаточное условие экстремума). Пусть функция |
z |
а) определена в некоторой окрестности критической точки которой
|
(x0 , y0 ) 0 |
и |
|
(x0 , y0 ) 0 |
; |
zx |
z y |
б) имеет непрерывные частные производные второго порядка
f
(x0
(
,
x, y) :
y0 ) , в
Тогда, если экстремум:
если AC B
|
z |
(x |
, y |
0 |
) |
A; z |
(x |
, y |
0 |
) B; z |
(x |
, y |
0 |
) C . |
|
|
xx |
0 |
|
|
xy |
0 |
|
yy |
0 |
|
|
|
|||
AC B |
2 |
0, то функция z f (x, y) в точке |
(x0 , y0 ) имеет |
||||||||||||
|
|||||||||||||||
|
максимум, если А<0; минимум, если А>0; |
|
|||||||||||||
2 |
0 |
, то функция z f (x, y) в точке |
(x0 , y0 ) экстремума не |
||||||||||||
|
|||||||||||||||
имеет. В случае открытым.
AC B |
2 |
0 |
|
|
вопрос о наличии экстремума остается
При исследовании функции двух переменных на экстремум рекомендуется использовать следующую схему:
1. |
Найти частные производные первого порядка: |
z |
и |
z . |
||||
|
|
|
|
|
|
x |
|
y |
|
|
|
x |
0, |
|
|
|
|
|
|
|
z |
|
|
|
|
|
2. |
Решить систему уравнений |
z |
0, |
и найти критические точки |
||||
|
|
|
|
|
|
|||
|
|
|
y |
|
|
|
|
|
функции.

3.
Найти частные производные второго порядка: z ,
xx
z xy
,
z yy
.
4.Вычислить значения частных производных второго порядка в каждой критической точке и, используя достаточные условия, сделать вывод
оналичии экстремума.
5.Найти экстремумы функции.
Пример 1. Найти экстремумы функции
z x |
3 |
y |
3 |
|
|
6xy
.
Решение. 1. Находим частные производные
z x
и |
z |
y
:
z x
3x2
6 y
,
z y
3y 2
6x
.
2. Для определения критических точек решаем систему уравнений
3x |
2 |
6 y 0, |
x |
2 |
2 y |
||
|
|
|
|||||
|
3y |
2 |
6x 0 |
или |
2 |
2x |
|
|
y |
||||||
|
|
|
|
|
|
||
Из первого уравнения системы находим: y x2
2
значение y во второе уравнение, получим
x |
4 |
|
|
|
|
|
|
2x 0 |
, x4 |
8x 0, x(x3 |
|
||
4 |
||||||
|
|
|
|
|||
откуда
x |
0, |
x |
2 |
2 |
. |
1 |
|
|
|
0,
0.
. Подставляя найденное
8) 0 |
, |

Находим значения
Подставляя значения
y1 |
0, |
y2 |
2. |
y, соответствующие значениям
x1 |
0, |
x2 |
2 |
в уравнение |
y |
x1
x |
2 |
|
|
|
, |
||
2 |
|||
|
|||
0, x2 2.
получим:
Таким образом, имеем две критические точки: |
M1 (0, |
3. Находим частные производные второго порядка:
|
|
|
|
|
|
|
|
|
|
zxx (3x |
2 |
6y)x |
6x ; |
zxy (3x |
2 |
6 y) y |
6 |
; |
z yy |
|
|
0)
(3
и
y |
2 |
|
M |
2 |
|
6
(2,
x) y
2)
.
6 y
.
4. Вычисляем значения частных производных второго порядка в каждой критической точке. Для точки M1 (0, 0) имеем:
A
Так как
z |
(0,0) |
xx |
|
0
AC
,
B z xy
B |
2 |
0 |
|
|
(0, 0) 6
0 ( 6) |
2 |
|
,
C
36
z |
(0, 0) |
yy |
|
0 |
, |
0
.
то в точке |
M |
1 |
экстремума нет. |
|
В точке |
M |
2 |
(2, 2) |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
A z |
|
(2, 2) 12 |
, B z |
(2, 2) 6 , |
C z |
(2, 2) |
12 |
|||||
|
|
|
xx |
|
|
|
xy |
|
|
|
yy |
|
|
|
и, следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
AC B |
2 |
12 12 |
( 6) |
2 |
144 |
36 108 0. |
|
||
|
|
|
|
|
|
|
||||||||
Значит, в силу достаточного условия существования экстремума, в точке
M |
2 |
функция имеет минимум, так как в этой точке 0 |
и A 0 . |
||
|
|||||
|
|
5. Находим значение функции в точке M 2 : |
|
||
|
|
z |
min |
z (2, 2) 23 23 6 2 2 8 . |
|
|
|
|
|
|
|
Ответ: zmin (2,2) 8 .

Пример 2. Исследовать функцию на экстремум
z 3x 2 y 2 6x 4 y 11.
Решение.
Найдем точки, возможного экстремума из необходимого условия
z |
0, |
z |
0 |
x |
|
y |
|
т.е.
z |
6x 6 |
6x 6 |
0 |
x |
|
||
z |
2 y 4 |
|
0 |
2 y 4 |
|||
y |
|
|
|
x 1 y 2
.
В точке (1,2) может быть экстремум. Теперь необходимо найти вторые производные:
|
6, |
|
0, |
|
2 . |
zxx |
zxy |
zyy |
Определитель
z |
| |
|
z |
| |
|
|
6 |
xx |
|
M |
xx |
|
M |
|
|
|
|
|
|
||||
z |
| |
M |
z |
| |
M |
|
0 |
xx |
|
xx |
|
|
|
0 |
12 |
|
2 |
||
|
0
.
Следовательно, экстремум есть, а так как минимума, т.е.
z xx
| |
M |
|
|
|
6
0
, то это точка
z |
min |
( 1,2) |
|
|
3 4 6 8 11
4
.
Ответ: zmin ( 1,2) 4 .

Пример 3. Исследовать на максимум и минимум следующую функцию
= + − − − , > .
Решение.
Найдем частные производные и :
= − − ,= − − .
= ,
Решим систему уравнений { = , которая в данном случае
− − = , |
− − = , |
||||
примет вид: { − − = , |
{ − − = , = , = , |
||||
− − = , − = , { = , |
{ = , |
{ = − , |
|||
|
|
= , |
= , |
= − , |
|
= , |
= − , |
|
|
|
|
{ = , и |
{ = − , |
не удовлетворяют условию > . |
|||
Получили точку возможного экстремума: ( ; )
Определим частные производные второго порядка:
|
|
= − , |
|
= − , |
|
|
= − . |
|||||
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||
Найдем значение ∆ в точке ( ; ): |
|
|
|
|||||||||
|
|
|
|
|
|
| = ′′ (; ) = , |
|
|||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| = ′′ (; ) = , |
|
||||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
= ′′ (; ) = −. |
|
|||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда |
|
|
|
|
|
|
|
|
|
|
||
|
∆= | |
|
− | = − (− ) = > |
|||||||||
|
|
− |
|
|
|
|
|
|
|
|||
и функция = + − − − в точке ( ; ) имеет экстремум.
Так как ′′ (; ) = > , то в точке ( ; ) функция
= + − − −
имеет минимум и
= (; ) = + − − ∙ ∙ − = − .
Ответ: ( ; ) - точка минимума, = − .
