Практична робота 6. Рішення задачі лінійного програмування симплекс-методом.

Мета: навчитись вирішувати задачу лінійного програмування.

Задача

Задана цільова функція:

при умовах:

Таблиця 6.1

Завдання

1. Значення всіх коефіцієнтів отримати згідно свого варіанту з таблиці 6.1

2. Вирішити симплекс-методом задачу лінійного програмування, використовуючи симплекс-таблиці.

Методичні вказівки

1. Перетворення стандартної форми задачі лінійного програмування в канонічну форму шляхом додавання невід'ємних змінних до кожної нерівності типу менше рівне (≤) обмежень:

2. Побудова і заповнення початкової симплекс таблиці. Симплекс таблиця є зручним інструментом для представлення канонічної форми лінійної задачі.Щоб заповнити початкову симплекс таблицю необхідно переписати цільову функцію F у вигляді аналогічному до системи обмежень, тобто:

Базис	План			...		...			...		MRT
F	0			...		...		0	...	0
				...		...		1	...	0
...
				...		...		0	...	0
				...		...		0	...

3. Перевірка на оптимальність. Якщо всі коефіцієнти в рядку F є невід'ємними, то отриманий розв'язок є оптимальним, якщо хоча б один коефіцієнт є від'ємний, то необхідно продовжити симплекс ітерацію (заповнити наступну симплекс таблицю).

4. Вибір ведучого стовпця. Ведучим називається стовпець в якому міститься найбільший за модулем від'ємний коефіцієнт в рядку F.

5. Вибір ведучого рядка та ведучого елемента , щоб вибрати ведучий рядок (а отже зміну, яка залишає базис) необхідно скористатись MRT тестом (мінімальне відношення). Для цього необхідно записати у відповідному рядку відношення змінної зі стовпця "план" до змінної з ведучого стовпця і визначити мінімальне з цих відношень. Рядок з мінімальним значенням з відношення буде ведучим рядком.

Зауваження: якщо коефіцієнт у ведучому стовпці рівний 0 або від'ємний, то у стовпці MRT ставиться нескінченність, тобто не враховується при виборі ведучого рядка; відношення не визначається для рядку F. На перетині ведучого стовпця та ведучого рядка знаходиться ведучий елемент .

6. Модифікація симплекс таблиці по відношенню до ведучого елемента .

   1. для ведучого рядка ---- ;

   2. для ведучого стовпця ---- ;

   3. для решти елементів ---- .

Згідно наведених правил здійснюється перерахунок елементів для нової симплекс таблиці.

7. Повернення до кроку 3.

Контрольні питання

1. Як будується симплекс-таблиця?

2. Як визначаються ключовий стовпець, рядок і число?

3. Як визначаються числа головного рядку?

4. Правила визначення похідних чисел.

5. Ознака оптимального рішення.

6. Що визначають в результаті рішення числа в стовпці вільних членів і число в клітинці індексного рядку стовпця вільних членів?

Література [1,3,5]

Практична робота 7. Рішення двоїстої задачі лінійного програмування

симплекс-методом.

Мета: навчитись вирішувати двоїсту задачу лінійного програмування.

Задача

Дані пр.роботи №6.

Завдання

1. Самостійно преобразовати задачу у двоїсту ЗЛП.

2. Вирішити симплекс-методом задачу лінійного програмування, використовуючи симплекс-таблиці.

Методичні вказівки

Для побудови двоїстої задачі необхідно звести пряму задачу до стандартного виду. Вважають, що задача лінійного програмування подана у стандартному вигляді, якщо для відшукання максимального значення цільової функції всі нерівності її системи обмежень приведені до виду « », а для задачі на відшукання мінімального значення — до виду « ».

Якщо пряма задача лінійного програмування подана в стандартному вигляді, то двоїста задача утворюється за такими правилами:

1. Кожному обмеженню прямої задачі відповідає змінна двоїстої задачі. Кількість невідомих двоїстої задачі дорівнює кількості обмежень прямої задачі.

2. Кожній змінній прямої задачі відповідає обмеження двоїстої задачі, причому кількість обмежень двоїстої задачі дорівнює кількості невідомих прямої задачі.

3. Якщо цільова функція прямої задачі задається на пошук найбільшого значення (max), то цільова функція двоїстої задачі — на визначення найменшого значення (min), і навпаки.

4. Коефіцієнтами при змінних у цільовій функції двоїстої задачі є вільні члени системи обмежень прямої задачі.

5. Правими частинами системи обмежень двоїстої задачі є коефіцієнти при змінних у цільовій функції прямої задачі.

6. Матриця

,

що складається з коефіцієнтів при змінних у системі обмежень прямої задачі, і матриця коефіцієнтів у системі обмежень двоїстої задачі

утворюються одна з одної транспонуванням, тобто заміною рядків стовпчиками, а стовпчиків — рядками.

Процес побудови двоїстої задачі зручно зобразити схематично:

Рис. 7.1. Схема побудови двоїстої задачі до прямої

Пари задач лінійного програмування бувають симетричні та несиметричні.

У симетричних задачах обмеження прямої та двоїстої задач є лише нерівностями, а змінні обох задач можуть набувати лише невід’ємних значень.

У несиметричних задачах деякі обмеження прямої задачі можуть бути рівняннями, а двоїстої — лише нерівностями. У цьому разі відповідні рівнянням змінні двоїстої задачі можуть набувати будь-яких значень, не обмежених знаком.

Всі можливі форми прямих задач лінійного програмування та відповідні їм варіанти моделей двоїстих задач у матричній формі наведено нижче.

Пряма задача	Двоїста задача
Cиметричні задачі
max F = CX AX   B X   0	min Z = BY ATY 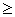  C Y   0
min F = CX AX   B X   0	max Z = BY ATY   C Y   0

Несиметричні задачі

max F = CX AX = B X   0	min Z = BY ATY   C Y
min F = CX AX = B X   0	max Z = BY ATY   C Y