Контрольні запитання:

1. Що означає абревіатура ЛПР?

2. Для чого потрібне дерево цілей?

3. Пояснить, як визначають загальне рішення згідно створеного дерева цілей?

4. За якими правилами формують матрицю парних порівнянь?

Література [5,6]

Практична робота №2. Найкоротший шлях на транспортній мережі.

Мета: набути практичні навички знаходження найкоротших відстаней зворотньою процедурою Беллмана.

Задача

Дана транспортна мережа (рис.2.1).

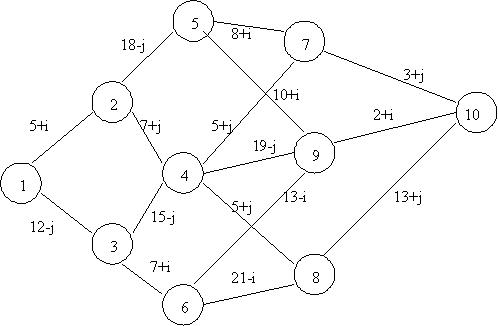
Рис. 2.1 Транспортна мережа

Завдання:

1. Відстані на малюнку розрахувати згідно свого варіанту.

2. Визначити найкоротшу відстань між 1 та 10 вершинами транспортної мережі.

Методичні вказівки

Кожен вид виробничої діяльності і може розглядатися як окремий крок оптимізації; безліч можливих значень перемінних (припустима область рішень) xі як варіанти рішень, а кількість кожного j-го виду ресурсу (B_i1,…, B_ij,… B_im), 0 B_ij b_j, доступного для розподілу на поточному і попередніх (або поточному і наступних) кроках (по і-м типах діяльності) як стан моделі. Тоді оптимальне значення цільової функції z для кроків і,і+1,...,n при заданих станах {Bіj} може бути записане у виді наступної рекуррентной функції Белмана (алгоритму прямого прогону):f_i(B_i1,…, B_{i m}) = max  {c_i x_i + f_i-1(B_i1-a_i1x_i ,…,B_{i m}-a_{i m}x_i )}, i =1,n;j =1,m, (1)

                                           0 a_ijx_i B_ij

с початковими умовами f₀(B₀₁,…,B_{0 m})=0.

Оптимальне значення цільової функції в зворотному часі для кроків n,..., і, і-1,...,1 при заданих станах {B_ij} може бути записане у виді наступного алгоритму зворотного прогону:

f_n(B_n1,…,B_nm)=max{c_nx_n},                              0 a_njx_n B_nj

f_i(B_i1,…,B_im)=max {c_ix_i+f_i+1(B_i1-a_i1x_i,…,B_{i m}-a_{i m}x_i)},i=1,n;j=1,m, 

                           0 a_ijx_i B_ij

де 0 B_ij b_j.

Різниця між прямим і зворотним способами рішення задачі полягає у визначенні стану моделі. У прямої моделі B/і j - кількість ресурсу j-го типу, що розподіляється від першого кроку до і-го, а для зворотної моделі Bіj- кількість ресурсу, що розподіляється на всіх кроках від і-го до n-го.

Рішення задачі ґрунтується на двох основних принципах.

Принципі інваріантного занурення, що визначає декомпозицію рішення загальної задачі на покрокове рішення часток (для кожного виду виробничої діяльності) задач, поєднуваних загальним ресурсом.

Принципі оптимальності, що визначає незалежність рішень, одержуваних на поточному кроці оптимізації, від рішень, отриманих на попередніх (наступних) кроках, а лише їх залежність від мети оптимізації і стану ресурсів на і-му кроці. При цьому гарантується оптимальність глобальної стратегії (послідовності рішень) при оптимальних локальних (покрокових) рішеннях.

Контрольні питання:

1. Особливості динамічного програмування

2. Які є різновиди методу Беллмана?

3. Які найкоротші відстані можна визначити по розрахованій таблиці методом Беллмана?

4. Як визначити послідовність вершин за методом Беллмана?

Література [1,7]

Практична робота №3. Найкоротший шлях на транспортній мережі.

Мета: набути практичні навички знаходження найкоротших відстаней методом метли

Задача

Дана транспортна мережа (рис.3.1).

Рис. 3.1 Транспортна мережа

Завдання:

1. Дати направлення ребрам графу транспортної мережі в напрямку від менших номерів вершин до більших номерів.

2. Відстані на малюнку розрахувати згідно свого варіанту.

3. Визначити найкоротшу відстань між 1 та 10 вершинами транспортної мережі.