Контрольні запитання:
Чому метод розв'язуючих доданків належить до групи методів умовно-оптимальних планів?
Коли доцільно використовувати цей метод рішення транспортної задачі лінійного програмування?
Що таке недостатня, достатня та нейтральна рядки?
Ознака оптимального рішення задачі?
Як оцінюють нейтральні рядки?
Як знаходять розв'язуючий доданок?
Для яких стовпчиків і як находять різницю?
Визначення загальної недостачі?
Література [1, 5]
Практична робота 13. Рішення незбалансованої транспортної задачі.
Мета: навчитись вирішувати незбалансовану транспортну задачу.
Задача
Дані роботи №8 (скореговані викладачем).
Завдання
1. Відстані та вантажообіг розрахувати згідно свого варіанту по таблиці 8.1
2. Скласти оптимальний план перевезень вантажів.
Методичні вказівки
Транспортна задача називається відкритою (незбалансованою) транспортною задачею, якщо умови балансу порушуються; у випадку виконання умови балансу вона називається збалансованою транспортною задачею.
Приведення відкритої транспортної задачі до збалансованої:
1. Перевищення запасів над потребами.
У цьому випадку вводиться "фіктивний" споживач з потребами рівними абсолютній величині різниці між загальною кількістю запасів і загальною кількістю необхідних одиниць. Вартість по доставці буде для споживача дорівнює 0, тому що постачання фактично немає.
2. Перевищення потреб над запасами.
Вводять "фіктивного" виробника (склад) з потребами рівними абсолютній величині різниці між загальною кількістю запасів і загальною кількістю необхідних одиниць. Вартість по доставці буде для виробника дорівнює 0, тому що постачання фактично немає.
Контрольні запитання:
Чим відрізняється збалансована ТЗ від незбалансованої?
Коли доцільно вводити фіктивного постачальника?
Коли доцільно вводити фіктивного споживача?
Ознака оптимального рішення задачі?
Література [1, 5]
Практична робота 14. Рішення транспортної задачі в сітьовій постановці.
Мета: навчитись вирішувати мережеву транспортну задачу.
Задача
Дані роботи №8 (скореговані викладачем).
Завдання
1. Відстані та вантажообіг розрахувати згідно свого варіанту по таблиці 8.1
2. Скласти оптимальний план перевезень вантажів.
Методичні вказівки
Якщо умови транспортної задачі задані у виді картосхеми, на якій умовно зображені постачальники, споживачі і дорогі, зазначені величини запасів вантажу і потреб у ньому, а також числа cіj - показники прийнятого в задачі критерію оптимальності (тарифи, відстані і т.п.), то говорять, що транспортна задача поставлена в мережній формі (рис. 14.1).
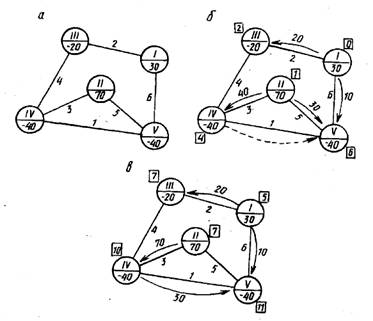
Рис. 14.1 Транспортна задача в мережевій постановці.
Описану картосхему називають транспортною мережею. Пункти розташування постачальників і споживачів зображують кружками і називають вершинами (вузлами) мережі, запаси вантажу записують в кружках позитивними, а потреби - негативними числами. Дороги, що зв'язують пункти розташування і споживання вантажу й інші пункти, зображують лініями і називають ребрами (дугами, ланками) мережі. При зображенні транспортної мережі реальний масштаб не дотримується. На мережі можуть бути зображені вершини, у яких немає ні постачальників, ні споживачів. Наявність таких вершин не вплине на спосіб рішення, якщо вважати, що запаси (потреби) вантажу в них дорівнюють нулю.
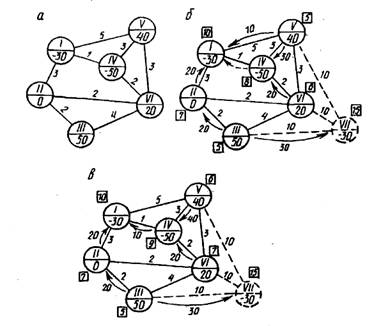
Рис.14.2 Приклад вирішення транспортної задачі в мережевій постановці
Такі вершини називають нульовими (див. вершину ІІ на рис. 13.2). Розходження між транспортними задачами в матричній і мережній формах дуже незначні, тому що методи їх рішення засновані на тих самих ідеях.
Постачання вантажу з вершини у вершину будемо позначати стрілками з указівкою величин постачань.
Рішення задачі на мережі починається з побудови початкового опорного плану.
Опорний план повинний задовольняти наступним вимогам:
1) всі запаси повинні бути розподілені, а потреби задоволені;
2) до кожної вершини повинна підходити чи виходити з її хоча б одна стрілка;
3) загальна кількість стрілок повинна бути на одиницю менше числа вершин;
4) стрілки не повинні утворювати замкнутий контур
Далі варто перевірити план на оптимальність.
Для цього обчислюють потенціали. Однієї з вершин (наприклад, вершині І) привласнимо деяке значення потенціалу (наприклад, рівне 0). (Для більшої наочності потенціали укладають у рамки.) Після цього, рухаючи по стрілках, визначають потенціали інших вершин, керуючись правилом: якщо стрілка виходить з вершини, то до потенціалу цієї вершини додаємо показник Cіj критерію оптимальності, якщо ж напрямок стрілки протилежний, то Cіj віднімаємо.
Після обчислення потенціалів знаходять характеристики ребер без стрілок за правилом: з більшого потенціалу віднімається менший, а різниця віднімається з показника Cіj, що відповідає даному ребру; якщо всі ребра без стрілок мають ненегативні характеристики, то складений план є оптимальним.
Якщо план неоптимальний.
Для поліпшення плану треба "завантажити" те ребро без стрілки, якому відповідає негативна характеристика. Якщо таких ребер трохи, то вибирається ребро з найбільшої по абсолютній величині негативною характеристикою і до нього підмальовується нова стрілка. При цьому утвориться замкнутий контур зі стрілок. Нова стрілка направляється від вершини з меншим потенціалом до вершини з великим потенціалом.
При визначенні величини постачання для ребра, що завантажується, розглядаються всі стрілки контуру, що утворився, (якщо на мережі - опорний план, то такий контур завжди існує, причому тільки один!), що мають напрямок, протилежний напрямку нової стрілки, і серед них знаходиться стрілка з найменшим постачанням - А. Обрана в такий спосіб величина додається до всіх постачань зі стрілками, що мають той же напрямок, що і нова стрілка, і віднімається з постачань у стрілках, що мають протилежний напрямок. Постачання в стрілках, що не входять у контур, зберігаються незмінними. Стрілка, по якій обране число А, ліквідується, і загальне число стрілок залишається колишнім.
Новий опорний план досліджується на оптимальність подібно попередньому. Практично зручніше вести розрахунки з позитивними числами, тому значення першого (обираного довільно) потенціалу краще брати рівним не нулю, а якому-небудь позитивному числу.
Виродження плану транспортної задачі в мережній постановці зовні виявляється в тім, що при повному використанні запасів і повному задоволенні потреб кількість стрілок виявляється менше, ніж n - 1, де n - загальне число вершин (включаючи і нульові!).
Спосіб подолання виродження дуже простий: додатково вводиться потрібна кількість стрілок з нульовими постачаннями. Напрямку стрілок вибираються довільно, однак вони не повинні утворювати замкнутий контур.
У випадку відкритої моделі уводять фіктивного споживача (постачальника) з попитом, рівним небалансу. Фіктивний споживач (постачальник) з'єднується ребрами безпосередньо з усіма постачальниками (споживачами). При цьому показники Cіj ребер, що з'єднують фіктивного споживача (постачальника) з постачальниками (споживачами), варто брати однаковими і порівняно великими. Робиться це для того, щоб виключити можливість використання фіктивної вершини як проміжний пункт.